二手车交易价格预测_Task4_建模与调参
import pandas as pd
import numpy as np
import warnings
warnings.filterwarnings('ignore') # 代码可以正常运行但是会提示警告,很烦人,有了这行代码就能忽略警告了
pd.set_option('display.max_columns', None) # 显示所有列
# 创建一个reduce_mem_usage函数,通过调整数据类型,减少数据在内存中占用的空间
def reduce_mem_usage(df):
'''
遍历DataFrame的所有列并修改它们的数据类型以减少内存使用
:param df: 需要处理的数据集
:return:
'''
start_mem = df.memory_usage().sum() # 记录原数据的内存大小
print('Memory usage of dataframe is{:.2f} MB'.format(start_mem))
for col in df.columns:
col_type = df[col].dtypes
if col_type != object: # 这里只过滤了object格式,如果代码中还包含其他类型,要一并过滤
c_min = df[col].min()
c_max = df[col].max()
if str(col_type)[:3] == 'int': # 如果是int类型的话,不管是int64还是int32,都加入判断
# 依次尝试转化成in8,in16,in32,in64类型,如果数据大小没溢出,那么转化
if c_min > np.iinfo(np.int8).min and c_max np.iinfo(np.int16).min and c_max np.iinfo(np.int32).min and c_max np.iinfo(np.int64).min and c_max np.finfo(np.float16).min and c_max np.finfo(np.float32).min and c_max < np.finfo(np.float32).max:
df[col] = df[col].astype(np.float32)
else:
df[col] = df[col].astype(np.float64)
else: # 如果不是数值型的话,转化成category类型
df[col] = df[col].astype('category')
end_mem = df.memory_usage().sum() # 看一下转化后的数据的内存大小
print('Memory usage after optimization is {:.2f} MB'.format(end_mem))
print('Decreased by {:.1f}%'.format(100 * (start_mem - end_mem) / start_mem)) # 看一下压缩比例
return df
# 读取我们为树模型准备的特征数据,并且将数据压缩
sample_feature = reduce_mem_usage(pd.read_csv(r'F:\Users\TreeFei\文档\PyC\ML_Used_car\data\data_for_tree.csv'))
Memory usage of dataframe is60507376.00 MB
Memory usage after optimization is 15724155.00 MB
Decreased by 74.0%
数据内存大小压缩了74%,看来效果拔群
# 把我们需要用的特征挑出(仅仅是列名,用来分离特征集和标签集)continuous_feature_names = [x for x in sample_feature.columns if x not in ['price', 'brand', 'model']]
# 处理一下sample_feature数据集的缺失值
sample_feature = sample_feature.dropna().replace('-', 0).reset_index(drop=True)
这里我比较疑惑为什么replace了’-’?
然后我看了看数据
sample_feature[sample_feature.isin(['-'])]
发现每非常多的样本都存在’-’,说明有一个特征里面有’-’
我第一时间考虑到了notRepairedDamage这个特征,因为它是唯一一个object类型的特征
sample_feature['notRepairedDamage']
果不其然,它是个类别特征,Categories (3, object): [-, 0.0, 1.0],有三个类别:’-’, ‘0’, ‘1’
# 既然想起来了notRepairedDamage不是数值型特征,那么我们把它转化一下sample_feature['notRepairedDamage'] = sample_feature['notRepairedDamage'].astype(np.float32)
# 处理完了之后,我们拿出我们挑选的特征和它的价格构造训练集
train = sample_feature[continuous_feature_names + ['price']]
train_X = train[continuous_feature_names]
train_y = train['price']
# 简单建模
from sklearn.linear_model import LinearRegression # 线性回归模型 y = wx + b
'''
这里比较疑惑,不是说用树模型嘛?挑的也是树模型的数据,为啥这里建了LR,看看再说
'''
model = LinearRegression(normalize=True) # normalize参数决定是否将数据归一化
model = model.fit(train_X, train_y)
# 查看训练的lR模型的截距(intercept)与权重(coef)
'intercept:' + str(model.intercept_)
'''
zip() - 可以将两个可迭代的对象,组合返回成一个元组数据
dict() - 使用元组数据构建字典
items方法 - items() 函数以列表返回可遍历的(键, 值) 元组数组
sort(iterable, cmp, key, reverse) - 排序函数
iterable - 指定要排序的list或者iterable
key - 指定取待排序元素的哪一项进行排序 - 这里x[1]表示按照列表中第二个元素排序
reverse - 是一个bool变量,表示升序还是降序排列,默认为False(升序)
'''
sorted(dict(zip(continuous_feature_names, model.coef_)).items(), key=lambda x: x[1], reverse=True)
# 这行代码返回了每个特征的权重,按照权重降序排列
import matplotlib.pyplot as plt
'''
np.random.randint() - 产生离散均匀分布的整数
取数范围:若high不为None时,取[low,high)之间随机整数,否则取值[0,low)之间随机整数
size - 54输出的大小,可以是整数也可以是元组
'''
subsample_index = np.random.randint(low=0, high=len(train_y), size=50) # 随机生成0-50000之间的50个整数
# 绘制v_9的值与标签的散点图
plt.scatter(train_X['v_9'][subsample_index], train_y[subsample_index], color='black')
plt.scatter(train_X['v_9'][subsample_index], model.predict(train_X.loc[subsample_index]), color='blue')
plt.xlabel('v_9')
plt.ylabel('price')
plt.legend(['True Price', 'Predicted'], loc='upper right')
print('The predicted price is obvious different from true price')
plt.show()
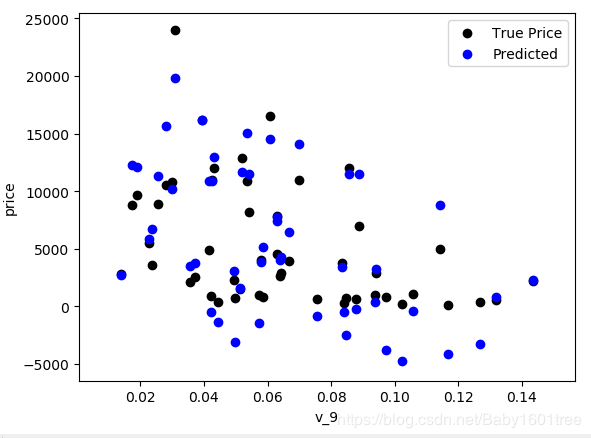
我们发现预测点和真实值差别较大,且有预测值出现了结果为负的情况,不符合实际情况,模型有问题
import seaborn as sns
print('It is clear to see the price shows a typical exponential distribution')
plt.figure(figsize=(15, 5))
plt.subplot(1, 2, 1)
sns.distplot(train_y)
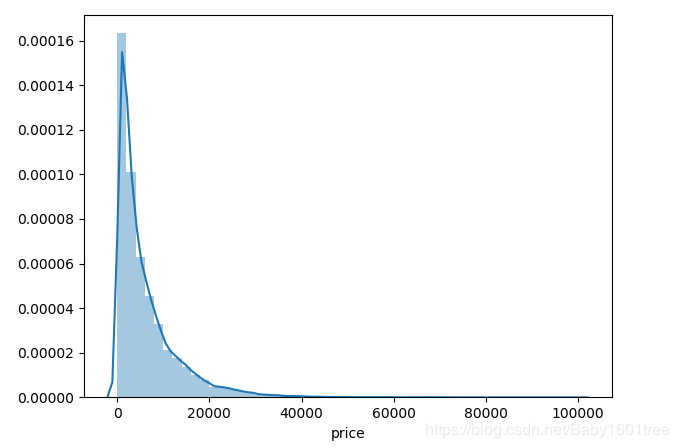
价格呈长尾分布,不利于建模预测,因为很多模型都假设数据误差项符合正态分布
plt.subplot(1, 2, 2)
'''
np.quantile(train_y, 0.9) - 求train_y 的90%的分位数
下面这个代码是把价格大于90%分位数的部分截断了,就是长尾分布截断
'''
sns.distplot(train_y[train_y < np.quantile(train_y, 0.9)])
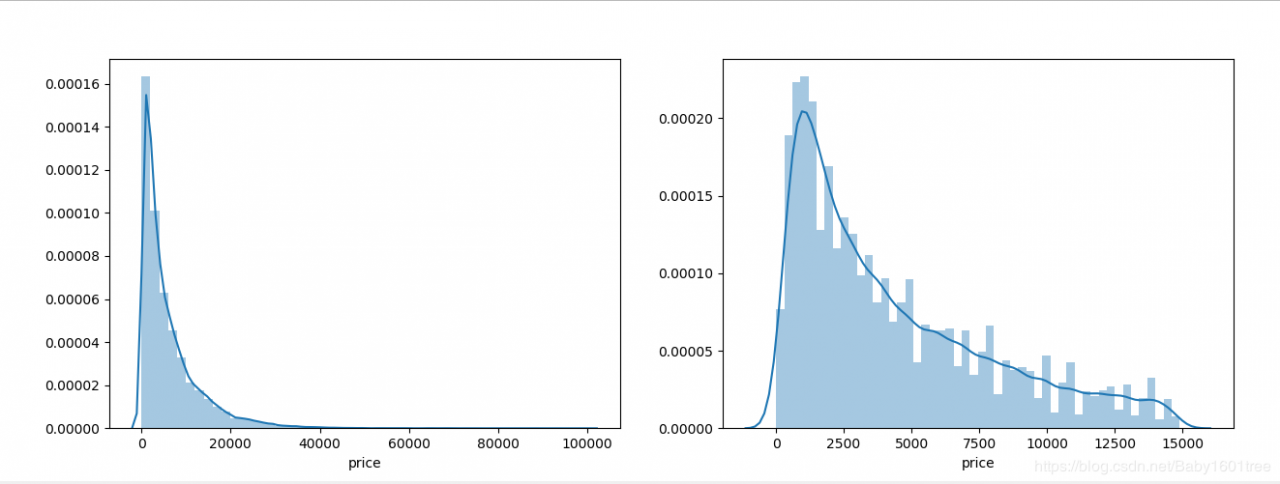
看上去好多了
train_y_In = np.log(train_y + 1)
print('The transformed price seems like normal distribution')
plt.figure(figsize=(15, 5))
plt.subplot(1, 2, 1)
sns.distplot(train_y_In)
plt.subplot(1, 2, 2)
sns.distplot(train_y_In[train_y_In < np.quantile(train_y_In, 0.9)])
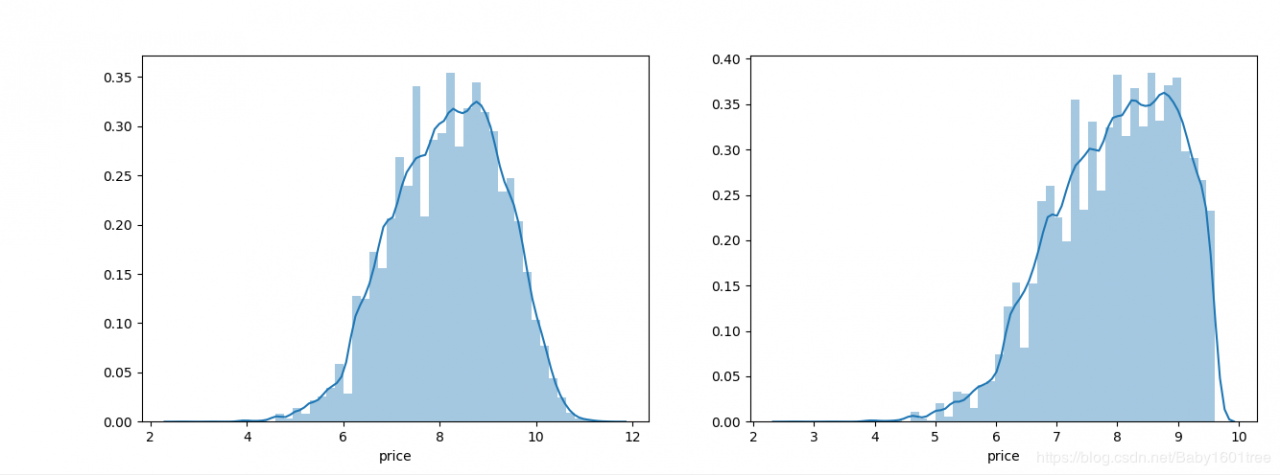
这回看上去像正态分布了,右边的图是做了长尾截断处理
model = model.fit(train_X, train_y_In)
print('intercept:' + str(model.intercept_))
sorted(dict(zip(continuous_feature_names, model.coef_)).items(), key=lambda x: x[1], reverse=True)
# 可视化一波,还是看v_9
plt.scatter(train_X['v_9'][subsample_index], train_y[subsample_index], color='black')
'''
np.exp() - 求e的幂次方,因为训练模型的时候log变换了,所以预测完了对比结果的时候得变回来
'''
plt.scatter(train_X['v_9'][subsample_index], np.exp(model.predict(train_X.loc[subsample_index])), color='blue')
plt.xlabel('v_9')
plt.ylabel('price')
plt.legend(['True Price', 'Predicted'], loc='upper right')
plt.show()
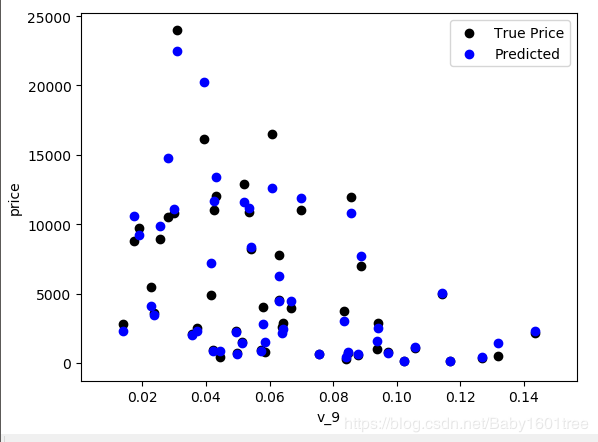
看上去准多了,预测值和真实值更加贴合
from sklearn.model_selection import cross_val_score
from sklearn.metrics import mean_absolute_error, make_scorer
定义一个函数,用来处理预测值和真实值的log变换
'''
numpy.nan_to_num(x) - 使用0代替数组x中的nan元素,使用有限的数字代替inf元素
'''
def log_transfer(func):
def warpper(y, yhat):
result = func(np.log(y), np.nan_to_num(np.log(yhat)))
return result
return warpper
# 我们使用线性回归模型,对未处理过标签的特征数据做5折交叉验证
scores = cross_val_score(model, X=train_X, y=train_y, verbose=1, cv=5,
scoring=make_scorer(log_transfer(mean_absolute_error)))
'''
verbose - 日志显示
verbose = 0 为不在标准输出流输出日志信息
verbose = 1 为输出进度条记录
verbose = 2 为每个epoch输出一行记录
make_scorer() - 工厂函数,自己定评分标准
这里的log_transfer()是返回log化的标签预测值和真实值
'''
print('AVG:', np.mean(scores))
— AVG: 1.3654295934396061 —> 5次的MAE平均值
# 我们再使用线性回归模型,对处理过标签的特征数据做5折交叉验证scores_In = cross_val_score(model, X=train_X, y=train_y_In, verbose=1, cv=5,
scoring=make_scorer(mean_absolute_error))
print('AVG:', np.mean(scores_In))
— AVG: 0.1932330179438017
MAE从1.365降低到0.193,误差缩小了很多
用2018年的二手车价格预测2017年是不合理的,所以我们可以用时间靠前的4/5样本当作训练集,靠后的1/5当验证集
import datetime # 这里我没看到datetime的作用,只能认为数据集是按照时间排列的
sample_feature = sample_feature.reset_index(drop=True) # 重置索引
split_point = len(sample_feature) // 5 * 4 # 设置分割点
train = sample_feature.loc[:split_point].dropna()
val = sample_feature.loc[split_point:].dropna()
train_X = train[continuous_feature_names]
train_y_In = np.log(train['price'] + 1)
val_X = val[continuous_feature_names]
val_y_In = np.log(val['price'] + 1)
model = model.fit(train_X, train_y_In)
mean_absolute_error(val_y_In, model.predict(val_X))
— MAE为0.196,和五折交叉验证差别不大
# 绘制学习率曲线与验证曲线from sklearn.model_selection import learning_curve, validation_curve
创建绘制学习率曲线的函数
def plot_learning_curve(estimator, title, X, y, ylim=None, cv=None, n_jobs=1, train_sizes=np.linspace(.1, 1.0, 5)):
plt.figure()
plt.title(title)
if ylim is not None:
plt.ylim(*ylim) # 如果规定了ylim的值,那么ylim就用规定的值
plt.xlabel('Training example')
plt.ylabel('score')
train_size, train_scores, test_scores = learning_curve(estimator, X, y, cv=cv, n_jobs=n_jobs,
train_sizes=train_sizes,
scoring=make_scorer(mean_absolute_error))
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
test_scores_std = np.std(test_scores, axis=1)
plt.grid()
'''
fill_between()
train_sizes - 第一个参数表示覆盖的区域
train_scores_mean - train_scores_std - 第二个参数表示覆盖的下限
train_scores_mean + train_scores_std - 第三个参数表示覆盖的上限
color - 表示覆盖区域的颜色
alpha - 覆盖区域的透明度,越大越不透明 [0,1]
'''
plt.fill_between(train_sizes, train_scores_mean - train_scores_std,
train_scores_mean + train_scores_std, alpha=0.1, color='r')
plt.fill_between(train_sizes, test_scores_mean - test_scores_std,
test_scores_mean + test_scores_std)
plt.plot(train_sizes, train_scores_mean, 'o-', color='r', label='Training score')
plt.plot(train_sizes, test_scores_mean, 'o-', color='g', label='Cross-validation score')
plt.legend(loc='best')
return plt
plot_learning_curve(LinearRegression(), 'Liner_model', train_X[:1000], train_y_In[:1000],
ylim=(0.0, 0.5), cv=5, n_jobs=1)
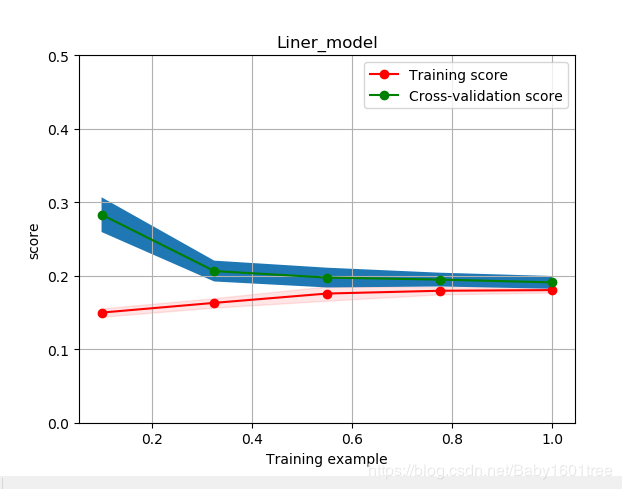
模型在训练集拟合的不错,在验证集中表现一般
1.L1正则化 - Lasso回归 -
模型被限制在正方形区域(二维区域下),损失函数的最小值往往在正方形(约束)的角上,很多权值为0(多维),所以可以实现模型的稀疏性(生成稀疏权值矩阵,进而用于特征选择
2.L2正则化 - 岭回归 -
模型被限制在圆形区域(二维区域下),损失函数的最小值因为圆形约束没有角,所以不会使得权重为0,但是可以使得权重都尽可能的小,最后得到一个所有参数都比较小的模型,这样模型比较简单,能适应不同数据集,一定程度上避免了过拟合
from sklearn.linear_model import Ridge
from sklearn.linear_model import Lasso
models = [LinearRegression(), Ridge(), Lasso()]
result = dict() # 创建一个用来装结果的字典
for model in models:
model_name = str(model).split('(')[0] # 把括号去掉,只保留名字
scores = cross_val_score(model, X=train_X, y=train_y_In, verbose=0, cv=5, # 五折交叉验证
scoring=make_scorer(mean_absolute_error))
result[model_name] = scores
print(model_name + ' is finished')
result = pd.DataFrame(result)
result.index = ['cv' + str(x) for x in range(1, 6)]
result
model_Lr = LinearRegression().fit(train_X, train_y_In)
print('intercept:' + str(model_Lr.intercept_))
sns.barplot(abs(model_Lr.coef_), continuous_feature_names)
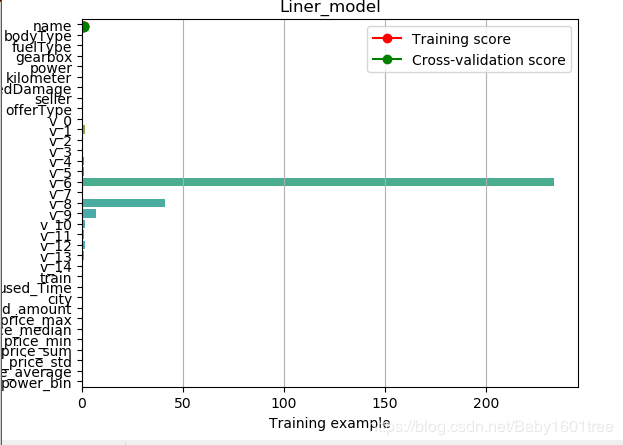
— 线性回归模型:发现v_6, v_8, v_9权重大
model_Ridge = Ridge().fit(train_X, train_y_In)
print('intercept:' + str(model_Ridge.intercept_))
sns.barplot(abs(model_Ridge.coef_), continuous_feature_names)
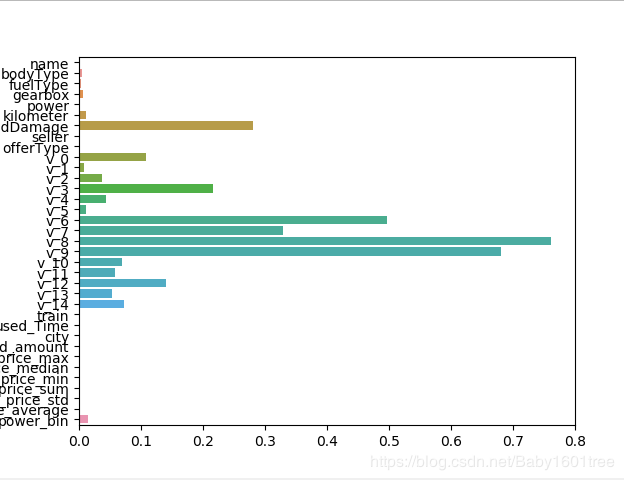
— 岭回归:发现有更多的参数对模型起到影响,而且参数都比较小,一定程度上避免了过拟合现象,抗扰动能力强
model_Lasso = Lasso().fit(train_X, train_y_In)
print('intercept:' + str(model_Lasso.intercept_))
sns.barplot(abs(model_Lasso.coef_), continuous_feature_names)
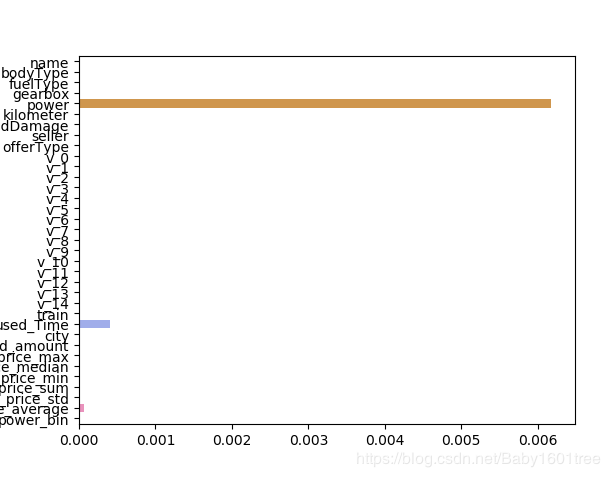
— lasso回归:发现power和used_time这两个特征很重要,L1正则化有助于生成一个稀疏权值矩阵,进而用于特征选择
'''
SVM - 支持向量机 - 通过寻求结构化风险最小来提高学习机泛化能力,基本模型定义为特征空间上的间隔最大的线性分类器
支持向量机的学习策略便是间隔最大化
SVR - 用于标签连续值的回归问题
SVC - 用于分类标签的分类问题
'''
from sklearn.svm import SVC # 这里用SVR是不是好得多?
from sklearn.tree import DecisionTreeRegressor # 决策树回归
from sklearn.ensemble import RandomForestRegressor # 随机森林回归
'''
Boosting算法思想 - 一堆弱分类器的组合就可以成为一个强分类器;
不断地在错误中学习,迭代来降低犯错概率
通过一系列的迭代来优化分类结果,每迭代一次引入一个弱分类器,来克服现在已经存在的弱分类器组合的短板
Adaboost - 整个训练集上维护一个分布权值向量W
用赋予权重的训练集通过弱分类算法产生分类假设(基学习器)y(x)
然后计算错误率,用得到的错误率去更新分布权值向量w
对错误分类的样本分配更大的权值,正确分类的样本赋予更小的权值
每次更新后用相同的弱分类算法产生新的分类假设,这些分类假设的序列构成多分类器
对这些多分类器用加权的方法进行联合,最后得到决策结果
Gradient Boosting - 迭代的时候选择梯度下降的方向来保证最后的结果最好
损失函数用来描述模型的'靠谱'程度,假设模型没有过拟合,损失函数越大,模型的错误率越高
如果我们的模型能够让损失函数持续的下降,最好的方式就是让损失函数在其梯度方向下降
GradientBoostingRegressor()
loss - 选择损失函数,默认值为ls(least squres),即最小二乘法,对函数拟合
learning_rate - 学习率
n_estimators - 弱学习器的数目,默认值100
max_depth - 每一个学习器的最大深度,限制回归树的节点数目,默认为3
min_samples_split - 可以划分为内部节点的最小样本数,默认为2
min_samples_leaf - 叶节点所需的最小样本数,默认为1
参考资料:https://www.cnblogs.com/zhubinwang/p/5170087.html
'''
from sklearn.ensemble import GradientBoostingRegressor
'''
MLPRegressor - 人工神经网络,了解的不多
参数详解
hidden_layer_sizes - hidden_layer_sizes=(50, 50),表示有两层隐藏层,第一层隐藏层有50个神经元,第二层也有50个神经元
activation - 激活函数 {‘identity’, ‘logistic’, ‘tanh’, ‘relu’},默认relu
identity - f(x) = x
logistic - 其实就是sigmod函数,f(x) = 1 / (1 + exp(-x))
tanh - f(x) = tanh(x)
relu - f(x) = max(0, x)
solver - 用来优化权重 {‘lbfgs’, ‘sgd’, ‘adam’},默认adam,
lbfgs - quasi-Newton方法的优化器:对小数据集来说,lbfgs收敛更快效果也更好
sgd - 随机梯度下降
adam - 机遇随机梯度的优化器
alpha - 正则化项参数,可选的,默认0.0001
learning_rate - 学习率,用于权重更新,只有当solver为’sgd’时使用
max_iter - 最大迭代次数,默认200
shuffle - 判断是否在每次迭代时对样本进行清洗,默认True,只有当solver=’sgd’或者‘adam’时使用
'''
from sklearn.neural_network import MLPRegressor
'''
XGBRegressor - 梯度提升回归树,也叫梯度提升机
采用连续的方式构造树,每棵树都试图纠正前一棵树的错误
与随机森林不同,梯度提升回归树没有使用随机化,而是用到了强预剪枝
从而使得梯度提升树往往深度很小,这样模型占用的内存少,预测的速度也快
'''
from xgboost.sklearn import XGBRegressor
from lightgbm.sklearn import LGBMRegressor
models = [LinearRegression(), DecisionTreeRegressor(), RandomForestRegressor(),
GradientBoostingRegressor(), MLPRegressor(solver='lbfgs', max_iter=100),
XGBRegressor(n_estimators=100, objective='reg:squarederror'),
LGBMRegressor(n_estimators=100)]
result = dict()
for model in models:
model_name = str(model).split('(')[0]
scores = cross_val_score(model, X=train_X, y=train_y_In,
verbose=0, cv=5, scoring=make_scorer(mean_absolute_error))
result[model_name] = scores
print(model_name + ' is finished')
result = pd.DataFrame(result)
result.index = ['cv' + str(x) for x in range(1, 6)]
result
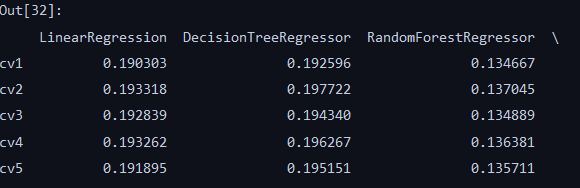
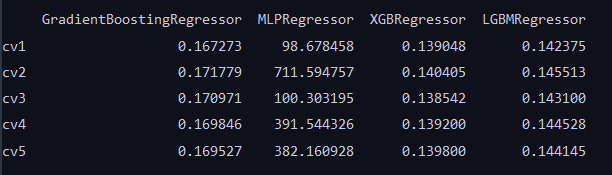
整体看来,随机森林在每一折的表现最好,XGB也不错,LGB最小值在0.143左右
''''
LightGBM - 使用的是histogram算法,占用的内存更低,数据分隔的复杂度更低
思想是将连续的浮点特征离散成k个离散值,并构造宽度为k的Histogram
然后遍历训练数据,统计每个离散值在直方图中的累计统计量
在进行特征选择时,只需要根据直方图的离散值,遍历寻找最优的分割点
LightGBM采用leaf-wise生长策略:
每次从当前所有叶子中找到分裂增益最大(一般也是数据量最大)的一个叶子,然后分裂,如此循环。
因此同Level-wise相比,在分裂次数相同的情况下,Leaf-wise可以降低更多的误差,得到更好的精度
Leaf-wise的缺点是可能会长出比较深的决策树,产生过拟合
因此LightGBM在Leaf-wise之上增加了一个最大深度的限制,在保证高效率的同时防止过拟合
'''
'''
参数:
num_leaves - 控制了叶节点的数目,它是控制树模型复杂度的主要参数,取值应 <= 2 ^(max_depth)
bagging_fraction - 每次迭代时用的数据比例,用于加快训练速度和减小过拟合
feature_fraction - 每次迭代时用的特征比例,例如为0.8时,意味着在每次迭代中随机选择80%的参数来建树,
boosting为random forest时用
min_data_in_leaf - 每个叶节点的最少样本数量。
它是处理leaf-wise树的过拟合的重要参数
将它设为较大的值,可以避免生成一个过深的树。但是也可能导致欠拟合
max_depth - 控制了树的最大深度,该参数可以显式的限制树的深度
n_estimators - 分多少颗决策树(总共迭代的次数)
objective - 问题类型
regression - 回归任务,使用L2损失函数
regression_l1 - 回归任务,使用L1损失函数
huber - 回归任务,使用huber损失函数
fair - 回归任务,使用fair损失函数
mape (mean_absolute_precentage_error) - 回归任务,使用MAPE损失函数
'''
## 贪心算法
– LGB的参数集合
objective = ['regression', 'regression_l1', 'mape', 'huber', 'fair']
num_leaves = [3, 5, 10, 15, 20, 40, 55]
max_depth = [3, 5, 10, 15, 20, 40, 55]
bagging_fraction = []
feature_fraction = []
drop_rate = []
贪心调参
'''
建立数学模型来描述问题
把求解的问题分成若干个子问题
对每个子问题求解,得到子问题的局部最优解
把子问题的解局部最优解合成原来问题的一个解
总是做出在当前看来是最好的选择,也就是说,不从整体最优上加以考虑,它所做出的仅仅是在某种意义上的局部最优解
对于一个具体问题,要确定它是否具有贪心选择性质,必须证明每一步所作的贪心选择最终导致问题的整体最优解
'''
# 局部最优解 - objective
best_obj = dict()
for obj in objective:
model = LGBMRegressor(objective=obj)
score = np.mean(cross_val_score(model, X=train_X, y=train_y_In, verbose=0,
cv=5, scoring=make_scorer(mean_absolute_error)))
best_obj[obj] = score
# 局部最优解 - num_leaves --- 此时得限制objective参数,得是mae值最小,即误差最小的那个问题类型
best_leaves = dict()
for leaves in num_leaves:
'''
best_obj.items() - 把best_obj字典中的元组装进列表
key=lambda x: x[1] - 取前一个对象的第二维的数据,即原字典的value值
min(best_obj.items(), key=lambda x: x[1]) - 选择best_obj中value值最小的那组元组
min(best_obj.items(), key=lambda x: x[1])[0] - 返回value值最小的key,即问题类型objective
'''
model = LGBMRegressor(objective=min(best_obj.items(), key=lambda x: x[1])[0], num_leaves=leaves)
score = np.mean(cross_val_score(model, X=train_X, y=train_y_In, verbose=0,
cv=5, scoring=make_scorer(mean_absolute_error)))
best_leaves[leaves] = score
# 局部最优解 - max_depth --- 此时得限制objective参数和num_leaves参数,都得是mae值的问题类型和叶节点数
best_depth = dict()
for depth in max_depth:
model = LGBMRegressor(objective=min(best_obj.items(), key=lambda x: x[1])[0],
num_leaves=min(best_leaves.items(), key=lambda x: x[1])[0],
max_depth=depth)
score = np.mean(cross_val_score(model, X=train_X, y=train_y_In, verbose=0,
cv=5, scoring=make_scorer(mean_absolute_error)))
best_depth[depth] = score
经过漫长的等待…
以上就是贪心算法的思想:局部求得最优解之后,固定条件再求别的局部最优解,最后得出所有局部最优的参数
sns.lineplot(x=['0_initial', '1_turning_obj', '2_turning_leaves', '3_turning_depth'],
y=[0.143, min(best_obj.values()), min(best_leaves.values()), min(best_depth.values())])
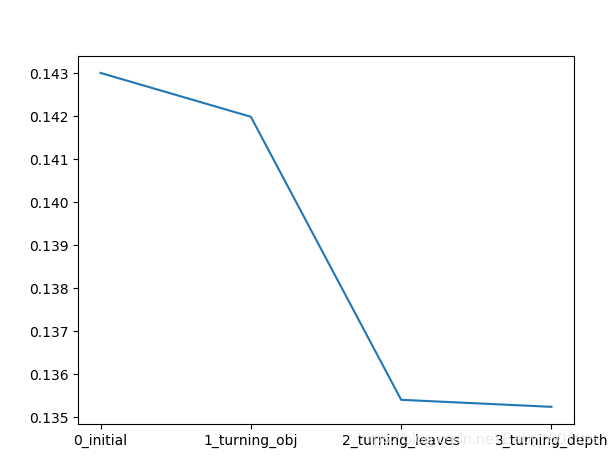
能看出,XGB模型在没有调参的情况下,MAE约0.143
局部选择最优objective参数后,MAE下降约为0.142
再选择了最优的best_leaves参数后,MAE为0.1354左右(优化了很多)
最后选择了best_depth参数后,MAE为0.1353左右,差别不大
'''
通过循环遍历,尝试每一种参数组合,返回最好的得分值的参数组合
GridSearchCV能够使我们找到范围内最优的参数,param_grid参数越多,组合越多,计算的时间也需要越多
GridSearchCV适用于小数据集
'''
from sklearn.model_selection import GridSearchCV
parameters = {'objective': objective, 'num_leaves': num_leaves, 'max_depth': max_depth} # 给定参数取值范围
model = LGBMRegressor() # 创建实例
clf = GridSearchCV(model, parameters, cv=5) # 网格搜索,遍历各种特征组合,五折交叉验证
clf = clf.fit(train_X, train_y_In) # 训练的过程的确很缓慢,超级慢
clf.best_params_
# 结果Out[10]: {'max_depth': 10, 'num_leaves': 55, 'objective': 'huber'},和教材不一样
model = LGBMRegressor(objective='huber', num_leaves=55, max_depth=15)
np.mean(cross_val_score(model, X=train_X, y=train_y_In, verbose=0, cv=5, scoring=make_scorer(mean_absolute_error)))
Out[36]: 0.1370086509753757
MAE为0.137
结果Out[10]: {‘max_depth’: 10, ‘num_leaves’: 55, ‘objective’: ‘huber’},和教材不一样
'''
贝叶斯优化是一种用模型找到函数最小值方法
贝叶斯方法与随机或网格搜索的不同之处在于:它在尝试下一组超参数时,会参考之前的评估结果,因此可以省去很多无用功
贝叶斯调参法使用不断更新的概率模型,通过推断过去的结果来'集中'有希望的超参数
贝叶斯优化问题的四个部分
1.目标函数 - 机器学习模型使用该组超参数在验证集上的损失
它的输入为一组超参数,输出需要最小化的值(交叉验证损失)
2.域空间 - 要搜索的超参数的取值范围
在搜索的每次迭代中,贝叶斯优化算法将从域空间为每个超参数选择一个值
当我们进行随机或网格搜索时,域空间是一个网格
而在贝叶斯优化中,不是按照顺序()网格)或者随机选择一个超参数,而是按照每个超参数的概率分布选择
3.优化算法 - 构造替代函数并选择下一个超参数值进行评估的方法
4.来自目标函数评估的存储结果,包括超参数和验证集上的损失
'''
from bayes_opt import BayesianOptimization
# 定义目标函数,我们要这个目标函数输出的值最小
def rf_cv(num_leaves, max_depth, subsample, min_child_samples):
val = cross_val_score(
LGBMRegressor(
objective='regression_l1', num_leaves=int(num_leaves), max_depth=int(max_depth),
subsample=subsample, min_child_samples=int(min_child_samples)),
X=train_X, y=train_y_In, verbose=0, cv=5, scoring=make_scorer(mean_absolute_error)
).mean()
return 1 - val
# 定义优化参数,即域空间
rf_bo = BayesianOptimization(rf_cv, {'num_leaves': (2, 100),
'max_depth': (2, 100), 'subsample': (0.1, 1),
'min_child_samples': (2, 100)}
)
# 开始优化
'''
rf_bo.maximize() - 最大化分数 这里的目标函数是1-MAE,应该是越大越好,所以用最大化分数
rf_bo.minimize() - 最小化分数
'''
rf_bo.maximize()
# 最优目标函数对应的MAE值
1 - rf_bo.max['target']
Target值一旦出现新高,就会标记紫色
观察最高的值为0.8694
MAE值为0.1306;
目前是三种调参方法中得到最高精度的一种
不难发现,随着对参数的调整,模型的精度在一点点提高
后续Task5 模型融合,最后的时刻到了~
作者:恶魔眼睛大又大���