Task4 建模调参
线性回归对于特征的要求;
处理长尾分布;
理解线性回归模型;
模型性能验证:评价函数与目标函数;
交叉验证方法;
留一验证方法;
针对时间序列问题的验证;
绘制学习率曲线;
绘制验证曲线;
嵌入式特征选择:Lasso回归;
Ridge回归;
决策树;
模型对比:常用线性模型;
常用非线性模型;
模型调参:贪心调参方法;
网格调参方法;
贝叶斯调参方法;
相关原理介绍与推荐线性回归模型:https://zhuanlan.zhihu.com/p/49480391
决策树模型:https://zhuanlan.zhihu.com/p/65304798
GBOT模型:https://zhuanlan.zhihu.com/p/45145899
XGBoost:https://zhuanlan.zhihu.com/p/86816771
LightGBM:https://zhuanlan.zhihu.com/p/89360721
推荐教材
《机器学习》
《统计学习方法》
《Python大战机器学习》
《面向机器学习的特征工程》
《数据科学家访谈录》
import pandas as pd
import numpy as np
import warnings
warnings.filterwarnings('ignore')
def reduce_mem_usage(df):
""" iterate through all the columns of a dataframe and modify the data type
to reduce memory usage.
"""
start_mem = df.memory_usage().sum()/ 1024**2
print('Memory usage of dataframe is {:.2f} MB'.format(start_mem))
for col in df.columns:
col_type = df[col].dtype
if col_type != object:
c_min = df[col].min()
c_max = df[col].max()
if str(col_type)[:3] == 'int':
if c_min > np.iinfo(np.int8).min and c_max np.iinfo(np.int16).min and c_max np.iinfo(np.int32).min and c_max np.iinfo(np.int64).min and c_max np.finfo(np.float16).min and c_max np.finfo(np.float32).min and c_max < np.finfo(np.float32).max:
df[col] = df[col].astype(np.float32)
else:
df[col] = df[col].astype(np.float64)
else:
df[col] = df[col].astype('category')
end_mem = df.memory_usage().sum()/ 1024**2
print('Memory usage after optimization is: {:.2f} MB'.format(end_mem))
print('Decreased by {:.1f}%'.format(100 * (start_mem - end_mem) / start_mem))
return df
# 参考:https://blog.csdn.net/wj1066/article/details/81124959,关于文章里面的代码,贴到下一个cell里了,进行了适当修改。
'''# @from: https://www.kaggle.com/arjanso/reducing-dataframe-memory-size-by-65/code
# @liscense: Apache 2.0
# @author: weijian
def reduce_mem_usage(props):
# 计算当前内存
start_mem_usg = props.memory_usage().sum() / 1024 ** 2
print("Memory usage of the dataframe is :", start_mem_usg, "MB")
# 哪些列包含空值,空值用-999填充。why:因为np.nan当做float处理
NAlist = []
for col in props.columns:
# 这里只过滤了object的格式,如果你的代码中还包含其他类型,请一并过滤
if (props[col].dtypes != object):
print("**************************")
print("columns: ", col)
print("dtype before", props[col].dtype)
# 判断是否是int类型
isInt = False
mmax = props[col].max()
mmin = props[col].min()
# Integer does not support NA, therefore Na needs to be filled
if not np.isfinite(props[col]).all(): #np.isfinite()判断数据是否为无穷大True where x is not positive infinity, negative infinity, or NaN; false otherwise.
NAlist.append(col)
props[col].fillna(-999, inplace=True) # 用-999填充
# test if column can be converted to an integer
asint = props[col].fillna(0).astype(np.int64)
result = np.fabs(props[col] - asint)
result = result.sum()
if result = 0: # 最小值大于0,转换成无符号整型
if mmax <= 255:
props[col] = props[col].astype(np.uint8)
elif mmax <= 65535:
props[col] = props[col].astype(np.uint16)
elif mmax np.iinfo(np.int8).min and mmax np.iinfo(np.int16).min and mmax np.iinfo(np.int32).min and mmax np.iinfo(np.int64).min and mmax np.finfo(np.float16).min and mmax np.finfo(np.float32).min and mmax < np.finfo(np.float32).max:
props[col] = props[col].astype(np.float32)
else:
props[col] = props[col].astype(np.float64)
props[col] = props[col].astype(np.float16)
print(col,"dtype after", props[col].dtype)
print("********************************")
else:
props[col] = props[col].astype('category')
print("___MEMORY USAGE AFTER COMPLETION:___")
mem_usg = props.memory_usage().sum() / 1024**2
print("Memory usage is: ",mem_usg," MB")
print("This is ",100*mem_usg/start_mem_usg,"% of the initial size")
return props, NAlist'''
sample_feature = reduce_mem_usage(pd.read_csv('C:\\Users\\lzf33\\Desktop\\used_car_train_20200313.csv',sep = ' '))
'''这里一开始有个bug困扰我很久,reduce_mem_usage之后,让我的内存占用扩大了5倍以上。
仔细查看原因,是因为我在读取数据的时候忘记加 sep = ' ',导致只出现一个特征,这个特征从object转换成了categary。
修改后内存降低3/4左右'''
Memory usage of dataframe is 35.48 MB
Memory usage after optimization is: 9.73 MB
Decreased by 72.6%
continuous_feature_names = [x for x in sample_feature.columns if x not in ['price','brand','model']]
线性回归 & 五折交叉验证 & 模拟真实业务情况
sample_feature = sample_feature.dropna().replace('-',0).reset_index(drop = True)#pd.dropna()删除缺失值(axis控制),pd.reset_index()还原索引,重新变为默认的整型索引
sample_feature['notRepairedDamage'] = sample_feature['notRepairedDamage'].astype(np.float32)
train = sample_feature[continuous_feature_names + ['price']]
train_X = train[continuous_feature_names]
train_Y = train['price']
简单建模
from sklearn.linear_model import LinearRegression
model = LinearRegression(normalize = True)
model = model.fit(train_X,train_Y)
查看线性回归模型的权重(coef)与截距(intercept)
print('intercept: ' + str(model.intercept_))
sorted(dict(zip(continuous_feature_names,model.coef_)).items(),key = lambda x:x[1],reverse = True)#key = lambda x:x[1]的意思是按照每一个字典的第1位作为排序的key
intercept: -4640457.8662025
[('v_6', 3673002.1419384754),
('v_8', 759591.7003447326),
('v_9', 471323.04315035365),
('v_12', 132283.3762441523),
('v_3', 84235.65527098377),
('v_11', 53411.28459388038),
('v_7', 52524.31643972741),
('v_10', 43276.59046978545),
('v_13', 39330.188069404365),
('gearbox', 1571.86326282151),
('bodyType', 197.94756541252525),
('power', 2.042439055841961),
('creatDate', 0.23427471450608905),
('regionCode', 0.06705727763304824),
('offerType', -2.769753336906433e-06),
('name', -2.988075294348636e-05),
('SaleID', -9.324241864682941e-05),
('regDate', -0.005483166270673471),
('notRepairedDamage', -125.41622147350512),
('fuelType', -159.34848893069645),
('seller', -269.96439790891003),
('kilometer', -306.3068222920057),
('v_14', -1593.0508199084825),
('v_0', -4475.057851914484),
('v_1', -17791.38956169945),
('v_5', -31715.93300766927),
('v_4', -44649.742287385285),
('v_2', -131259.7933339922)]
from matplotlib import pyplot as plt
subsample_index = np.random.randint(low = 0,high = len(train_Y),size = 50)
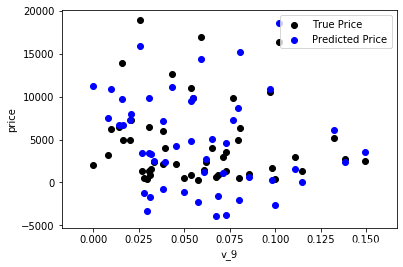
绘制特征v_9的值与标签的散点图,图片发现模型的预测结果(蓝色)与真实标签(黑色)的分布差异较大,且部分预测值出现了小于0的情况,说明我们的模型存在问题
plt.scatter(train_X['v_9'][subsample_index],train_Y[subsample_index],color = 'black')
plt.scatter(train_X['v_9'][subsample_index],model.predict(train_X.loc[subsample_index]),color = 'blue')
plt.xlabel('v_9')
plt.ylabel('price')
plt.legend(['True Price','Predicted Price'],loc = 'upper right')
print('The predicted price is obvious different from true price')
plt.show()
The predicted price is obvious different from true price
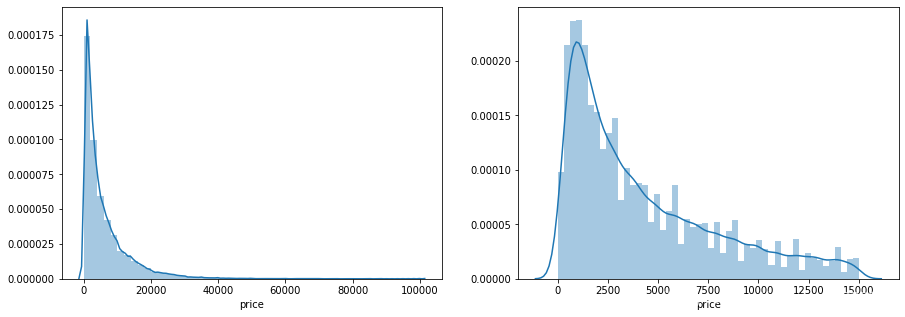
通过作图我们发现数据的标签(price)呈现长尾分布,不利于我们建模预测。原因是很多模型都假设数据误差项符合正态分布,而长尾分布的数据违背了这一假设。
参考博客:https://blog.csdn.net/Noob_daniel/article/details/76087829
import seaborn as sns
print('It is clear to see the price shows a typical exponential distribution')
plt.figure(figsize = (15,5))
plt.subplot(1,2,1) #plt.subplot()创建小图,见博客https://blog.csdn.net/TeFuirnever/article/details/89842795
sns.distplot(train_Y)
plt.subplot(1,2,2)
sns.distplot(train_Y[train_Y < np.quantile(train_Y,0.9)]) #进行长尾截断
It is clear to see the price shows a typical exponential distribution
对标签进行log(x+1)变换,使标签贴近正态分布
train_Y_ln = np.log(train_Y + 1)
import seaborn as sns
print('The transformed price seems like normal distribution')
plt.figure(figsize = (15,5))
plt.subplot(1,2,1)
sns.distplot(train_Y_ln)
plt.subplot(1,2,2)
sns.distplot(train_Y_ln[train_Y_ln < np.quantile(train_Y_ln,0.9)])
The transformed price seems like normal distribution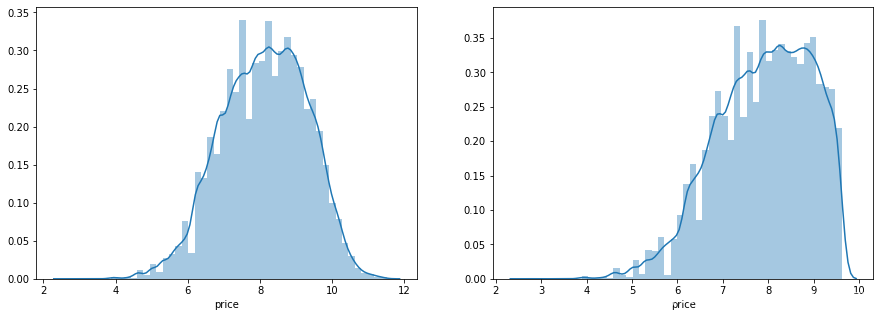
可以看出来,不截尾更加好一点
model = model.fit(train_X,train_Y_ln)
print('intercept: ' + str(model.intercept_))
sorted(dict(zip(continuous_feature_names,model.coef_)).items(),key = lambda x:x[1],reverse = True)
intercept: -353.3889681759144
[('v_5', 16.09065694926116),
('v_9', 11.972612801933929),
('v_7', 2.641441554685271),
('v_1', 2.0597877114904306),
('v_12', 1.424974732259648),
('v_13', 1.1948073544849587),
('v_3', 0.7763099340034495),
('v_11', 0.14195738474543731),
('gearbox', 0.04646668788565976),
('power', 8.233335079434495e-05),
('creatDate', 1.8709995340905467e-05),
('SaleID', 4.6557667722489505e-09),
('offerType', -9.021050573210232e-11),
('name', -6.10436692843396e-08),
('regDate', -2.51614293740505e-07),
('regionCode', -1.0033569518176233e-06),
('bodyType', -0.0006192852761664921),
('fuelType', -0.004586532008360247),
('kilometer', -0.008325123062295435),
('v_14', -0.02487755439125371),
('v_0', -0.10964201577676595),
('seller', -0.11027663559423836),
('notRepairedDamage', -0.24085825476106112),
('v_2', -0.31056631330649004),
('v_10', -0.7417529879268147),
('v_4', -1.1094649651533428),
('v_8', -34.75661341543952),
('v_6', -194.49188949904917)]
再次进行可视化,发现结果比较接近,并且未出现异常
plt.scatter(train_X['v_9'][subsample_index],train_Y[subsample_index],color = 'black')
plt.scatter(train_X['v_9'][subsample_index],np.exp(model.predict(train_X.loc[subsample_index]))-1,color = 'blue')
plt.xlabel('v_9')
plt.ylabel('price')
plt.legend(['True Price','Predicted Price'],loc = 'upper right')
print('The predicted price seems normal after np.log transforming')
plt.show()
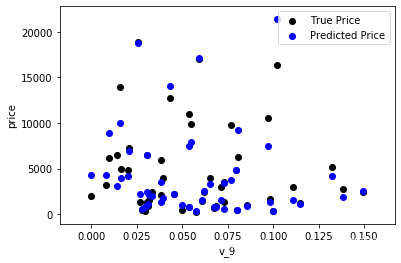
在使用训练集对参数进行训练的时候,经常会发现人们通常会将一整个训练集分为三个部分(比如mnist手写训练集)。一般分为:训练集(train_set),评估集(valid_set),测试集(test_set)这三个部分。这其实是为了保证训练效果而特意设置的。其中测试集很好理解,其实就是完全不参与训练的数据,仅仅用来观测测试效果的数据。而训练集和评估集则牵涉到下面的知识了。
因为在实际的训练中,训练的结果对于训练集的拟合程度通常还是挺好的(初始条件敏感),但是对于训练集之外的数据的拟合程度通常就不那么令人满意了。因此我们通常并不会把所有的数据集都拿来训练,而是分出一部分来(这一部分不参加训练)对训练集生成的参数进行测试,相对客观的判断这些参数对训练集之外的数据的符合程度。这种思想就称为交叉验证(Cross Validation)
from sklearn.model_selection import cross_val_score
from sklearn.metrics import mean_absolute_error , make_scorer
def log_transfer(func):
def wrapper(y,yhat):
result = func(np.log(y),np.nan_to_num(np.log(yhat)))
return result
return wrapper
scores = cross_val_score(model,X = train_X, y = train_Y,verbose = 1,cv = 5,scoring = make_scorer(log_transfer(mean_absolute_error)))
使用线性回归模型,对未处理标签的特征数据进行五折交叉验证
print('AVG:',np.mean(scores))
AVG: 1.4858341501285606
对于线性回归模型,对处理过标签的特征数据进行五折交叉验证
scores = cross_val_score(model,X = train_X, y = train_Y_ln,verbose = 1,cv = 5,scoring = make_scorer(mean_absolute_error))
print('AVG:',np.mean(scores))
AVG: 0.19396812188307244
scores = pd.DataFrame(scores.reshape(1,-1))
scores.columns = ['cv' + str(x) for x in range(1,6)]
scores.index = ['MAE']
scores
| cv1 | cv2 | cv3 | cv4 | cv5 | |
|---|---|---|---|---|---|
| MAE | 0.192335 | 0.194422 | 0.195198 | 0.192439 | 0.195447 |
但在事实上,由于我们并不具有预知未来的能力,五折交叉验证在某些与时间相关的数据集上反而反映了不真实的情况。通过2018年的二手车价格预测2017年的二手车价格,这显然是不合理的,因此我们还可以采用时间顺序对数据集进行分隔。在本例中,我们选用靠前时间的4/5样本当作训练集,靠后时间的1/5当作验证集,最终结果与五折交叉验证差距不大
import datetime
sample_feature = sample_feature.reset_index(drop = True)
split_point = len(sample_feature)//5*4 #" / "就表示 浮点数除法,返回浮点结果;" // "表示整数除法
train = sample_feature.loc[:split_point].dropna()
val = sample_feature.loc[split_point:].dropna()
train_X = train[continuous_feature_names]
train_Y_ln = np.log(train['price'] + 1)
val_X = val[continuous_feature_names]
val_Y_ln = np.log(val['price'] + 1)
model = model.fit(train_X, train_Y_ln)
mean_absolute_error(val_Y_ln, model.predict(val_X))
0.19542563472952243
绘制学习率曲线与验证曲线
from sklearn.model_selection import learning_curve,validation_curve
?learning_curve
?validation_curve
def plot_learning_curve(estimator,title,X,y,ylim = None,cv = None,n_jobs = 1,train_sizes = np.linspace(0.1,1.0,5)):
plt.figure()
plt.title(title)
if ylim is not None:
plt.ylim(*ylim)
plt.xlabel('Training example')
plt.ylabel('score')
train_sizes,train_scores,test_scores = learning_curve(estimator,X,y,cv = cv,n_jobs = n_jobs,train_sizes = train_sizes,scoring = make_scorer(mean_absolute_error))
train_score_mean = np.mean(train_scores,axis = 1)
train_score_std = np.std(train_scores,axis = 1)
test_score_mean = np.mean(test_scores,axis = 1)
test_score_std = np.std(test_scores,axis = 1)
plt.grid()#趋于
plt.fill_between(train_sizes,train_score_mean - train_score_std,
train_score_mean + train_score_std,alpha = 0.1,
color = 'r')
plt.fill_between(train_sizes,test_score_mean - test_score_std,
test_score_mean + test_score_std,alpha = 0.1,
color = 'g')
plt.plot(train_sizes,train_score_mean,'o-',color = 'r',label = 'Training score')
plt.plot(train_sizes,test_score_mean,'o-',color = 'g',label = 'Cross-validation score')
plt.legend(loc = 'best')
return plt
plot_learning_curve(LinearRegression(),'Liner_model',train_X[:1000],train_Y_ln[:1000],
ylim = (0,.5),cv = 5,n_jobs =1)
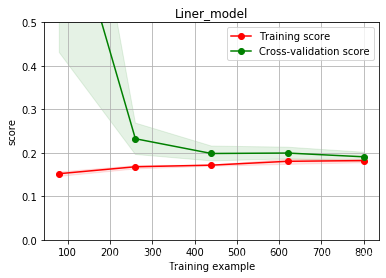
train = sample_feature[continuous_feature_names + ['price']].dropna()
train_X =train[continuous_feature_names]
train_y = train['price']
train_y_ln = np.log(train_y + 1)
线性模型&嵌入式特征选择
用简单易懂的语言描述「过拟合 overfitting」:https://www.zhihu.com/question/32246256/answer/55320482
模型复杂度与模型的泛化能力 :http://yangyingming.com/article/434/
正则化的直观理解 :https://blog.csdn.net/jinping_shi/article/details/52433975
在过滤式和包裹式特征选择方法中,特征选择过程与学习器训练过程有明显的分别。而嵌入式特征选择在学习器训练过程中自动地进行特征选择。嵌入式选择最常用的是L1正则化与L2正则化。在对线性回归模型加入两种正则化方法后,他们分别变成了岭回归与Lasso回归。
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Ridge
from sklearn.linear_model import Lasso
models = [LinearRegression(),
Ridge(),
Lasso()]
result = dict()
for model in models:
model_name = str(model).split('(')[0]
scores = cross_val_score(model,X = train_X,y = train_y_ln,verbose = 0,cv = 5,
scoring = make_scorer(mean_absolute_error))
result[model_name] = scores
print(model_name + ' is finished')
LinearRegressionis finished
Ridgeis finished
Lassois finished
result = pd.DataFrame(result)
result.index = ['cv' + str(x) for x in range(1,6)]
result
| LinearRegression | Ridge | Lasso | |
|---|---|---|---|
| cv1 | 0.192335 | 0.195663 | 0.553412 |
| cv2 | 0.194422 | 0.198016 | 0.553226 |
| cv3 | 0.195198 | 0.198385 | 0.558305 |
| cv4 | 0.192439 | 0.195997 | 0.544775 |
| cv5 | 0.195447 | 0.198846 | 0.552216 |
model = LinearRegression().fit(train_X,train_y_ln)
print('intercept:' + str(model.intercept_))
sns.barplot(abs(model.coef_),continuous_feature_names)
intercept:-353.3889681757323
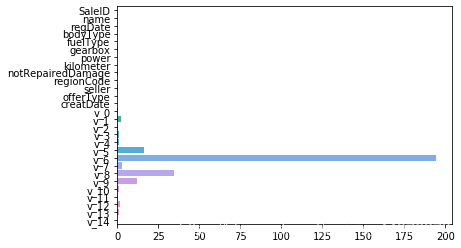
L2正则化在拟合过程中通常都倾向于让权值尽可能小,最后构造一个所有参数都比较小的模型。因为一般认为参数值小的模型比较简单,能适应不同的数据集,也在一定程度上避免了过拟合现象。可以设想一下对于一个线性回归方程,若参数很大,那么只要数据偏移一点点,就会对结果造成很大的影响;但如果参数足够小,数据偏移得多一点也不会对结果造成什么影响,专业一点的说法是『抗扰动能力强』
model = Ridge().fit(train_X,train_y_ln)
print('intercept:' + str(model.intercept_))
sns.barplot(abs(model.coef_),continuous_feature_names)
intercept:-336.66002067557463
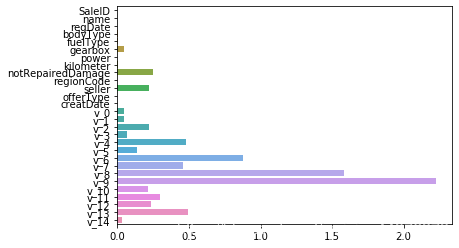
L1正则化有助于生成一个稀疏权值矩阵,进而可以用于特征选择。如下图,我们发现power与reg_Date特征非常重要。
model = Lasso().fit(train_X,train_y_ln)
print('intercept:' + str(model.intercept_))
sns.barplot(abs(model.coef_),continuous_feature_names)
intercept:-318.583884324992
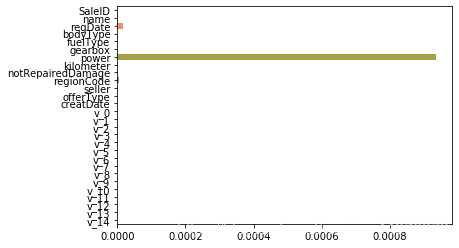
除此之外,决策树通过信息熵或GINI指数选择分裂节点时,优先选择的分裂特征也更加重要,这同样是一种特征选择的方法。XGBoost与LightGBM模型中的model_importance指标正是基于此计算的
非线性模型from sklearn.linear_model import LinearRegression
from sklearn.svm import SVC
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.neural_network import MLPRegressor
from xgboost.sklearn import XGBRegressor
from lightgbm.sklearn import LGBMRegressor
models = [LinearRegression(),
DecisionTreeRegressor(),
RandomForestRegressor(),
GradientBoostingRegressor(),
MLPRegressor(solver = 'lbfgs',max_iter = 100),
XGBRegressor(n_estimators = 100,objective = 'reg:squarederror'),
LGBMRegressor(n_estimators = 100)]
result = dict()
for model in models:
model_name = str(model).split('(')[0]
scores = cross_val_score(model,X = train_X,y = train_y_ln,verbose = 0,cv = 5,
scoring = make_scorer(mean_absolute_error))
result[model_name] = scores
print(model_name + ' is finished')
LinearRegression is finished
DecisionTreeRegressor is finished
RandomForestRegressor is finished
GradientBoostingRegressor is finished
MLPRegressor is finished
XGBRegressor is finished
LGBMRegressor is finished
result = pd.DataFrame(result)
result.index = ['cv' + str(x) for x in range(1, 6)]
result
| LinearRegression | DecisionTreeRegressor | RandomForestRegressor | GradientBoostingRegressor | MLPRegressor | XGBRegressor | LGBMRegressor | |
|---|---|---|---|---|---|---|---|
| cv1 | 0.192335 | 0.193119 | 0.139150 | 0.169962 | 84.315911 | 0.136735 | 0.140480 |
| cv2 | 0.194422 | 0.187340 | 0.137284 | 0.171832 | 2.025594 | 0.135895 | 0.142535 |
| cv3 | 0.195198 | 0.186012 | 0.138100 | 0.170776 | 13.669518 | 0.138404 | 0.142944 |
| cv4 | 0.192439 | 0.186382 | 0.137157 | 0.170079 | 152.840603 | 0.135897 | 0.140436 |
| cv5 | 0.195447 | 0.190387 | 0.140328 | 0.171890 | 62.698873 | 0.151519 | 0.141795 |
可以看到XGB和RF效果比较好
模型调参几种常见的调参方法:
贪心算法 https://www.jianshu.com/p/ab89df9759c8
网格调参 https://blog.csdn.net/weixin_43172660/article/details/83032029
贝叶斯调参 https://blog.csdn.net/linxid/article/details/81189154
## LGB的参数集合
objective = ['regression','regression_l1','mape','huber','fair']
num_leaves = [3,5,10,15,20,40,55]
max_depth = [3,5,10,15,20,40,55]
bagging_fraction = []
feature_fraction = []
drop_rate = []
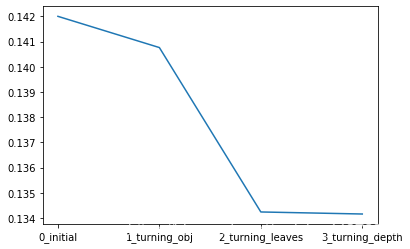
贪心调参
best_obj = dict()
for obj in objective:
model = LGBMRegressor(objective=obj)
score = np.mean(cross_val_score(model, X=train_X, y=train_y_ln, verbose=0, cv = 5, scoring=make_scorer(mean_absolute_error)))
best_obj[obj] = score
best_leaves = dict()
for leaves in num_leaves:
model = LGBMRegressor(objective=min(best_obj.items(), key=lambda x:x[1])[0], num_leaves=leaves)
score = np.mean(cross_val_score(model, X=train_X, y=train_y_ln, verbose=0, cv = 5, scoring=make_scorer(mean_absolute_error)))
best_leaves[leaves] = score
best_depth = dict()
for depth in max_depth:
model = LGBMRegressor(objective=min(best_obj.items(), key=lambda x:x[1])[0],
num_leaves=min(best_leaves.items(), key=lambda x:x[1])[0],
max_depth=depth)
score = np.mean(cross_val_score(model, X=train_X, y=train_y_ln, verbose=0, cv = 5, scoring=make_scorer(mean_absolute_error)))
best_depth[depth] = score
sns.lineplot(x=['0_initial','1_turning_obj','2_turning_leaves','3_turning_depth'], y=[0.142 ,min(best_obj.values()), min(best_leaves.values()), min(best_depth.values())])
from sklearn.model_selection import GridSearchCV
import time
start = time.time()
parameters = {'objective': objective , 'num_leaves': num_leaves, 'max_depth': max_depth}
model = LGBMRegressor()
clf = GridSearchCV(model, parameters, cv=5)
clf = clf.fit(train_X, train_y)
end = time.time()
Time usage: 3435.413674354553
print('Time cost: %.2f mins'%((end-start)/60))
Time cost: 57.26 mins
太糟心了。
clf.best_params_
{'max_depth': 15, 'num_leaves': 55, 'objective': 'regression'}
model = LGBMRegressor(objective='regression',
num_leaves=55,
max_depth=15)
np.mean(cross_val_score(model, X=train_X, y=train_y_ln, verbose=0, cv = 5, scoring=make_scorer(mean_absolute_error)))
0.13576304815119178
贝叶斯调参
from bayes_opt import BayesianOptimization
#pip install bayesian-optimization -i https://pypi.tuna.tsinghua.edu.cn/simple
def rf_cv(num_leaves, max_depth, subsample, min_child_samples):
val = cross_val_score(
LGBMRegressor(objective = 'regression_l1',
num_leaves=int(num_leaves),
max_depth=int(max_depth),
subsample = subsample,
min_child_samples = int(min_child_samples)
),
X=train_X, y=train_y_ln, verbose=0, cv = 5, scoring=make_scorer(mean_absolute_error)
).mean()
return 1 - val
rf_bo = BayesianOptimization(
rf_cv,
{
'num_leaves': (2, 100),
'max_depth': (2, 100),
'subsample': (0.1, 1),
'min_child_samples' : (2, 100)
}
)
rf_bo.maximize()
| iter | target | max_depth | min_ch... | num_le... | subsample |
-------------------------------------------------------------------------
| 1 | 0.8379 | 79.83 | 95.23 | 9.55 | 0.5292 |
| 2 | 0.8546 | 19.79 | 8.661 | 22.77 | 0.6102 |
| 3 | 0.864 | 81.51 | 76.67 | 48.5 | 0.8308 |
| 4 | 0.8696 | 42.2 | 16.94 | 87.93 | 0.4881 |
| 5 | 0.869 | 24.17 | 8.017 | 82.43 | 0.7794 |
| 6 | 0.8266 | 3.341 | 99.44 | 97.89 | 0.716 |
| 7 | 0.8029 | 99.67 | 4.454 | 3.821 | 0.6179 |
| 8 | 0.8703 | 94.95 | 96.83 | 96.82 | 0.6135 |
| 9 | 0.8705 | 99.82 | 4.743 | 99.8 | 0.6146 |
| 10 | 0.8704 | 96.98 | 2.802 | 98.32 | 0.9267 |
| 11 | 0.8704 | 99.89 | 59.01 | 98.84 | 0.3906 |
| 12 | 0.8672 | 99.33 | 95.96 | 70.99 | 0.2127 |
| 13 | 0.8702 | 69.25 | 4.373 | 97.82 | 0.8791 |
| 14 | 0.8669 | 43.92 | 3.382 | 66.72 | 0.1602 |
| 15 | 0.8683 | 54.06 | 58.56 | 75.98 | 0.9883 |
| 16 | 0.8696 | 99.55 | 54.67 | 90.58 | 0.9481 |
| 17 | 0.8069 | 2.329 | 2.687 | 95.96 | 0.3651 |
| 18 | 0.8132 | 3.359 | 98.5 | 4.709 | 0.9548 |
| 19 | 0.8069 | 2.589 | 43.86 | 45.98 | 0.9593 |
| 20 | 0.866 | 46.89 | 99.81 | 58.92 | 0.8977 |
| 21 | 0.7715 | 6.452 | 2.515 | 2.8 | 0.9661 |
| 22 | 0.8132 | 48.36 | 41.77 | 4.929 | 0.9333 |
| 23 | 0.87 | 60.7 | 99.23 | 96.9 | 0.9759 |
| 24 | 0.8702 | 62.7 | 51.22 | 99.65 | 0.9881 |
| 25 | 0.8645 | 18.37 | 2.671 | 50.26 | 0.876 |
| 26 | 0.8587 | 47.51 | 2.067 | 30.65 | 0.5223 |
| 27 | 0.8616 | 99.71 | 52.49 | 38.54 | 0.8097 |
| 28 | 0.8599 | 99.68 | 97.36 | 33.95 | 0.8419 |
| 29 | 0.87 | 43.25 | 2.006 | 96.91 | 0.8451 |
| 30 | 0.8633 | 38.29 | 25.26 | 45.69 | 0.9467 |
=========================================================================
1 - rf_bo.max['target']
0.12951832033940058
总结
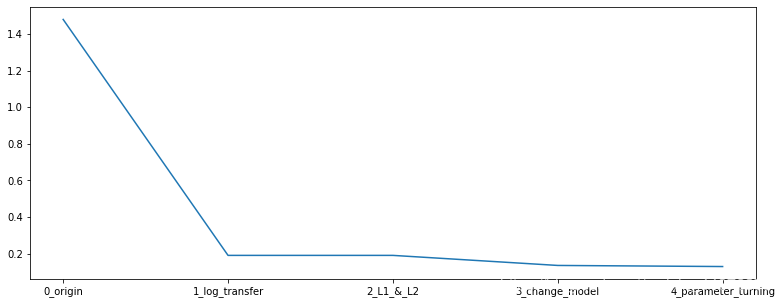
在本章中,我们完成了建模与调参的工作,并对我们的模型进行了验证。此外,我们还采用了一些基本方法来提高预测的精度,提升如下图所示。
plt.figure(figsize=(13,5))
sns.lineplot(x=['0_origin','1_log_transfer','2_L1_&_L2','3_change_model','4_parameter_turning'], y=[1.48 ,0.19, 0.19, 0.135, 0.129])
作者:weixin_44976373