【sklearn非线性回归预测】交叉验证评估与调参
交叉验证调参与交叉验证评估的区别与使用
什么是交叉验证
作者：HUST_YZY
交叉验证原理
交叉验证原理与常用方法
scikitlearn交叉验证评估
交叉验证：评估估算器的表现
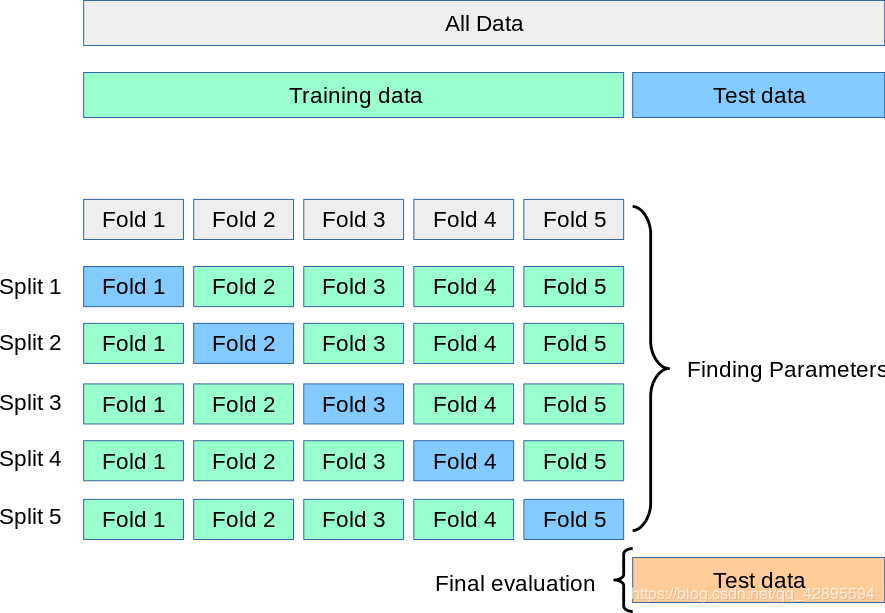在交叉验证中数据集一般可以分为训练集和测试集，其中训练集的某一折用于作为验证集，这样有利于充分利用数据，但是同样提升了计算量。交叉验证的使用往往时代码运行缓慢。
交叉验证一方面可以用于调整超参数，也即是通过反复的交叉训练，找到模型最优的超参数，比如使用网格搜索GridSearchCV()。另一方面用于评估模型在数据集上的表现，比如cross_val_score()。
交叉验证评估： 针对在训练集上训练得到的模型表现良好，但在测试集的预测结果不理想，即模型出现过拟合(overfitting)，偏差(bias)低而方差(variance)高，泛化能力差的情况。也就是说交叉验证用于评估模型的预测性能。此外，也可以用于从有限数据中获取尽可能多的有效信息。
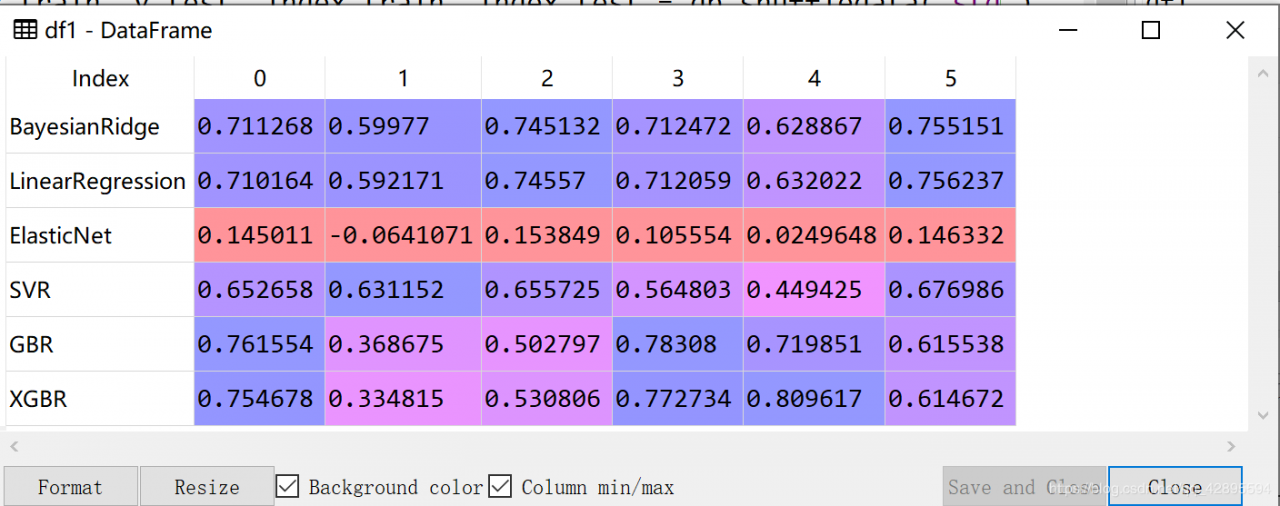
实际使用方法 交叉验证评估在针对回归问题上，我们首先需要确定选用的模型，如何确定哪个模型更好？，便可以采用交叉验证评估的方法选取评分较高且稳定的模型。如下图所示，针对不同的模型采用6折交叉验证评分。针对每个模型的每次训练给出了一个评分，6折也就是每个模型6个评分。
可见BayesianRidge，GBR， XGBR模型的评分较高且比较稳定，因此可以选用这三个模型以进行更进一步的选择。
# -*- coding: utf-8 -*-
"""
Created on Wed Mar 4 10:49:07 2020
@author: 85845
"""
import numpy as np
import dataprocess as dp # 自己写的数据预处理的模块
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import
BayesianRidge, LinearRegression, ElasticNet
from sklearn.svm import SVR
from sklearn.ensemble.gradient_boosting
import GradientBoostingRegressor
import xgboost as xgb
from sklearn.model_selection import
cross_val_score
from sklearn.metrics import
explained_variance_score, mean_absolute_error, mean_squared_error, r2_score
# 评估指标介绍https://www.cnblogs.com/mdevelopment/p/9456486.html
# EV: 解释回归模型的方差得分，[0,1]，接近1说明自变量越能解释因变量的方差变化
# MAE: 平均绝对误差，评估预测结果和真实数据集的接近程度的程度，越小越好
# MSE: 均方差，
计算拟合数据和原始数据对应样本点的误差的平方和的均值，越小越好
# R2: 判定系数，解释回归模型的方差得分，[0,1]，接近1说明自变量越能解释因变量的方差变化。
#
=============================================================================
# 导入最大最小归一化后的数据
X_train, X_test, y_train, y_test, index_train,
index_test = dp.shuffledata('std')
n_folds = 6 # 设置交叉检验的次数
model_br = BayesianRidge() # 建立贝叶斯回归模型
model_lr = LinearRegression() # 建立普通线性回归模型
model_etc = ElasticNet() # 建立弹性网络回归模型
model_svr = SVR() # 建立支持向量回归模型
model_gbr = GradientBoostingRegressor() # 建立梯度增强回归模型
model_xgb = xgb.XGBRegressor(objective =
'reg:squarederror') # XGBoost回归模型
model_names = ['BayesianRidge',
'LinearRegression',
'ElasticNet', 'SVR', 'GBR',
'XGBR']
model_dir = [model_br, model_lr, model_etc,
model_svr, model_gbr, model_xgb]
#
=============================================================================
# 交叉验证评分与模型训练
cv_score_list = [] # 交叉检验结果列表
y_train_pre = [] # 各个模型预测的y值列表
y_test_pre = [] # 创建测试集预测结果列表
for model in model_dir:
scores = cross_val_score(model, X_train, y_train,
cv = n_folds,
scoring = 'r2')
#
对每个回归模型进行交叉验证
cv_score_list.append(scores) # 将验证结果保存在列表中
y_train_pre.append(model.fit(X_train, y_train).predict(X_train))
y_test_pre.append(model.fit(X_train, y_train).predict(X_test))
#
将训练模型的预测结果保存在列表中
#
=============================================================================
# 模型效果评估
n_samples, n_features = X_train.shape # 总训练样本量，总特征量
n_samples_test = X_test.shape[0]
model_metrics_name =
[explained_variance_score, mean_absolute_error,
mean_squared_error,
r2_score]
model_metrics_list = [] # 回归评价指标列表
在上述的三个模型中，需要对模型更进一步的调参，如何进行调参，则可以通过采用网格搜索的方法确定最优参数。如下例子，针对XBG模型的参数，首先可以通过字典给出调参的范围，[0.1,0.07]指的是两个可选值（注意不是范围）。因此网格搜索就相当于在parameters所给的参数中进行选择。然后可以给出最优模型的评分以及最优模型的参数。
model_xgb = xgb.XGBRegressor(objective ='reg:squarederror')
parameters = {'loss':['ls','lad','huber','quantile'],
'learning_rate':[0.1,0.07], #(0,1]之间的超参数
'n_estimators':[100,150],
'max_depth':[2,3,4], #设置树的深度
'min_samples_split': [2, 3, 4], #拆分内部节点所需的最少样本数
'min_samples_leaf':[1,2,3,4]} #在叶结点处所需的最小样本数
model_gs = GridSearchCV(model_gbr, parameters,cv=5)
model_gs.fit(X,y)
print('GBR Best score is:',model_gs.best_score_)
print('GBR Best parameter is:',model_gs.best_params_)
作者：HUST_YZY
