零基础数据挖掘入门系列(五) - 模型建立与调参
思维导图:零基础入门数据挖掘的学习路径
1. 写在前面零基础入门数据挖掘是记录自己在Datawhale举办的数据挖掘专题学习中的所学和所想, 该系列笔记使用理论结合实践的方式,整理数据挖掘相关知识,提升在实际场景中的数据分析、数据清洗,特征工程、建模调参和模型融合等技能。所以这个系列笔记共五篇重点内容, 也分别从上面五方面进行整理学习, 既是希望能对知识从实战的角度串联回忆,加强动手能力的锻炼,也希望这五篇笔记能够帮助到更多喜欢数据挖掘的小伙伴,我们一起学习,一起交流吧。
既然是理论结合实践的方式,那么我们是从天池的一个二手车交易价格预测比赛出发进行学习,既可以学习到知识,又可以学习如何入门一个数据竞赛, 下面我们开始吧。
今天是本系列的第五篇文章模型的建立与调参部分,这一块也是很费时间且核心的一部分工作,毕竟特征工程也好,数据清洗也罢,都是为最终的模型来服务的,模型的建立和调参才决定了最终的结果,上限是一回事, 如何更好的去达到这个上限又是一回事, 前一篇我们已经做完了特征工程,好像是有了一个上限,到底应该怎么去达到这个上限呢? 就需要看我们的模型表现了。所以今天重点整理模型的评估和调参的相关技术。
首先,我们会先从简单的线性模型开始,看看如何去建立一个模型以及建立完模型之后要去分析什么东西, 然后我们会学习交叉验证的思想和技术(这个在评估模型的效果是经常会用到)并且会构建一个线下测试集(当然这个针对本比赛), 上面的这些算是建立模型的基础,然后我们会尝试建立更多的模型去解决这个问题,并对比它们的效果, 当把模型选择出来之后,我们还得掌握一些调参的技术发挥模型最大的性能, 模型选择出来之后,也调完参数,但是模型真的就没有问题了吗? 我们其实不知道, 所以最后我们学习绘制学习率曲线看模型是否存在过拟合或者欠拟合的问题并给出相应的解决方法。
大纲如下:
我们先从最简单的模型开始(线性回归 & 交叉验证 & 构建线下测试集) 评估算法模型的框架(这里会给出一个选择模型的框架,适合迁移) 模型的调参技术(贪心调参, GridSearchCV调参和贝叶斯调参) 绘制学习曲线和验证曲线(如何从学习曲线看过拟合欠拟合以及如果发生了过拟合欠拟合问题,我们应该怎么去尝试解决) 对模型建立和调参部分的总结PS: 本文默认学习者已经具备了机器学习和数据挖掘的基础知识,已经知道了一些基本概念,比如过拟合,欠拟合,正则化,模型复杂度等。 所以关于这些基础知识,本文不会过多的赘述,遇到了会提一下,如果没有掌握这些基本概念,建议先去补一下这些基本的概念,可以参考后面的第一篇链接。并且关于模型的原理部分,这里也不展开论述, 因为关于这个比赛后面我尝试用了五六种模型进行试验,如果单纯讲这些模型的原理,篇幅会超级长,也不是这个系列需要整理的问题了, 这些东西我都放在了链接里面。
Ok, let’s go!
2. 我们先从简单的线性模型开始这部分也算是一个热身了,我们这个比赛是关于价格预测的,我们也知道了这是个回归的问题, 那么对于回归的问题,我们肯定是要选择一些回归模型来解决,线性模型就是一个比较简单的回归模型了, 所以我们就从这个模型开始,看看针对这个模型,我们会得到什么结果以及这些结果究竟是什么含义。
那么什么是线性回归模型, 线性回归(Linear Regression)是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析, 简单的说,假设我们预测的二手车价格我们用YYY来表示, 而我们构造的特征我们用xix_ixi, 我们就可以建立这样一个等式来表示它们的关系:
Y=w1x1+w2x2+....+wnxn+bY = w_1x_1+w_2x_2+....+w_nxn+bY=w1x1+w2x2+....+wnxn+b
训练模型的过程其实就是根据训练集的这些(X,Y)(X, Y)(X,Y)样本来求出合适的权重www, 然后对新的测试集XXX预测相应的YtestY_{test}Ytest, 这个YtestY_{test}Ytest其实就是我们想要的答案。这就是这部分的逻辑,下面看实现。
首先导入上次特征工程处理完毕后保存的数据集:
# 导入之前处理好的数据
data = pd.read_csv('./pre_data/pre_data.csv')
data.head()
# 然后训练集和测试集分开
train = data[:train_data.shape[0]]
test = data[train_data.shape[0]:] # 这个先不用
# 选择那些数值型的数据特征
continue_fea = ['power', 'kilometer', 'v_2', 'v_3', 'v_4', 'v_5', 'v_6', 'v_10', 'v_11', 'v_12', 'v_14',
'v_std', 'fuelType_price_average', 'gearbox_std', 'bodyType_price_average', 'brand_price_average',
'used_time', 'estivalue_price_average', 'estivalueprice_std', 'estivalue_price_min']
train_x = train[continue_fea]
train_y = train_data['price']
可以看一下,我这边处理的data数据的结果:

我这边data会有38个特征。
下面,我们建立线性模型,建立模型如果用sklearn的话还是非常简单的,包括训练和预测。
from sklearn.linear_model import LinearRegression
model = LinearRegression(normalize=True)
model.fit(train_x, train_y)
通过上面这两行代码,我们其实就建立了线性模型,并完成了训练。 .fit方法就是训练模型, 训练的结果就是求出了上面的w和b。我们可以查看一下:
"""查看训练的线性回归模型的截距(intercept)与权重(coef)"""
print('intercept: ' + str(model.intercept_))
sorted(dict(zip(continue_fea, model.coef_)).items(), key=lambda x: x[1], reverse=True)
## 结果:
intercept: -178881.74591832393
[('v_6', 482008.29891714785),
('v_std', 23713.66414841167),
('v_10', 7035.056136559963),
('v_14', 1418.4037751433352),
('used_time', 186.48306334062053),
('power', 12.19202369791551),
('estivalue_price_average', 0.4082359327905722),
('brand_price_average', 0.38196351334425965),
('gearbox_std', 0.1716754674248321),
('fuelType_price_average', 0.023785798378739224),
('estivalueprice_std', -0.016868767797045624),
('bodyType_price_average', -0.21364358471329278),
('kilometer', -155.11999534761347),
('estivalue_price_min', -574.6952072539285),
('v_11', -1164.0263997737668),
('v_12', -1953.0558048250668),
('v_4', -2198.03802357537),
('v_3', -3811.7514971187525),
('v_2', -5116.825271420712),
('v_5', -447495.6394686485)]
上面的这些就是我们那个等式中每个x前面的系数, intercept这个代表那个b, 我们上面说过了,有了系数,我们就可以对新的样本进行预测。 预测也很简单,只需要
y_pred = model.predict(x_test)
这样的一句代码就可以实现, 但是这里想探索一点别的东西, 因为后面模型对比中会发现线性模型的效果不好,因为我们前面特征选择的时候也看到过了啊, 并不是所有的数值特征都和price有相关关系啊, 还有一些非线性关系吧, 这些线性模型就捕捉不到了,并且一般线性模型喜欢那种归一化或者标准化的数据, 导致和非线性模型的数据还得分开处理,所以这个比赛不会用到线性模型。
但是关于线性模型还有些好玩的东西我们得了解一下, 比如从这些权重中如何看出哪个特征对线性模型来说更加重要些? 这个其实我们看的是权重的绝对值,因为正相关和负相关都是相关, 越大的说明那个特征对线性模型影响就越大。
其次,我们还可以看一下线性回归的训练效果,绘制一下v_6这个特征和标签的散点图:
subsample_index = np.random.randint(low=0, high=len(train_y), size=50)
plt.scatter(train_x['v_6'][subsample_index], train_y[subsample_index], color='black')
plt.scatter(train_x['v_6'][subsample_index], model.predict(train_x.loc[subsample_index]), color='blue')
plt.xlabel('v_6')
plt.ylabel('price')
plt.legend(['True Price','Predicted Price'],loc='upper right')
print('The predicted price is obvious different from true price')
plt.show()
结果如下:
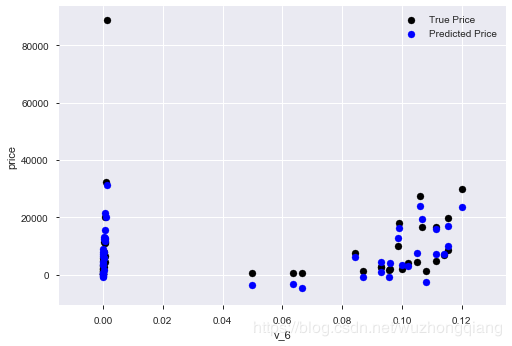
从上图中我们可以发现发现模型的预测结果(蓝色点)与真实标签(黑色点)的分布差异较大,且部分预测值出现了小于0的情况,说明我们的模型存在一些问题。 这个还是需要会看的,从这里我们也可以看出或许price这个需要处理一下。
哈哈,我们记得price的分布图吗?
print('It is clear to see the price shows a typical exponential distribution')
plt.figure(figsize=(15,5))
plt.subplot(1,2,1)
sns.distplot(train_y)
plt.subplot(1,2,2)
sns.distplot(train_y[train_y < np.quantile(train_y, 0.9)])
结果是长这个样子:
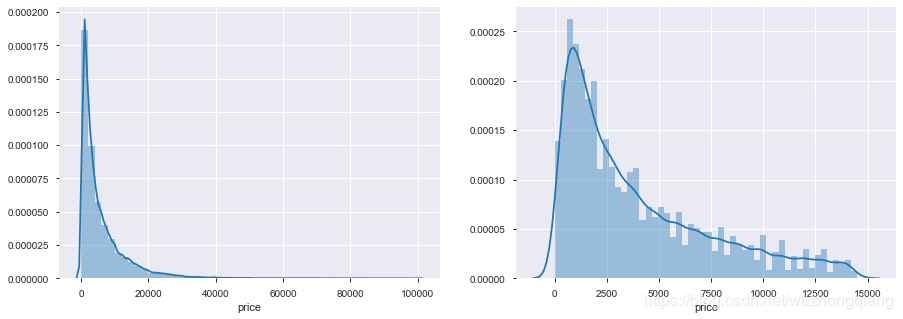
通过作图我们发现数据的标签(price)呈现长尾分布,不利于我们的建模预测。原因是很多模型都假设数据误差项符合正态分布,而长尾分布的数据违背了这一假设。参考博客:https://blog.csdn.net/Noob_daniel/article/details/76087829
所以,我们不妨取对数一下:
train_y_ln = np.log1p(train_y)
print('The transformed price seems like normal distribution')
plt.figure(figsize=(15,5))
plt.subplot(1,2,1)
sns.distplot(train_y_ln)
plt.subplot(1,2,2)
sns.distplot(train_y_ln[train_y_ln < np.quantile(train_y_ln, 0.9)])
这样效果是不是就好多了呢?
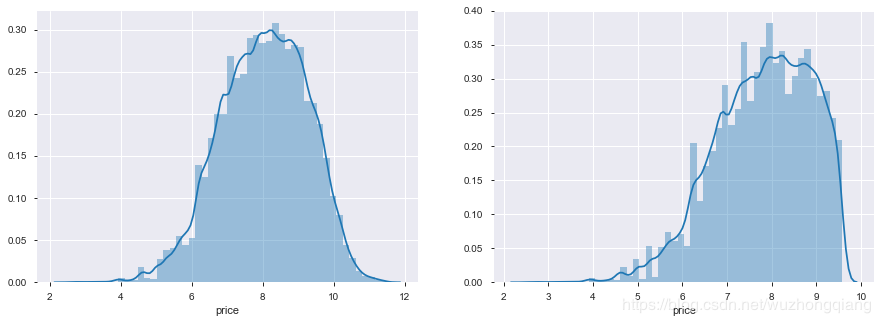
那么我们再来训练一下:
model = model.fit(train_x, train_y_ln)
print('intercept:'+ str(model.intercept_))
sorted(dict(zip(continue_fea, model.coef_)).items(), key=lambda x:x[1], reverse=True)
这个权重结果就不显示了,我们依然是画出v_6和price的散点图, 会发现长这样子了:
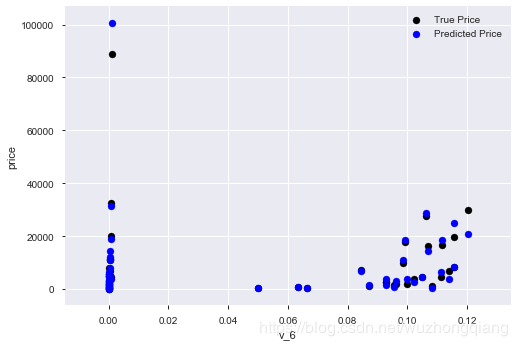
好了,线性回归模型我们就探索到这里,引入这块到底要表达个什么意思呢?
上面的三个点你get到了吗? 是不是这个热身中也潜藏好多知识