二手车交易价格预测_Task5_模型融合
模型融合_代码示例部分
#导入工具包
作者:恶魔眼睛大又大���
import numpy as np
import pandas as pd
from sklearn import metrics
from sklearn import linear_model
from sklearn.datasets import make_blobs # 这是打包好的波士顿房价数据集
from sklearn import datasets
from sklearn.tree import DecisionTreeClassifier # 分类决策树模型
from sklearn.ensemble import RandomForestClassifier # 随机森林回归模型
from sklearn.ensemble import VotingClassifier # 分类投票模型
from xgboost import XGBClassifier # xgboost用于解决f分类问题
from sklearn.linear_model import LogisticRegression # 逻辑回归模型
from sklearn.svm import SVC # 支持向量机模型 - 用于分类问题
from sklearn.svm import SVR # 支持向量机模型 - 用于回归问题
from sklearn.model_selection import train_test_split # 用于拆分训练集和测试集
from sklearn.datasets import make_moons # 创建月亮形的数据集
from sklearn.metrics import accuracy_score, roc_auc_score # ROC-Auc指标,评价模型得分用的
from sklearn.model_selection import cross_val_score # 用于做交叉验证
from sklearn.model_selection import GridSearchCV # 用于网格搜索
from sklearn.model_selection import StratifiedKFold # 分层交叉验证,每一折中都保持着原始数据中各个类别的比例关系
from sklearn.ensemble import ExtraTreesClassifier, GradientBoostingClassifier, GradientBoostingRegressor
import lightgbm as lgb
import xgboost as xgb
from sklearn.metrics import mean_squared_error, mean_absolute_error
import itertools # 用于创建自定义的迭代器
import seaborn as sns
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec # 用于调整子图的位置大小
from sklearn.neighbors import KNeighborsClassifier # k近邻分类算法
from sklearn.naive_bayes import GaussianNB # 先验为高斯分布的朴素贝叶斯
from mlxtend.classifier import StackingClassifier # 快速完成对sklearn模型的stacking
from mlxtend.plotting import plot_learning_curves # 绘制学习曲线
from mlxtend.plotting import plot_decision_regions # 绘制决策边界
from sklearn import preprocessing # 数据归一化(标准化)
from sklearn.decomposition import PCA, FastICA, FactorAnalysis, SparsePCA # 用于降维等特征处理
import warnings
warnings.filterwarnings('ignore') # 忽略警告
# 简单加权平均-结果直接融合
'''
生成一些简单的样本数据,
test_prei - 代表第i个模型的预测值
y_test_true - 代表真实值
'''
test_pre1 = [1.2, 3.2, 2.1, 6.2]
test_pre2 = [0.9, 3.1, 2.0, 5.9]
test_pre3 = [1.1, 2.9, 2.2, 6.0]
y_test_true = [1, 3, 2, 6]
# 定义结果的加权平均函数 - 根据加权计算
def weighted_method(test_pre1, test_pre2, test_pre3, w=[1/3, 1/3, 1/3]):
weighted_result = w[0] * pd.Series(test_pre1) + w[1] * pd.Series(test_pre2) + w[2] * pd.Series(test_pre3)
return weighted_result
# 根据各模型的预测结果计算MAE
'''
metrics.mean_absolute_error - 多维数组MAE的计算方法
'''
print('Pred1 MAE:', metrics.mean_absolute_error(y_test_true, test_pre1))
print('Pred2 MAE:', metrics.mean_absolute_error(y_test_true, test_pre2))
print('Pred3 MAE:', metrics.mean_absolute_error(y_test_true, test_pre3))
Pred1 MAE: 0.1750000000000001
Pred2 MAE: 0.07499999999999993
Pred3 MAE: 0.10000000000000009
# 根据加权计算MAE
## 定义比重权值
w = [0.3, 0.4, 0.3]
weighted_pre = weighted_method(test_pre1, test_pre2, test_pre3, w)
print('Weighted_pre MAE:', metrics.mean_absolute_error(y_test_true, weighted_pre))
Weighted_pre MAE: 0.05750000000000027
# 定义结果的加权平均函数 - mean平均
def mean_method(test_pre1, test_pre2, test_pre3):
mean_result = pd.concat([pd.Series(test_pre1),
pd.Series(test_pre2),
pd.Series(test_pre3)], axis=1).mean(axis=1)
return mean_result
# 根据均值计算MAE
Mean_pre = mean_method(test_pre1, test_pre2, test_pre3)
print('Mean_pre MAE:', metrics.mean_absolute_error(y_test_true, Mean_pre))
Mean_pre MAE: 0.06666666666666693
# 定义结果的加权平均函数 - median平均
def median_method(test_pre1, test_pre2, test_pre3):
median_result = pd.concat([pd.Series(test_pre1),
pd.Series(test_pre2),
pd.Series(test_pre3)], axis=1).median(axis=1)
return median_result
# 根据中位数计算MAE
Median_pre = median_method(test_pre1, test_pre2, test_pre3)
print('Median_pre MAE:', metrics.mean_absolute_error(y_test_true, Median_pre))
Median_pre MAE: 0.07500000000000007
# Stacking融合(回归)
# 定义Stacking融合函数
def Stacking_method(train_reg1, train_reg2, train_reg3,
y_train_true,
test_pre1, test_pre2, test_pre3,
model_L2=linear_model.LinearRegression()):
'''
:param train_reg1: 第一个模型预测train得到的标签
:param train_reg2: 第二个模型预测train得到的标签
:param train_reg3: 第三个模型预测train得到的标签
:param y_train_true: train真实的标签
:param test_pre1: 第一个模型预测test得到的标签
:param test_pre2: 第二个模型预测test得到的标签
:param test_pre3: 第三个模型预测test得到的标签
:param model_L2: 次级模型:以真实训练集的标签为标签,以多个模型训练训练集后得到的标签合并后的数据集为特征进行训练
注意:次级模型不宜选取的太复杂,这样会导致模型在训练集上过拟合,测试集泛化效果差
:return: 训练好的次机模型预测test数据集得到的预测值 - Stacking_result
'''
model_L2.fit(pd.concat([pd.Series(train_reg1), pd.Series(train_reg2), pd.Series(train_reg3)], axis=1).values,
y_train_true) # 次级模型训练
stacking_result = model_L2.predict(pd.concat([pd.Series(test_pre1),
pd.Series(test_pre2), pd.Series(test_pre3)], axis=1).values)
return stacking_result
# 生成一些简单的样本数据,test_prei代表第i个模型的预测值,y_test_true代表模型的真实值
train_reg1 = [3.2, 8.2, 9.1, 5.2]
train_reg2 = [2.9, 8.1, 9.0, 4.9]
train_reg3 = [3.1, 7.9, 9.2, 5.0]
y_train_true = [3, 8, 9, 5]
test_pre1 = [1.2, 3.2, 2.1, 6.2]
test_pre2 = [0.9, 3.1, 2.0, 5.9]
test_pre3 = [1.1, 2.9, 2.2, 6.0]
y_test_true = [1, 3, 2, 6]
# 看一下Stacking融合的效果
model_L2 = linear_model.LinearRegression() # 不设定这个参数也可以,创建函数的时候默认了
Stacking_pre = Stacking_method(train_reg1, train_reg2, train_reg3, y_train_true,
test_pre1, test_pre2, test_pre3, model_L2)
print('Stacking_pre MAE: ', metrics.mean_absolute_error(y_test_true, Stacking_pre))
Stacking_pre MAE: 0.042134831460675204
# 发现模型效果相对于之前有了更近一步的提升
# 分类模型融合 - Voting,Stacking…
# Voting投票机制
'''
Voting - 投票机制
1.硬投票 - 对多个模型直接进行投票,不区分模型结果的相对重要度,最终投票数最多的类为最终被预测的类
2.软投票 - 和硬投票原理相同,增加了设置权重的功能,可以为不同模型设置不同权重,进而区别模型不同的重要度
'''
# # 硬投票
iris = datasets.load_iris() # 读取鸢尾花数据集 - 分类问题
x = iris.data # 分离特征集和标签
y = iris.target
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3) # 训练集和测试集按照7:3比例切分
# 用XGB分类模型训练数据
'''
colsample_bytree - 训练每棵树时,使用的特征占全部特征的比例
objective - 目标函数
二分类问题 - binary:logistic - 返回概率
'''
clf1 = XGBClassifier(learning_rate=0.1, n_estimators=150, max_depth=3, min_child_weight=2, subsample=0.7,
colsample_bytree=0.6, objective='binary:logistic')
# 用随机森林分类模型训练数据
'''
n_estimators - 随机森林中决策树的个数
max_depth - 决策树的最大深度
如果值为None,那么会扩展节点,直到所有的叶子是纯净的,或者直到所有叶子包含少于min_sample_split的样本
min_samples_split - 分割内部节点所需要的最小样本数量
min_samples_leaf - 需要在叶子结点上的最小样本数量
oob_score - 是否使用袋外样本来估计泛化精度
树的生成过程并不会使用所有的样本,未使用的样本就叫(out_of_bag)oob袋外样本,通过袋外样本,可以评估这个树的准确度
'''
clf2 = RandomForestClassifier(n_estimators=50, max_depth=1, min_samples_split=4,
min_samples_leaf=63, oob_score=True)
# 用SVC训练数据
'''
支持向量机 - 分类算法,但是也可以做回归,根据输入的数据不同可做不同的模型
1.若输入标签为连续值则做回归
2.若输入标签为分类值则用SVC()做分类
支持向量机的学习策略是间隔最大化,最终可转化为一个凸二次规划问题的求解
参数详解:
C - 惩罚参数; 值越大,对误分类的惩罚大,不容犯错,于是训练集测试准确率高,但是泛化能力弱
值越小,对误分类的惩罚小,允许犯错,泛化能力较强
probability - 是否采用概率估计,默认为False
'''
clf3 = SVC(C=0.1)
# 硬投票
'''
eclf - 其实就是三个模型的集成算法,硬投票决定最终被预测的类
'''
eclf = VotingClassifier(estimators=[('xgb', clf1), ('rf', clf2), ('svc', clf3)], voting='hard') # 本质是Ensemble
for clf, label in zip([clf1, clf2, clf3, eclf], ['XGBBoosting', 'Random Forest', 'SVM', 'Ensemble']):
scores = cross_val_score(clf, x, y, cv=5, scoring='accuracy') # 以准确度度量评分
print('Accuracy: %0.2f (+/- %0.2f) [%s]' % (scores.mean(), scores.std(), label))
Accuracy: 0.96 (+/- 0.02) [XGBBoosting]
Accuracy: 0.33 (+/- 0.00) [Random Forest]
Accuracy: 0.92 (+/- 0.03) [SVM]
Accuracy: 0.95 (+/- 0.05) [Ensemble]
# 软投票
x = iris.data
y = iris.target
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3)
clf1 = XGBClassifier(learning_rate=0.1, n_estimators=150, max_depth=3, min_child_weight=2, subsample=0.8,
colsample_bytree=0.8, objective='binary:logistic')
clf2 = RandomForestClassifier(n_estimators=50, max_depth=1, min_samples_split=4,
min_samples_leaf=63, oob_score=True)
clf3 = SVC(C=0.1, probability=True)
eclf = VotingClassifier(estimators=[('xgb', clf1), ('rf', clf2), ('svc', clf3)], voting='soft', weights=[2, 1, 1])
for clf, label in zip([clf1, clf2, clf3, eclf], ['XGBBoosting', 'Random Forest', 'SVM', 'Ensemble']):
scores = cross_val_score(clf, x, y, cv=5, scoring='accuracy') # 以准确度度量评分
print('Accuracy: %0.2f (+/- %0.2f) [%s]' % (scores.mean(), scores.std(), label))
Accuracy: 0.96 (+/- 0.02) [XGBBoosting]
Accuracy: 0.33 (+/- 0.00) [Random Forest]
Accuracy: 0.92 (+/- 0.03) [SVM]
Accuracy: 0.96 (+/- 0.02) [Ensemble]
# 分类的Stacking/Blending融合
'''
Stacking是一种分层模型集成框架,以两层为例
第一层由多个基学习器组成,其输入为原始训练集
第二层的模型则是以第一层学习器的输出作为训练集进行再训练,从而得到完整的stacking模型
'''
# ## 创建训练用的数据集
data_0 = iris.data
data = data_0[:100, :] # 100个样本
target_0 = iris.target
target = target_0[:100]
# ## 模型融合中使用到的各个单模型
'''
LogisticRegression()
solver - 用来优化权重 {‘lbfgs’, ‘sgd’, ‘adam’},默认adam,
lbfgs - quasi-Newton方法的优化器:对小数据集来说,lbfgs收敛更快效果也更好
sgd - 随机梯度下降
adam - 机遇随机梯度的优化器
RandomForestClassifier()
n_estimators - 决策树个数
n_jobs - 用于拟合和预测的并行运行的工作数量,如果值为-1,那么工作数量被设置为核的数量
criterion - 衡量分裂质量的性能
1.gini - Gini impurity衡量的是从一个集合中随机选择一个元素
基于该集合中标签的概率分布为元素分配标签的错误率
Gini impurity的计算就非常简单了,即1减去所有分类正确的概率,得到的就是分类不正确的概率
若元素数量非常多,且所有元素单独属于一个分类时,Gini不纯度达到极小值0
2.entropy - 信息增益熵
ExtraTreesClassifier() - 极端随机树
该算法与随机森林算法十分相似,都是由许多决策树构成,但该算法与随机森林有两点主要的区别:
1.随机森林应用的是Bagging模型,而ET是使用所有的训练样本得到每棵决策树,也就是每棵决策树应用的是相同的全部训练样本
关于Bagging和Boosting的差别,可以参考 https://www.cnblogs.com/earendil/p/8872001.html
2.随机森林是在一个随机子集内得到最佳分叉属性,而ET是完全随机的得到分叉值,从而实现对决策树进行分叉的
Gradient Boosting - 迭代的时候选择梯度下降的方向来保证最后的结果最好
损失函数用来描述模型的'靠谱'程度,假设模型没有过拟合,损失函数越大,模型的错误率越高
如果我们的模型能够让损失函数持续的下降,最好的方式就是让损失函数在其梯度方向下降
GradientBoostingRegressor()
loss - 选择损失函数,默认值为ls(least squres),即最小二乘法,对函数拟合
1.lad - 绝对损失
2.huber - Huber损失
3.quantile - 分位数损失
4.ls - 均方差损失(默认)
learning_rate - 学习率
n_estimators - 弱学习器的数目,默认值100
max_depth - 每一个学习器的最大深度,限制回归树的节点数目,默认为3
min_samples_split - 可以划分为内部节点的最小样本数,默认为2
min_samples_leaf - 叶节点所需的最小样本数,默认为1
alpha - 当我们使用Huber损失和分位数损失'quantile'时,需要指定分位数的值,只有regressor有
GradientBoostingClassifier() - 参数绝大多数和Regressor相同,不同的是loss函数
1.deviance - 对数似然损失函数(默认)
2.exponential - 指数损失函数
参考网址: https://www.cnblogs.com/pinard/p/6143927.html
'''
clfs = [LogisticRegression(solver='lbfgs'),
RandomForestClassifier(n_estimators=5, n_jobs=-1, criterion='gini'),
ExtraTreesClassifier(n_estimators=5, n_jobs=-1, criterion='gini'),
ExtraTreesClassifier(n_estimators=5, n_jobs=-1, criterion='entropy'),
GradientBoostingClassifier(learning_rate=0.05, subsample=0.5, max_depth=6, n_estimators=5)]
# ## 切分一部分数据作为测试集
X, X_predict, y, y_predict = train_test_split(data, target, test_size=0.3, random_state=2020)
dataset_blend_train = np.zeros((X.shape[0], len(clfs))) # 全零数组,行取训练集的个数,列取模型个数
dataset_blend_test = np.zeros((X_predict.shape[0], len(clfs))) # 全零数组,行取测试集的个数,列取模型个数
# 5折Stacking - 即每次Stacking训练都会在第一层基学习器进行5折交叉验证,再进入第二层学习器训练
n_splits = 5
skf = StratifiedKFold(n_splits) # # 分层交叉验证,每一折中都保持着原始数据中各个类别的比例关系(测试集和训练集分离)
skf = skf.split(X, y) # 把特征和标签分离
'''
enumerate() - 用于将一个可遍历的数据对象(如列表、元组或字符串)组合为一个索引序列,同时列出数据和数据下标,一般用在for循环当中
'''
for j, clf in enumerate(clfs):
# 依次训练各个单模型
dataset_blend_test_j = np.zeros((X_predict.shape[0], len(clfs))) # 30行5列的全0数组
# 五折交叉训练,使用第i个部分作为预测集,剩余部分为验证集,获得的预测值成为第i部分的新特征
for i, (train, test) in enumerate(skf):
X_train, y_train, X_test, y_test = X[train], y[train], X[test], y[test]
clf.fit(X_train, y_train)
# 将对测试集的概率预测第二列(也就是结果为1)的概率装进y_submission中
y_submission = clf.predict_proba(X_test)[:, 1]
dataset_blend_train[test, j] = y_submission # 把预测验证集(比如第一折)的结果依次对应装进dataset_blend_train中
'''
predict_proba() - 返回的是一个n行k列的数组
第i行第j列上的数值是模型预测第i个预测样本为某个标签的概率,并且每一行的概率和为1
'''
'''
因为我们采取到的数据集的标签只有0或1,所以predict_proba返回的概率只有两个
如果左边的概率大于0.5,那么预测值为0
如果右边的概率大于0.5,那么预测值为1
'''
# # 将对测试集的概率预测的第二列(也就是结果为1)的概率装进dataset_blend_test_j中
dataset_blend_test_j[:, i] = clf.predict_proba(X_predict)[:, 1]
# 对于测试集,直接用这5个模型的预测值均值作为新的特征
dataset_blend_test[:, j] = dataset_blend_test_j.mean(1) # mean(1) - 求每行数的平均值(五折预测测试集的平均值)
print('val auc Score: %f' % roc_auc_score(y_predict, dataset_blend_test[:, j]))
clf = LogisticRegression(solver='lbfgs') # 次级学习器再次训练
clf.fit(dataset_blend_train, y) # 把第一层得到训练集的预测结果作为新特征,把训练集的真实标签作为标签,进行第二层训练
y_submission = clf.predict_proba(dataset_blend_test)[:, 1] # 把第一层预测测试集的结果作为新特征,预测测试集的标签
'''
ROC曲线和AUC - 用来评价一个二值分类器(binary classifier)的优劣,用于衡量'二分类问题'机器学习算法性能(泛化能力)
AUC - ROC曲线下的面积
AUC的取值范围在0.5和1之间
使用AUC值作为评价标准是因为很多时候ROC曲线并不能清晰的说明哪个分类器的效果更好
而作为一个数值,对应AUC更大的分类器效果更好
'''
print('Val auc Score of Stacking: %f' % (roc_auc_score(y_predict, y_submission)))
val auc Score: 1.000000
val auc Score: 0.500000
val auc Score: 0.500000
val auc Score: 0.500000
val auc Score: 0.500000
Val auc Score of Stacking: 1.000000
# Blending - 和Stacking类似,不同点在于:
'''
1.Stacking - 把第一层得到训练集的预测结果作为新特征,把训练集的真实标签作为标签,进行第二层训练
2.Blending - 把第一层得到训练集中的30%的验证集的结果作为新特征继续训练,把训练集的真实标签作为标签,进行第二层训练
Blending优点 - 比stacking简单,因为不用进行k次的交叉验证来获得stacker feature
避开了一个信息泄露问题:generlizers和stacker使用了不一样的数据集
Blending缺点- 使用了很少的数据,可能会过拟合,没有stacking使用多次的交叉验证来的稳健
'''
data_0 = iris.data
data = data_0[:100, :]
target_0 = iris.target
target = target_0[:100]
clfs = [LogisticRegression(solver='lbfgs'),
RandomForestClassifier(n_estimators=5, n_jobs=-1, criterion='gini'),
RandomForestClassifier(n_estimators=5, n_jobs=-1, criterion='entropy'),
ExtraTreesClassifier(n_estimators=5, n_jobs=-1, criterion='gini'),
GradientBoostingClassifier(learning_rate=0.05, subsample=0.5, max_depth=6, n_estimators=5)]
# 划分训练集和测试集
X, X_predict, y, y_predict = train_test_split(data, target, test_size=0.3, random_state=2020)
# 把训练数据分成d1(子训练集),d2(验证集)两部分 - 对半分
X_d1, X_d2, y_d1, y_d2 = train_test_split(X, y, test_size=0.5, random_state=2020)
dataset_d1 = np.zeros((X_d2.shape[0], len(clfs))) # 35行5列的全0数组
dataset_d2 = np.zeros((X_predict.shape[0], len(clfs))) # 30行5列的全0数组
for j, clf in enumerate(clfs):
# 用子训练集依次训练各个模型
clf.fit(X_d1, y_d1)
# 返回模型对验证集的预测值为1的概率
y_submission = clf.predict_proba(X_d2)[:, 1]
# 结果装进dataset_d1中 - 表示用子训练集训练的模型预测验证集标签的结果 - 就是上文说的30%的数据
dataset_d1[:, j] = y_submission
# 建立第二层模型的特征 - 用第一层模型预测测试集的结果作为新的特征
dataset_d2[:, j] = clf.predict_proba(X_predict)[:, 1]
# 看一下预测的预测集标签和真实的预测集标签的roc_auc_score
print('val auc Score: %f' % roc_auc_score(y_predict, dataset_d2[:, j]))
# 用第二层模型训练特征
clf = GradientBoostingClassifier(learning_rate=0.02, subsample=0.5, max_depth=6, n_estimators=30)
clf.fit(dataset_d1, y_d2) # 用验证集的第一层模型预测结果作为特征,用验证集的真实标签作为标签,再次训练
y_submission = clf.predict_proba(dataset_d2)[:, 1] # 用第一层模型预测测试集的结果作为特征,用第二层模型预测训练集返回1的概率
print('Val auc Score of Blending: %f' % (roc_auc_score(y_predict, y_submission)))
val auc Score: 1.000000
val auc Score: 1.000000
val auc Score: 1.000000
val auc Score: 1.000000
val auc Score: 1.000000
Val auc Score of Blending: 1.000000
# 利用mlxtend进行分类的Stacking融合
iris = datasets.load_iris()
X, y = iris.data[:, 1:3], iris.target
clf1 = KNeighborsClassifier(n_neighbors=1)
clf2 = RandomForestClassifier(random_state=1)
clf3 = GaussianNB()
lr = LogisticRegression()
'''
StackingClassifier() - 快速Stacking融合的方法
参数详解:
classifiers - 一级分类器列表
meta_classifier - 二级分类器(元分类器)
use_probas - 如果为True,则基于预测的概率而不是类标签来训练元分类器,默认为False
average_probas - 如果为真,将概率平均为元特征,默认为False
verbose - 是否输出到日志
'''
sclf = StackingClassifier(classifiers=[clf1, clf2, clf3],
meta_classifier=lr)
label = ['KNN', 'Random Forest', 'Naive Bayes', 'Stacking Classifier']
clf_list = [clf1, clf2, clf3, sclf]
fig = plt.figure(figsize=(10, 8))
gs = gridspec.GridSpec(2, 2) # 网格布局,每行2个,每列2个
grid = itertools.product([0, 1], repeat=2) # 求多个可迭代对象的笛卡尔积,其实就是更加灵活调整网格的大小
clf_cv_mean = [] # 存放每个模型的准确率的均值
clf_cv_std = [] # 存放每个模型的准确率的标准差
for clf, label, grd in zip(clf_list, label, grid):
scores = cross_val_score(clf, X, y, cv=3, scoring='accuracy') # 3折交叉验证,评分标准为模型准确率
print('Accuracy: %.2f (+/- %.2f) [%s]' % (scores.mean(), scores.std(), label))
clf_cv_mean.append(scores.mean())
clf_cv_std.append(scores.std())
clf.fit(X, y)
ax = plt.subplot(gs[grd[0], grd[1]])
fig = plot_decision_regions(X=X, y=y, clf=clf)
plt.title(label)
plt.show()
Accuracy: 0.91 (+/- 0.01) [KNN]
Accuracy: 0.95 (+/- 0.01) [Random Forest]
Accuracy: 0.91 (+/- 0.02) [Naive Bayes]
Accuracy: 0.95 (+/- 0.02) [Stacking Classifier]
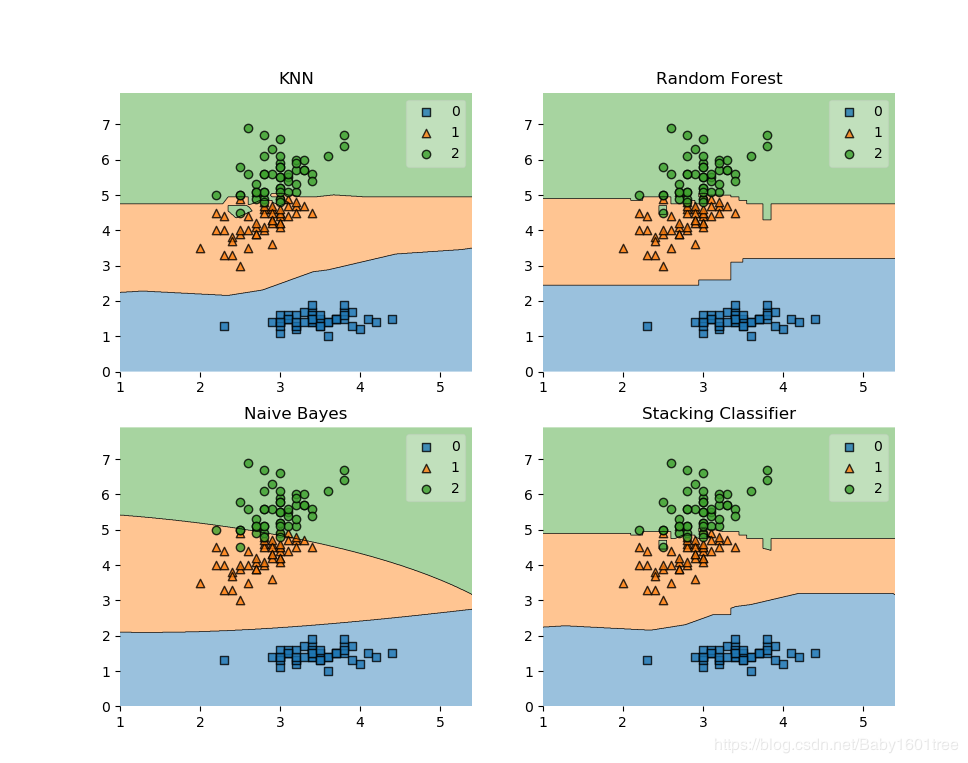
可以看出,融合后的曲线更加优秀
'''
将特征放进模型中预测,并将预测结果变换并作为新的特征加入原有特征中,再经过模型预测结果(Stacking变化)
可以反复预测多次将结果加入最后的特征中
'''
def ensemble_add_feature(train, test, target, clfs):
# n_folds = 5
# skf = list(StratifiedKFold(y, n_folds=n_folds))
train_ = np.zeros((train.shape[0], len(clfs * 2)))
test_ = np.zeros((test.shape[0], len(clfs * 2)))
for j, clf in enumerate(clfs):
# 依次训练单个模型
print(j, clf)
# 使用第1部分作为预测,第2部分来训练模型(第1部分预测的输出作为第2部分的新特征)
# X_train, y_train, X_test, y_test = X[train], y[train]
clf.fit(train, target) # 训练模型
y_train = clf.predict(train) # 模型在训练集中的预测值
y_test = clf.predict(test) # 模型在测试集中的预测值
# 生成新特征
'''
j 从0开始递增,构建新的特征集,特征为训练集和测试集各自的预测值的平方
'''
train_[:, j*2] = y_train ** 2
test_[:, j*2] = y_test ** 2
train_[:, j+1] = np.exp(y_train) # np.exp(a) - 返回e的a次方
test_[:, j+1] = np.exp(y_test)
print('Method:', j)
train_ = pd.DataFrame(train_)
test_ = pd.DataFrame(test_)
return train_, test_
clf = LogisticRegression() # 次级模型
data_0 = iris.data
data = data_0[:100, :]
target_0 = iris.target
target = target_0[:100]
x_train, x_test, y_train, y_test = train_test_split(data, target, test_size=0.3)
x_train = pd.DataFrame(x_train) # 转换成DataFrame格式,方便后续构造新特征
x_test = pd.DataFrame(x_test)
# 给出模型融合中使用到的各个单模型
clfs = [LogisticRegression(),
RandomForestClassifier(n_estimators=5, n_jobs=-1, criterion='gini'),
ExtraTreesClassifier(n_estimators=5, n_jobs=-1, criterion='gini'),
ExtraTreesClassifier(n_estimators=5, n_jobs=-1, criterion='entropy'),
GradientBoostingClassifier(learning_rate=0.05, subsample=0.5, max_depth=6, n_estimators=5)]
# 新特征的构造 - 用上面的各个单模型预测训练集和测试集的结果,作为新特征
New_train, New_test = ensemble_add_feature(x_train, x_test, y_train, clfs)
clf.fit(New_train, y_train) # 用训练集的新特征和训练集的真实标签训练数据
y_emb = clf.predict_proba(New_test)[:, 1] # 用训练好的模型得到新的测试集特征返回1的概率
print('Val auc Score of Stacking: %f' % (roc_auc_score(y_test, y_emb)))
Method: 4
Val auc Score of Stacking: 1.000000
本赛题示例
# 数据读取
Train_data = pd.read_csv(r'F:\Users\TreeFei\文档\PyC\ML_Used_car\data\used_car_train_20200313.csv', sep=' ')
TestA_data = pd.read_csv(r'F:\Users\TreeFei\文档\PyC\ML_Used_car\data\used_car_testA_20200313.csv', sep=' ')
print(Train_data.shape)
print(TestA_data.shape)
# 回顾一下数据
Train_data.head()
Train_data.info() # 20个浮点类型字段,10个整数型字段,1个object字段
'''
通过info(),训练集发现一共有4个字段有缺失值
model字段有1个缺失值
bodyType字段有4506个缺失值
fuelType字段有8680个缺失值
gearbox字段有5981个缺失值
'''
# 我们把数值型字段和非数值型字段做一个区分
numerical_cols = Train_data.select_dtypes(exclude='object').columns # 这是所有数值类型的字段
print(numerical_cols)
# 其中SaleID(合同号),name(汽车交易名称),regDate(汽车注册时间)三个字段看似没有用处,暂时抛弃这些特征
# price是标签字段,不放在特征集中
feature_cols = [col for col in numerical_cols if col not in ['SaleID', 'name', 'regDate', 'price']]
# 区分特征集和标签集
X_data = Train_data[feature_cols]
Y_data = Train_data['price']
X_test = TestA_data[feature_cols]
print('X train shape:', X_data.shape)
print('X test shape:', X_test.shape)
X train shape: (150000, 26)
X test shape: (50000, 26)
# 创建一个统计函数,方便后续信息统计
def sta_inf(data):
print('_min:', np.min(data))
print('_max:', np.max(data))
print('_mean:', np.mean(data))
print('_ptp:', np.ptp(data)) # ptp - 最大值和最小值的差值
print('_std:', np.std(data))
print('_var:', np.var(data))
print('Sta of label', sta_inf(Y_data)) # 看一下训练集标签的统计分布
_min: 11
_max: 99999
_mean: 5923.327333333334
_ptp: 99988
_std: 7501.973469876438
_var: 56279605.94272992
# 简单填补训练集和测试集的缺失值 - 用-1填充
X_data = X_data.fillna(-1)
X_test = X_test.fillna(-1)
# 为了代码简洁,创建好模型训练函数
# ## 线性回归
def build_model_lr(x_train, y_train):
reg_model = linear_model.LinearRegression()
reg_model.fit(x_train, y_train)
return reg_model
# ## Ridge 岭回归 - 加入了l2正则化的线性回归
'''
L2正则化 - 岭回归 - 模型被限制在圆形区域(二维区域下),损失函数的最小值因为圆形约束没有角,所以不会使得权重为0,但是可以使得权重
都尽可能的小,最后得到一个所有参数都比较小的模型,这样模型比较简单,能适应不同数据集,一定程度上避免了过拟合
'''
def build_model_ridge(x_train, y_train):
reg_model = linear_model.Ridge(alpha=0.8) # alpha - 正则化系数
reg_model.fit(x_train, y_train)
return reg_model
# ## Lasso回归 - 加入了l1正则化的线性回归
'''
L1正则化 - Lasso回归 - 模型被限制在正方形区域(二维区域下),损失函数的最小值往往在正方形(约束)的角上,很多权值为0(多维),所以可以
实现模型的稀疏性(生成稀疏权值矩阵,进而用于特征选择
'''
def build_model_lasso(x_train, y_train):
reg_model = linear_model.LassoCV()
reg_model.fit(x_train, y_train)
return reg_model
# ## gbdt -梯度下降树 - 传统机器学习算法里面是对真实分布拟合的最好的几种算法之一
'''
Boosting算法思想 - 一堆弱分类器的组合就可以成为一个强分类器;
不断地在错误中学习,迭代来降低犯错概率
通过一系列的迭代来优化分类结果,每迭代一次引入一个弱分类器,来克服现在已经存在的弱分类器组合的短板
Adaboost - 整个训练集上维护一个分布权值向量W
用赋予权重的训练集通过弱分类算法产生分类假设(基学习器)y(x)
然后计算错误率,用得到的错误率去更新分布权值向量w
对错误分类的样本分配更大的权值,正确分类的样本赋予更小的权值
每次更新后用相同的弱分类算法产生新的分类假设,这些分类假设的序列构成多分类器
对这些多分类器用加权的方法进行联合,最后得到决策结果
Gradient Boosting - 迭代的时候选择梯度下降的方向来保证最后的结果最好
损失函数用来描述模型的'靠谱'程度,假设模型没有过拟合,损失函数越大,模型的错误率越高
如果我们的模型能够让损失函数持续的下降,最好的方式就是让损失函数在其梯度方向下降
GradientBoostingRegressor()
loss - 选择损失函数,默认值为ls(least squres),即最小二乘法,对函数拟合
learning_rate - 学习率
n_estimators - 弱学习器的数目,默认值100
max_depth - 每一个学习器的最大深度,限制回归树的节点数目,默认为3
min_samples_split - 可以划分为内部节点的最小样本数,默认为2
min_samples_leaf - 叶节点所需的最小样本数,默认为1
参考资料:https://www.cnblogs.com/zhubinwang/p/5170087.html
'''
def build_model_gbdt(x_train, y_train):
estimator = GradientBoostingRegressor(loss='ls', subsample=0.85, max_depth=5, n_estimators=100)
param_grid = {'learning_rate': [0.05, 0.08, 0.1, 0.2]}
gbdt = GridSearchCV(estimator, param_grid, cv=3) # 网格搜索最佳参数,3折交叉检验
gbdt.fit(x_train, y_train)
print(gbdt.best_params_) # 输出最佳参数
print(gbdt.best_estimator_)
return gbdt
# ## xgb - 梯度提升决策树
'''
XGBRegressor - 梯度提升回归树,也叫梯度提升机
采用连续的方式构造树,每棵树都试图纠正前一棵树的错误
与随机森林不同,梯度提升回归树没有使用随机化,而是用到了强预剪枝
从而使得梯度提升树往往深度很小,这样模型占用的内存少,预测的速度也快
gamma - 定了节点分裂所需的最小损失函数下降值,这个参数的值越大,算法越保守
subsample - 这个参数控制对于每棵树随机采样的比例,减小这个参数的值,算法会更加保守,避免过拟合
colsample_bytree - 用来控制每棵随机采样的列数的占比
learning_rate - 学习速率,用于控制树的权重,xgb模型在进行完每一轮迭代之后,会将叶子节点的分数乘上该系数,
以便于削弱各棵树的影响,避免过拟合
'''
def build_model_xgb(x_train, y_train):
model = xgb.XGBRegressor(n_estimators=120, learning_rate=0.08, gamma=0,
subsample=0.8, colsample_bytree=0.9, max_depth=5)
model.fit(x_train, y_train)
return model
# ## lgb - xgb加强版
''''
LightGBM - 使用的是histogram算法,占用的内存更低,数据分隔的复杂度更低
思想是将连续的浮点特征离散成k个离散值,并构造宽度为k的Histogram
然后遍历训练数据,统计每个离散值在直方图中的累计统计量
在进行特征选择时,只需要根据直方图的离散值,遍历寻找最优的分割点
LightGBM采用leaf-wise生长策略:
每次从当前所有叶子中找到分裂增益最大(一般也是数据量最大)的一个叶子,然后分裂,如此循环。
因此同Level-wise相比,在分裂次数相同的情况下,Leaf-wise可以降低更多的误差,得到更好的精度
Leaf-wise的缺点是可能会长出比较深的决策树,产生过拟合
因此LightGBM在Leaf-wise之上增加了一个最大深度的限制,在保证高效率的同时防止过拟合
参数:
num_leaves - 控制了叶节点的数目,它是控制树模型复杂度的主要参数,取值应 <= 2 ^(max_depth)
bagging_fraction - 每次迭代时用的数据比例,用于加快训练速度和减小过拟合
feature_fraction - 每次迭代时用的特征比例,例如为0.8时,意味着在每次迭代中随机选择80%的参数来建树,
boosting为random forest时用
min_data_in_leaf - 每个叶节点的最少样本数量。
它是处理leaf-wise树的过拟合的重要参数
将它设为较大的值,可以避免生成一个过深的树。但是也可能导致欠拟合
max_depth - 控制了树的最大深度,该参数可以显式的限制树的深度
n_estimators - 分多少颗决策树(总共迭代的次数)
objective - 问题类型
regression - 回归任务,使用L2损失函数
regression_l1 - 回归任务,使用L1损失函数
huber - 回归任务,使用huber损失函数
fair - 回归任务,使用fair损失函数
mape (mean_absolute_precentage_error) - 回归任务,使用MAPE损失函数
'''
def build_model_lgb(x_train, y_train):
estimator = lgb.LGBMRegressor(num_leaves=63, n_estimators=100)
param_grid = {'learning_rate': [0.01, 0.05, 0.1]}
gbm = GridSearchCV(estimator, param_grid)
gbm.fit(x_train, y_train)
print(gbm.best_params_)
return gbm
# XGB的五折交叉回归验证 - 这里只是举例,别的模型也可以这么验证
xgr = xgb.XGBRegressor(n_estimators=120, learning_rate=0.1, subsample=0.8, colsample_bytree=0.9, max_depth=7)
scores_train = [] # 每次模型训练训练集中子训练集的得分
scores = [] # 每次模型训练训练集中验证集的得分
sk = StratifiedKFold(n_splits=5, shuffle=True, random_state=0) # shuffle判断是否在每次抽样时对样本进行清洗
for train_ind, val_ind in sk.split(X_data, Y_data):
train_x = X_data.iloc[train_ind].values
train_y = Y_data.iloc[train_ind]
val_x = X_data.iloc[val_ind].values
val_y = Y_data.iloc[val_ind]
xgr.fit(train_x, train_y)
pred_train_xgb = xgr.predict(train_x) # 子训练集的预测值
pre_xgb = xgr.predict(val_x) # 验证集的预测值
score_train = mean_absolute_error(train_y, pred_train_xgb)
scores_train.append(score_train) # 统计子训练集的mae
score = mean_absolute_error(val_y, pre_xgb)
scores.append(score) # 统计验证集的mae
print('Train mae:', np.mean(scores_train)) # 统计mae均值
print('Val mae:', np.mean(scores))
因为跑的很慢,所以记录一下这次的结果
Train mae: 596.3128886185606
Val mae: 693.382067947197
x_train, x_val, y_train, y_val = train_test_split(X_data, Y_data, test_size=0.3)
# ## 训练并预测
print('Predict LR...')
model_lr = build_model_lr(x_train, y_train)
val_lr = model_lr.predict(x_val) # 得到验证集的预测值
subA_lr = model_lr.predict(X_test)
print('Predict Ridge...')
model_ridge = build_model_ridge(x_train, y_train)
val_ridge = model_ridge.predict(x_val)
subA_ridge = model_ridge.predict(X_test)
print('Predict Lasso...')
model_lasso = build_model_lasso(x_train, y_train)
val_lasso = model_lasso.predict(x_val)
subA_lasso = model_lasso.predict(X_test)
print('Predict GBDT...')
model_gbdt = build_model_gbdt(x_train, y_train)
val_gbdt = model_gbdt.predict(x_val)
subA_gbdt = model_gbdt.predict(X_test)
Predict LR...
Predict Ridge...
Predict Lasso...
Predict GBDT...
{'learning_rate': 0.2}
因为GBDT加了网格搜索调参,所以跑的特别慢…
# 一般比赛中效果最为显著的两种方法 - XGB/LGBprint('Predict XGB...')
model_xgb = build_model_xgb(x_train, y_train)
val_xgb = model_xgb.predict(x_val)
subA_xgb = model_xgb.predict(X_test)
print('Predict LGB...')
model_lgb = build_model_lgb(x_train, y_train)
val_lgb = model_lgb.predict(x_val)
subA_lgb = model_lgb.predict(X_test)
{'learning_rate': 0.1}
# ## 看一下lgb模型预测测试集的数据统计性分布
print('Sta inf of lgb:', sta_inf(subA_lgb))
_min: -76.40857341373585
_max: 88951.1857499891
_mean: 5926.870646241635
_ptp: 89027.59432340284
_std: 7379.389534056081
_var: 54455389.89533643
# 加权融合 - 简单加权平均
# ## 使用我们定义过的加权平均函数weighted_method
# ## 设置权重
w = [0.3, 0.4, 0.3]
# ## 预测验证集的准确度 - 三个模型加权融合
val_pre = weighted_method(val_lgb, val_xgb, val_gbdt, w)
MAE_Weighted = mean_absolute_error(y_val, val_pre)
print('MAE of Weighted of val:', MAE_Weighted)
# 预测测试集的加权融合结果
subA = weighted_method(subA_lgb, subA_xgb, subA_gbdt, w)
MAE of Weighted of val: 724.2198039000299
# ## 看一下预测测试集融合后的结果统计分布
print('Sta inf:', sta_inf(subA))
_min: -878.0418803904766
_max: 88761.70460429232
_mean: 5931.043037628969
_ptp: 89639.7464846828
_std: 7367.855733884833
_var: 54285298.11533961
# ## 生成提交文件
sub = pd.DataFrame()
sub['SaleID'] = X_test.index
sub['price'] = subA
sub.to_csv(r'F:\Users\TreeFei\文档\PyC\ML_Used_car\data\sub_Weighted.csv', index=False)
# ##与简单的lr(线性回归)进行对比
val_lr_pred = model_lr.predict(x_val)
MAE_lr = mean_absolute_error(y_val, val_lr_pred)
print('MAE of lr:', MAE_lr)
lr_MAE:2588.26
#
weighted_MAE:724.84 —> 能看出,对比lr,加权融合之后模型的精确度有了非常大的提高
# Stacking融合# ## 第一层,得到各个单模型预测子训练集的预测值
train_lgb_pred = model_lgb.predict(x_train)
train_xgb_pred = model_xgb.predict(x_train)
train_gbdt_pred = model_gbdt.predict(x_train)
# ## 得到各个单模型预测验证集的预测值 --> 前面预测过了,直接拿来用
# ## 得到各个单模型预测测试集的预测值 --> 前面也预测过了,直接拿来用
# ## 创建新特征
Stark_X_train = pd.DataFrame() # 由子训练集的预测数据得到的新特征
Stark_X_train['Method_1'] = train_lgb_pred
Stark_X_train['Method_2'] = train_xgb_pred
Stark_X_train['Method_3'] = train_gbdt_pred
Stark_X_val = pd.DataFrame() # 由验证集的预测数据得到的新特征
Stark_X_val['Method_1'] = val_lgb
Stark_X_val['Method_2'] = val_xgb
Stark_X_val['Method_3'] = val_gbdt
Stark_X_test = pd.DataFrame() # 由测试集的预测数据得到的新特征
Stark_X_test['Method_1'] = subA_lgb
Stark_X_test['Method_2'] = subA_xgb
Stark_X_test['Method_3'] = subA_gbdt
# ## 第二层模型训练 - 元模型得简单一点,这里用线性回归
model_lr_Stacking = build_model_lr(Stark_X_train, y_train) # 用子训练集的新特征和标签训练
# ## 看模型在子训练集上的表现
train_pre_Stacking = model_lr_Stacking.predict(Stark_X_train)
print('MAE of Stacking-LR', mean_absolute_error(y_train, train_pre_Stacking))
MAE of Stacking-LR 630.5897643683384
# ## 看模型在验证集上的表现
val_pre_Stacking = model_lr_Stacking.predict(Stark_X_val)
print('MAE of Stacking-LR:', mean_absolute_error(y_val, val_pre_Stacking))
MAE of Stacking-LR: 722.2460136359339
# ## 预测测试集
print('Predict Stacking-LR...')
subA_Stacking = model_lr_Stacking.predict(Stark_X_test)
# 我们看一下预测值的统计性分布
sta_inf(subA_Stacking)
_min: -3638.174875620137
_max: 90457.25117154507
_mean: 5926.428386169822
_ptp: 94095.42604716521
_std: 7417.358806265995
_var: 55017211.6608917
# 有负值,我们去掉过小的预测值 - 预测值小于10的替换成10
subA_Stacking[subA_Stacking < 10] = 10
# 生成结果
sub = pd.DataFrame()
sub['SaleID'] = TestA_data.SaleID
sub['price'] = subA_Stacking
sub.to_csv(r'F:\Users\TreeFei\文档\PyC\ML_Used_car\data\sub_Stacking.csv', index=False)
# 提交两个结果之后,发现使用Stacking融合比使用加权融合效果好,但是还没有第一次baseline的分数理想
最后完整的比赛打算尝试从这些方面着重入手:
0.调整数据类型,压缩数据大小
1.测试集和训练集都有缺失值
2.notRepairedDamage有异常值,处理完记得转换成数值型特征
3.训练集标签分布呈现长尾分布,截断或log变换
4.箱线图处理训练集特征的异常数据
5.构造特征:使用时间 creatDate-regDate
errors='coerce’将不能转换的值变成nan,然后尝试用XGBOOST预测填补缺失值
6.邮编提取城市信息(二手车价格和城市可能有关)
7.根据品牌的销售统计量构造统计量特征
8.数据分桶 - 看下哪些特征是连续型的,变成离散型
9.使用SFS挑选最优特征
10.调参 - 贝叶斯调参
11.xgb,lgb加权融合
作者:恶魔眼睛大又大���