主成分分析（Principal Component Analysis，PCA）
文章目录1. 总体主成分分析2. 样本主成分分析3. 主成分分析方法3.1 相关矩阵的特征值分解算法3.2 矩阵奇异值分解算法4. sklearn.decomposition.PCA
主成分分析（Principal Component Analysis，PCA）是一种常用的无监督学习方法
利用正交变换把由
线性相关变量表示的观测数据 转换为 少数几个由线性无关变量表示的数据，线性无关的变量 称为 主成分
主成分的个数通常小于原始变量的个数，所以PCA属于降维方法
主要用于发现数据中的基本结构，即数据中变量之间的关系，是数据分析的有力工具，也用于其他机器学习方法的前处理
PCA属于多元统计分析的经典方法
1. 总体主成分分析
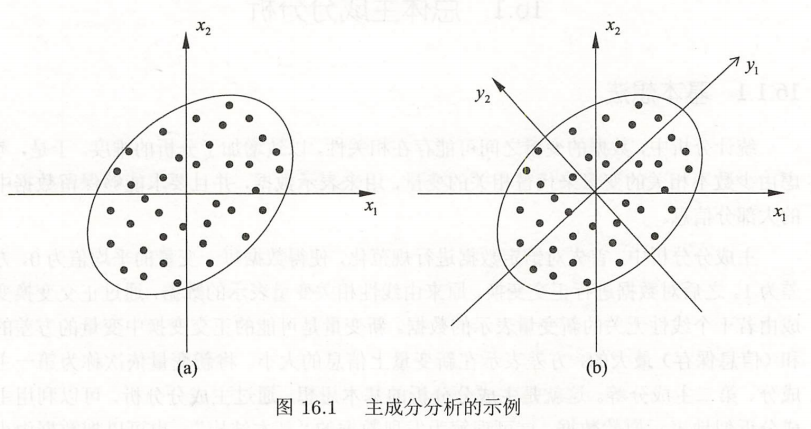
第一轴选取方差最大的轴 y1
原创文章 995获赞 3365访问量 52万+
关注
他的留言板
展开阅读全文
作者：Michael阿明
