无监督学习之PCA降维
无监督学习:通过无标签的数据,学习数据的分布或数据与数据之间的关系。
1. 降维算法1 定义:用低维的概念去类比高维的概念.将高维的图形转化为低维的图形的方法。
1.1. 算法模块 :PCA算法、NMF(非负矩阵分解)算法、LDA算法等。
1.2. Python库 :sklearn.decomposution;
1 主成分分析:主成分分析( Principal Component Analysis, PCA )是最常用的一种降维方法,通常用于高维数据集的探索与
可视化,还可以用作数据压缩和预处理等。PCA可以把具有相关性的高维变量合成为线性无关的低维变量,称为主成分。主成分能够尽可能保留原始数据的信息。
2 主成分分析步骤:
2.1 对原始数据标准化
2.2 计算相关系数
2.3 计算特征
2.4 确定主成分
2.5 合成主成分
3 相关数学术语:
3.1 方差
3.2 协方差
3.3 协方差矩阵
3.4 特征向量和特征值
4 主成分分析的主要作用:
4.1 主成分分析能降低所研究的数据空间的维数。
4.2 多维数据的一种图形表示方法。
4.3 由主成分分析法构造回归模型,可以把各主成分作为新自变量代替原来自变量x做回归分析。
4.4 有时可通过因子负荷Aij的结论,弄清各变量之间的某些关系。
方差:各个样本和样本均值的差的平方和的均值,用来度量一-组数据的分散程度。
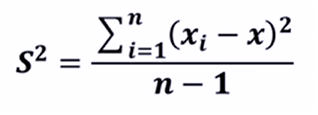
协方差:用于度量两个变量之间的线性相关性程度,若两个变量的协方差为0,则可认为二者线性无关。协方差矩阵则是由变量的协方差值构成的矩阵(对称阵)。
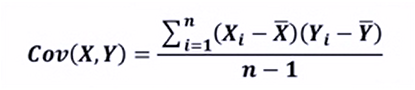
特征向量:矩阵的特征向量是描述数据集结构的非零向量
并满足如下公式:
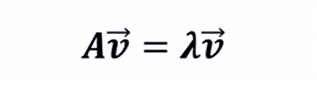
其中:A是方阵,v是特征向量,λ是特征值。
1 原理:
矩阵的主成分就是其协方差矩阵对应的特征向量,按照对应的特征值大小进行排序,最大的特征值就是第一主成分,其次是第二主成分,以此类推。
2 主成分分析-算法过程:

3 Python算法实现:
3.1. K-Means 模块的导入
#加载matplotlib用于数据的可视化
import matplotlib.pyplot as plt
#加载PCA算法包
from sklearn.decomposition import PCA
在sklearn库中,可以使用 sklearn.decomposition.PCA 加载PCA进行降维,主要参数有:
n_components:指定主成分的个数,即降维后数据的维度。 svd_solver:设置特征值分解的方法,默认为‘auto’,其他可选有‘full’, “arpack’, ‘randomized’。
3.2.数据的导入
Python中鸢尾花数据的导入
#加载鸢尾花数据集导入函数
from sklearn.datasets import load_iris
鸢尾花数据的部分展示:
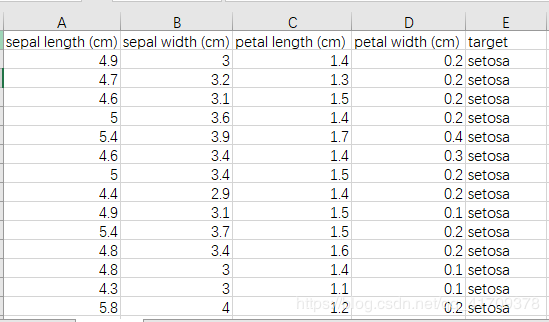
3.3. 实例程序编写
目标:实现高维数据可视化,已知鸢尾花数据是4维的,共三类样本。使用PCA实现对鸢尾花数据进行降维,实现在二维平面上的可视化。
Step 1 :加载数据并进行降维
#加载数据并进行降维
data = load_iris() #以字典的形式加载鸢尾花数据集
y = data.target #使用y表示数据集中的标签(类别)
x = data.data #使用x表示数据集中的属性数据
pca = PCA(n_components= 2) #设置降维后的主成分数目为2
reduced_x = pca.fit_transform(x) #对原始数据进行降维,并保存在reduced_x中
Step 2 :按类别对降维后的数据进行保存
#按类别对降维后的数据进行保存
red_x, red_y = [], [] #第一类数据点
blue_x, blue_y = [], [] #第二类数据点
green_x, green_y = [], [] #第三类数据点
def get_data(reduced_x, y):
'''
1.按照鸢尾花的类别将降维后的数据点保存在不同的列表中
'''
for i in range(len(reduced_x)):
if y[i] == 0:
red_x.append(reduced_x[i][0])
red_y.append(reduced_x[i][1])
elif y[i] == 1:
blue_x.append(reduced_x[i][0])
blue_y.append(reduced_x[i][1])
else:
green_x.append(reduced_x[i][0])
green_y.append(reduced_x[i][1])
Step 3 :降维后数据点的可视化
#对数据点的可视化
fig = plt.figure()
ax = fig.add_subplot()
plt.scatter(red_x, red_y, c='r', marker= 'x')
plt.scatter(blue_x, blue_y, c='b', marker= 'D')
plt.scatter(green_x, green_y, c='g', marker= '.')
plt.show()
Step 4 :结果展示
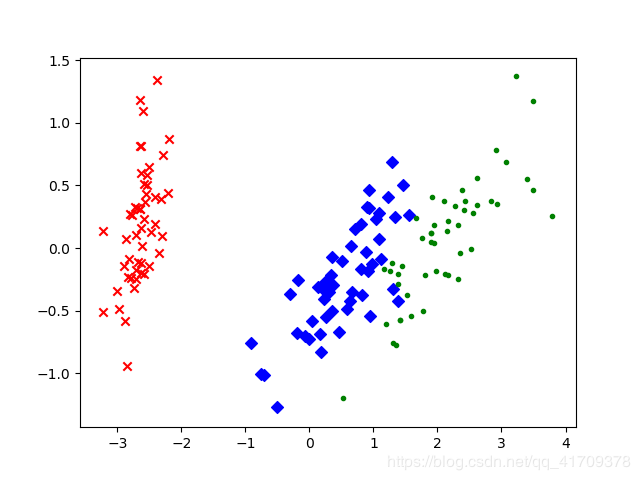
可以看出,降维后的数据仍能够清晰地分成三类。这样不仅能削减数据的维度,降低分类任务的工作量,还能保证分类的质量。
Step 5 :完整程序模块
# -*- coding: utf-8 -*-
# @Time : 2020/3/29 18:55
# @Author : Zudy
# @FileName: course2_1.py
'''
1.用鸢尾花的数据集进行降维处理(PCA)
'''
#加载matplotlib用于数据的可视化
import matplotlib.pyplot as plt
#加载PCA算法包
from sklearn.decomposition import PCA
#加载鸢尾花数据集导入函数
from sklearn.datasets import load_iris
def get_data(reduced_x, y):
'''
1.按照鸢尾花的类别将降维后的数据点保存在不同的列表中
'''
for i in range(len(reduced_x)):
if y[i] == 0:
red_x.append(reduced_x[i][0])
red_y.append(reduced_x[i][1])
elif y[i] == 1:
blue_x.append(reduced_x[i][0])
blue_y.append(reduced_x[i][1])
else:
green_x.append(reduced_x[i][0])
green_y.append(reduced_x[i][1])
if __name__ == '__main__':
#加载数据并进行降维
data = load_iris() #以字典的形式加载鸢尾花数据集
y = data.target #使用y表示数据集中的标签(类别)
x = data.data #使用x表示数据集中的属性数据
pca = PCA(n_components= 2) #设置降维后的主成分数目为2
reduced_x = pca.fit_transform(x) #对原始数据进行降维,并保存在reduced_x中
#按类别对降维后的数据进行保存
red_x, red_y = [], [] #第一类数据点
blue_x, blue_y = [], [] #第二类数据点
green_x, green_y = [], [] #第三类数据点
print(reduced_x)
print(y)
get_data(reduced_x, y)
#对数据点的可视化
fig = plt.figure()
ax = fig.add_subplot()
plt.scatter(red_x, red_y, c='r', marker= 'x')
plt.scatter(blue_x, blue_y, c='b', marker= 'D')
plt.scatter(green_x, green_y, c='g', marker= '.')
plt.show()
作者:三个半_Z