总体与样本（1-2）

1、总体：一个统计问题总有它明确的研究对象，研究对象的全体成为总体（母体）。

2、个体：总体中每个成员称为个体。

然而在统计研究中，人们往往关心每个个体的一项（或几项）数量指标和该数量指标在总体中的分布情况。这是，每个个体具有的数量指标的全体及时总体。

例如：一批灯泡寿命的全体就是总体。 

由于每个个体的出现带有随机性，  即相应的数量指标值的出现带有随机性。从而可把此种数量指标看作随机变量，  我们用一个随机变量或其分布来描述总体。为此常用随机变量的符号或分布的符号来表示总体。
通常，我们用随机变量X，Y,....,等表示总体。当我们说到总体，就是指一个具有确定概率分布的随机变量。

例如：研究某批灯泡的寿命是，我们关心的数量指标就是寿命，那么总体就可以用随机变量X表示，活用其分布函数F（x）表示。

3、有限总体和无限总体

总体中的数目是有限个，则称为有限总体，反之称为无限总体。

4、总体分布

数量指标取不同数值的比率叫做总体分布。

1.样本的定义
为推断总体的分布及各种特征，按一-定的规则从总体中抽取若干个体进行观察试验，以获得有关总体的信息.这一抽取过程称为“抽样”所抽取的部分个体称为样本.通常记为（X1,X2,...Xn）
样本中所包含的个体数目n称为样本容量.
容量为n的样本可以看作n维随机变量.但是，一旦取定一组样本，得到的是n个具体的数(X1,X2,.,Xn,)，称此为样本的一次观察值,简称样本值。
2.简单随机样本
抽取样本的目的是为了利用样本对总体进行统计推断，这就要求样本能很好的反映总体的特性且便于处理.为此，需对抽样提;出一些要求，通常有两条:
（1）代表性: X1,X2..... Xn,中每一一个与所考察的总体x有相同的分布.
（2）独立性: X1,X2..... Xn,是相互独立的随机变量。

满足上述两条性质的样本称为简单随机样本。

获得简单随机样本的抽样方法称为简单随机抽样。
3.样本及样本值
样本
设X是具有分布函数F(x)的随机变量,若X1，X2,,Xn，是具有同一分布函数F(x)、 相互独立的随机变量，则称X1，X2， .,Xn,为从总体X (或总体F(x))中抽取的容量为n的简单随机样本， 简称样本。
样本值
它们的观察值X1,X2,...，Xn称为样本值,又称为X的n个独立的观察值。

4.简单随机抽样的联合分布
获得简单随机样本的抽样方法称为简单随机抽样。
根据定义得:  若X1,X2,...Xn,为F的一个样本，则X1,X2,,Xn,的联合分布函数为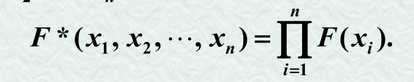

又若X具有概率密度f,
则X1,X2.,Xn，的联合概率密度为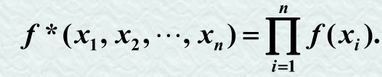

基本概念：个体 总体（有限总体无限总体）随机样本
说明1 一个总体对应一个随机变量X,我们将不区分总体和相应的随机变量，统称为总体X.
说明2  在实际中遇到的总体往往是有限总体，它对应一个离散型随机变量;当总体中包含的个体的个数很大时，在理论上可认为它是-一个无限总体.
总体，样本,样本值的关系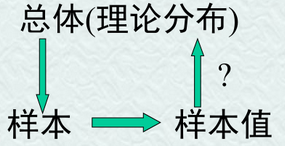

数理统计是从手中已有的资料--样本值，去推断总体的情况--总体的分布F(x)的性质.
样本是联系二者的桥梁.
总体分布决定了样本取值的概率规律，也就是样本取到样本值的规律，因而可以由样本值去推断总体.
 

样本