数学建模插值法——三次埃尔米特插值三次样本插值（笔记）

今天学习了插值法的matlab实现。
我们接触过五种基本的插值方法，有拉格朗日插值、牛顿插值、分段线性插值、分段三次Hermite插值和样条插值（三次）。

插值法在数学建模中的应用：数模比赛中，常常需要根据已知的函数点进行数据、模型的处理和分析，而有时候现有的数据是极少的，不足以支撑分析的进行，这时就需要使用一些数学的方法，“模拟产生”一些新的但又比较靠谱的值来满足需求，这就是插值的作用。

一般来讲，数学建模中主要用到的是 分段三次Hermite插值和三次样条插值
而matlab中都有对应的函数（感慨一下：matlab真强大！）
这两种插值的matlab实现也是本文的重点。

接下来先来用数学定义简单解释一下 分段三次Hermite插值和三次样条插值给有需要的人（便于理解）
1）分段三次Hermite插值
① 埃尔米特插值多项式：插值多项式要求在插值节点上函数值相等，有的实际问题还要求在节点上的导数值相等，甚至高阶导数值也相等，满足这种要求的插值多项式成为埃尔米特插值多项式。
（直接使用埃尔米特插值得到的多项式次数较高，也存在龙格现象，因此在实际应用中，往往使用分段三次埃尔米特插值多项式）
② 分段三次埃尔米特插值：

2）三次样条插值函数

其次，再用matlab分别实现两种插值法
这里应用背景是：MathorCup第六届A题 淡水养殖池塘水华发生及池水净化处理
这道题中，附件2中COD、溶氧、PH值等数据均是隔两周采样一次，数据量不足以用于建立合理的模型，因此要考虑现有数据进行插值以补充数据。具体附件截图如下：

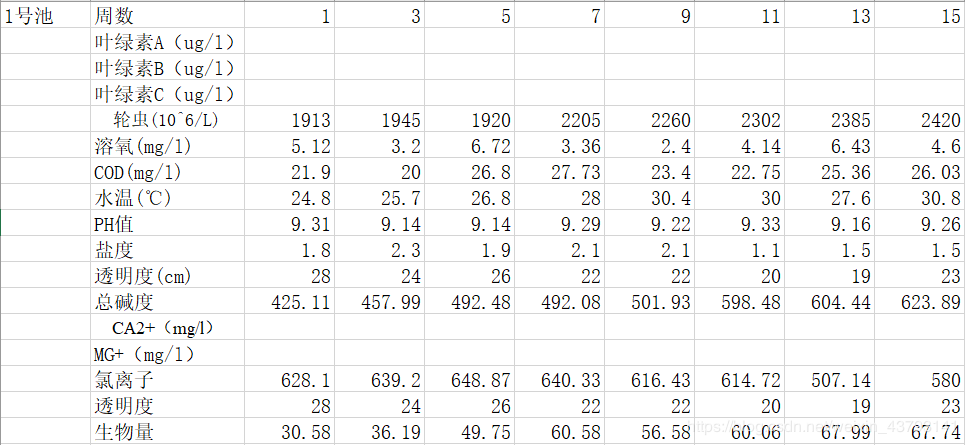
接下来用matlab进行数据补充实现（注：叶绿素A、B、C以及CA2+、MG+等数据不做插值 ）

这是我写的代码：
1、三次埃尔米特插值（spline函数）：
（1）代码部分：

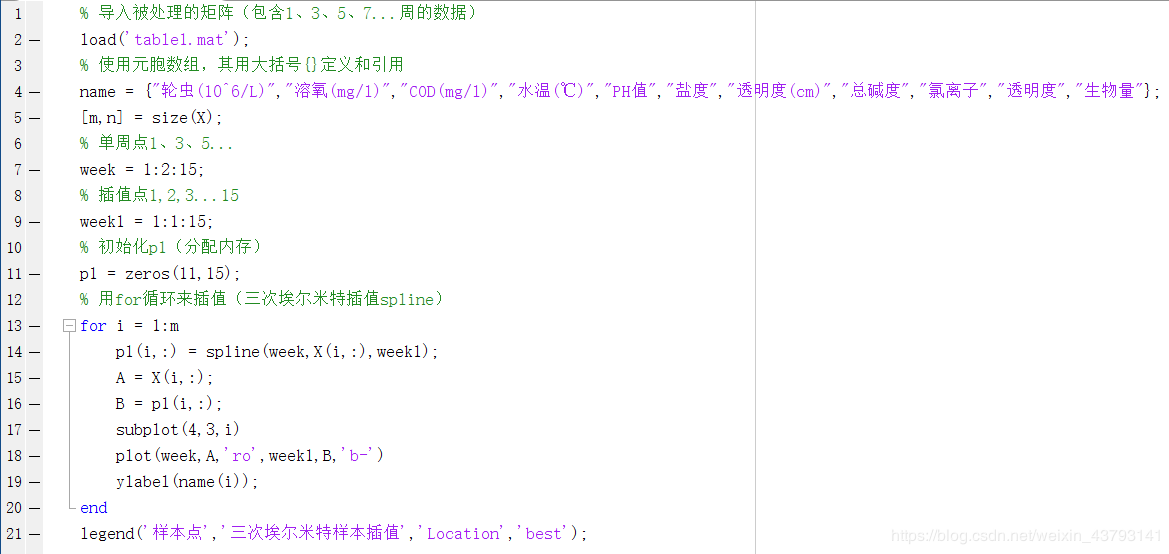
（2）运行结果：

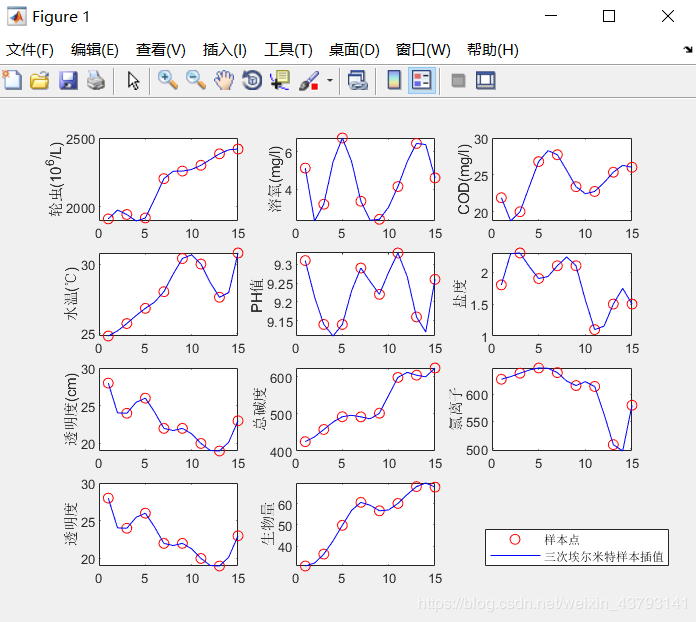
2、三次样条插值
（1）代码部分（pchip函数）：

（2）运行结果：

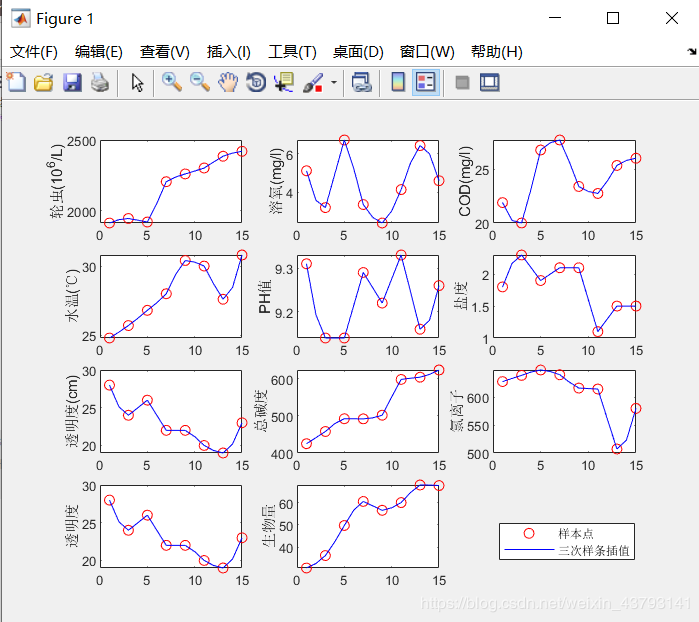
经过两次试验发现，大体上三段埃尔米特插值和三次样条插值插值效果相似，三次样条插值生成的曲线更加平滑。由于我们不知道数据的生成过程，因此这两种插值都可以使用。

注：以上内容均参考清风老师的数学建模视频讲解

埃尔米特 埃尔米特插值 插值法 插值 数学建模 样本 数学