第一章 概率论的基本概念 1.1 随机试验 1.2 样本空间,随机事件
随机试验:
可以在相同的条件下进行重复。 每次试验的可能结果不止一个,并且知道所有可能的结果。 进行一次试验之前不能确定哪一个结果会出现。eg:

实例:

掷出色子点数的6种情况的集合是掷色子这个随机试验的样本空间。每种情况都是一个样本点。
样本空间就是一个全集的概念,我们也可以用Ω\OmegaΩ(大写的Omega)表示
样本点其实也就是他的基本事件,我们用ω\omegaω(小写Omega)表示
练习:


注意 :
同一试验 , 若试验目的不同,则对应的样本空间也不同。
eg:


我们一般用大写的A,B,C来表示事件。
上述试验中,“出现1点”, “出现2点”, … , “出现6点”。都是基本事件。
所有基本事件的集合就是样本空间 ✔
必然事件: 随机试验中必然会出现的结果。上述试验中 “点数不大于6” 就是必然事件。
不可能事件: 随机试验中不可能出现的结果。上述试验中 “点数大于6” 就是不可能事件。
小结:
Ω\OmegaΩ (全集)⟷\longleftrightarrow⟷ 必然事件 ⟷\longleftrightarrow⟷ 样本空间
ϕ\phiϕ ⟷\longleftrightarrow⟷ 不可能事件 ⟷\longleftrightarrow⟷ 空集
事件 ⟷\longleftrightarrow⟷Ω\OmegaΩ 的子集

由之前我们可知:随机事件其实就是一个集合,所以随机事件间的关系及运算其实就是集合的关系和运算。
有以下几种:
包含 等于 并(和事件)
无限可列个:按照某种规律排成一个序列。
eg:
4.交(积事件)
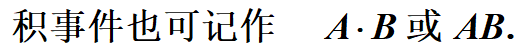
5.差

6.互补相容(互斥)

7.对立


所以对立一定互斥,而互斥不一定对立。
运算规律:

这个我们在离散数学中学过也都很好理解。
例题:


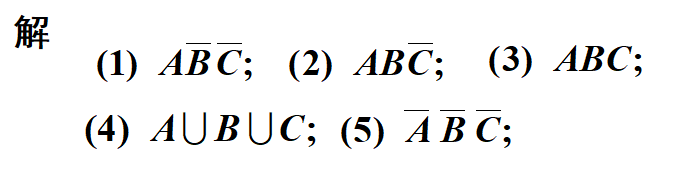

这里简单说一下第七个中的ABC的逆。
不多于两个事件发生 ⟷\longleftrightarrow⟷ 至多两个事件发生 ⟷\longleftrightarrow⟷ (至少三个事件发生)的逆
至少n ⟷\longleftrightarrow⟷ ¬(至多n-1)
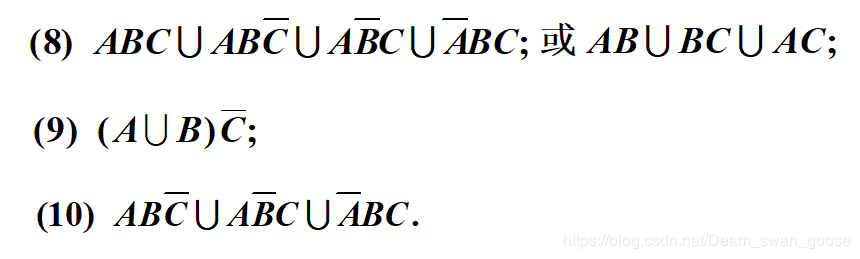
再来:


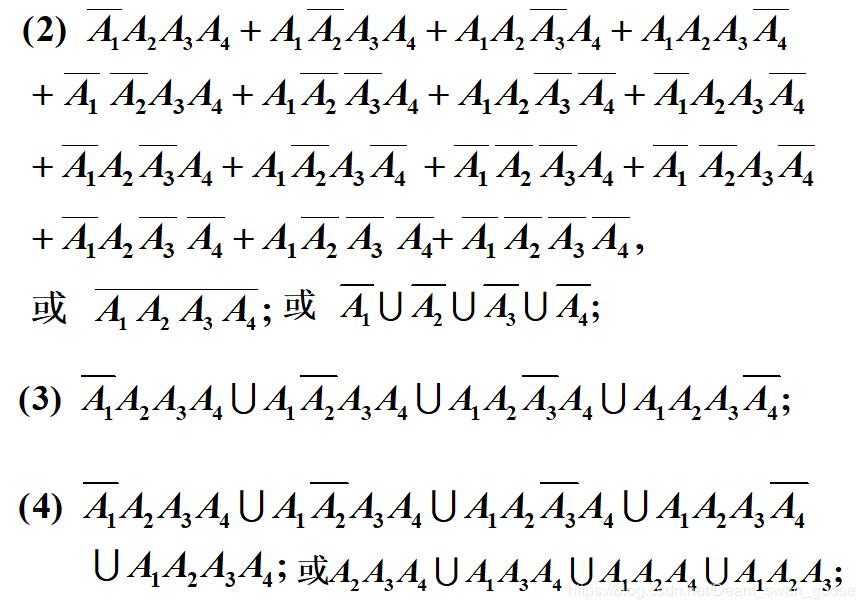
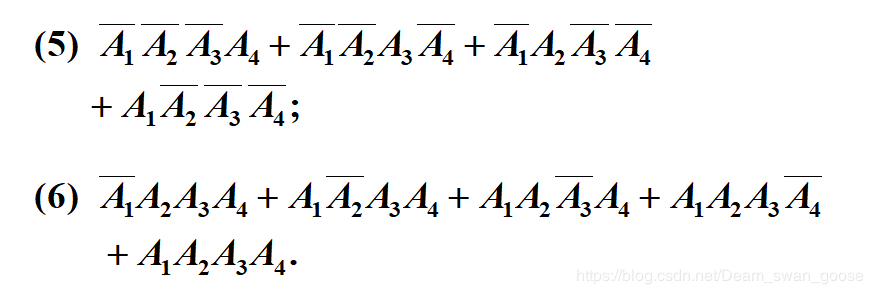
由上道题可见,当A的数量增多的时候麻烦的方法就要写好多了。接下来我给大家分享下解上述题的技巧:
--------------------------------------------技巧--------------------------------------------


“A,B,C中不多于(至多)一个发生” ⟷\longleftrightarrow⟷ “A,B,C中至少有两个不发生”
“A,B,C中不多于(至多)两个发生” ⟷\longleftrightarrow⟷ “A,B,C中至少有一个不发生”
好了,转化成至少以后就按照之前说的就好了。
就至少至多这个点绕一下,其他的都挺简单的。按照这个技巧再把前面的两道例题回炉一下吧。--------------------------------------------技巧--------------------------------------------
概率论与集合论之间的对应关系:

PPT里全集用 SSS来表示,但宋老师和其他慕课里用Ω\OmegaΩ的比较多。

作者:梦里一声何处鸿