极大似然估计（Maximum likelihood estimation，MLE）：用样本估计总体参数

边缘概率、联合概率和条件概率的基本概念。

边缘概率（Marginal Probability）：可以简单理解为单一事件发生的概率。如果A是一个事件，且事件A发生的概率为P(A)P(A)P(A)，则P(A)P(A)P(A)就被称为边缘概率；
联合概率（Joint Probability）：两个或多个事件相交的概率。从视觉上看，它是维恩图上两个事件圆的相交区域。如果A和B是两个事件，那么这两个事件的联合概率记为P(A∩B)P(A∩B)P(A∩B)。
条件概率（Conditional Probability）：条件概率是在已知其他事件已经发生的情况下，某一事件发生的概率。如果A和B是两个事件，那么在B已经发生的前提下，A发生的条件概率写成P(A∣B)P(A|B)P(A∣B)。

P(A∣B)=P(A⋂B)P(B) P(A|B)=\frac{P(A\bigcap B)}{P(B)} P(A∣B)=P(B)P(A⋂B)​

极大似然估计是一种确定模型参数值的方法。参数值的确定使模型所描述的过程产生实际观察到的数据的可能性最大化。这听起来有点绕，我们可以通过下图中这个最简单的例子来理解：

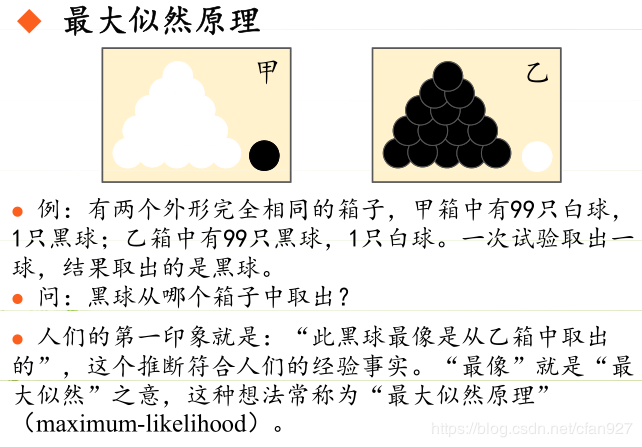
下面用一个稍微复杂一些的例子来解释这个概念。假设我们从某个过程中观察到10个数据点（例如，每个数据点可以表示学生回答一个特定考试问题所需的时间/秒）。这10个数据点如下图所示：

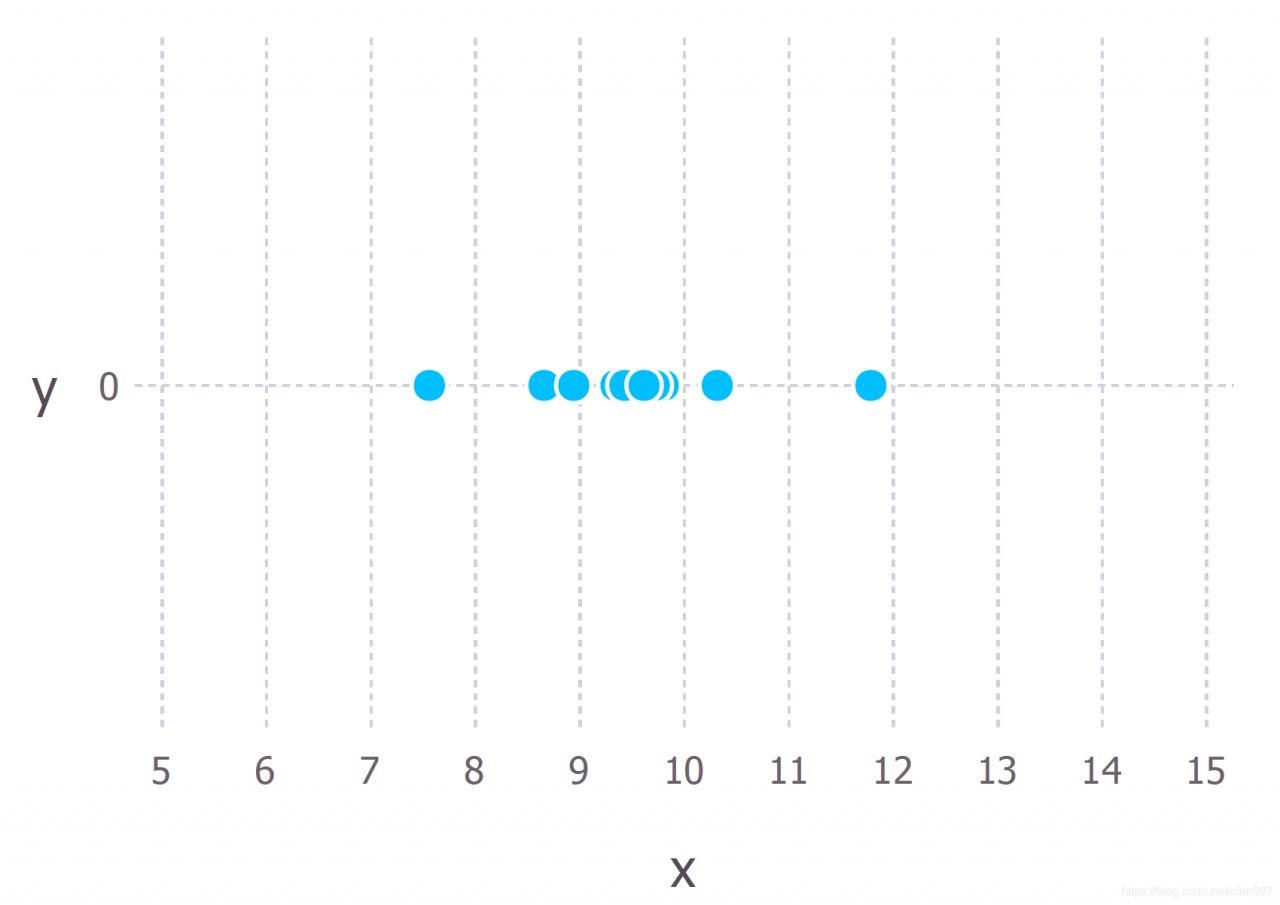
我们首先必须确定生成这些数据的模型，有了模型才能去估计模型的参数，这很重要。但模型的确定通常来自于一些领域的专业知识，我们不会在这里讨论。

对于上述这些数据，我们假设数据生成过程可以用高斯（正态）分布来充分描述。（10个数据点显然不足以判定这些数据的分布，这里只做一个示例）。

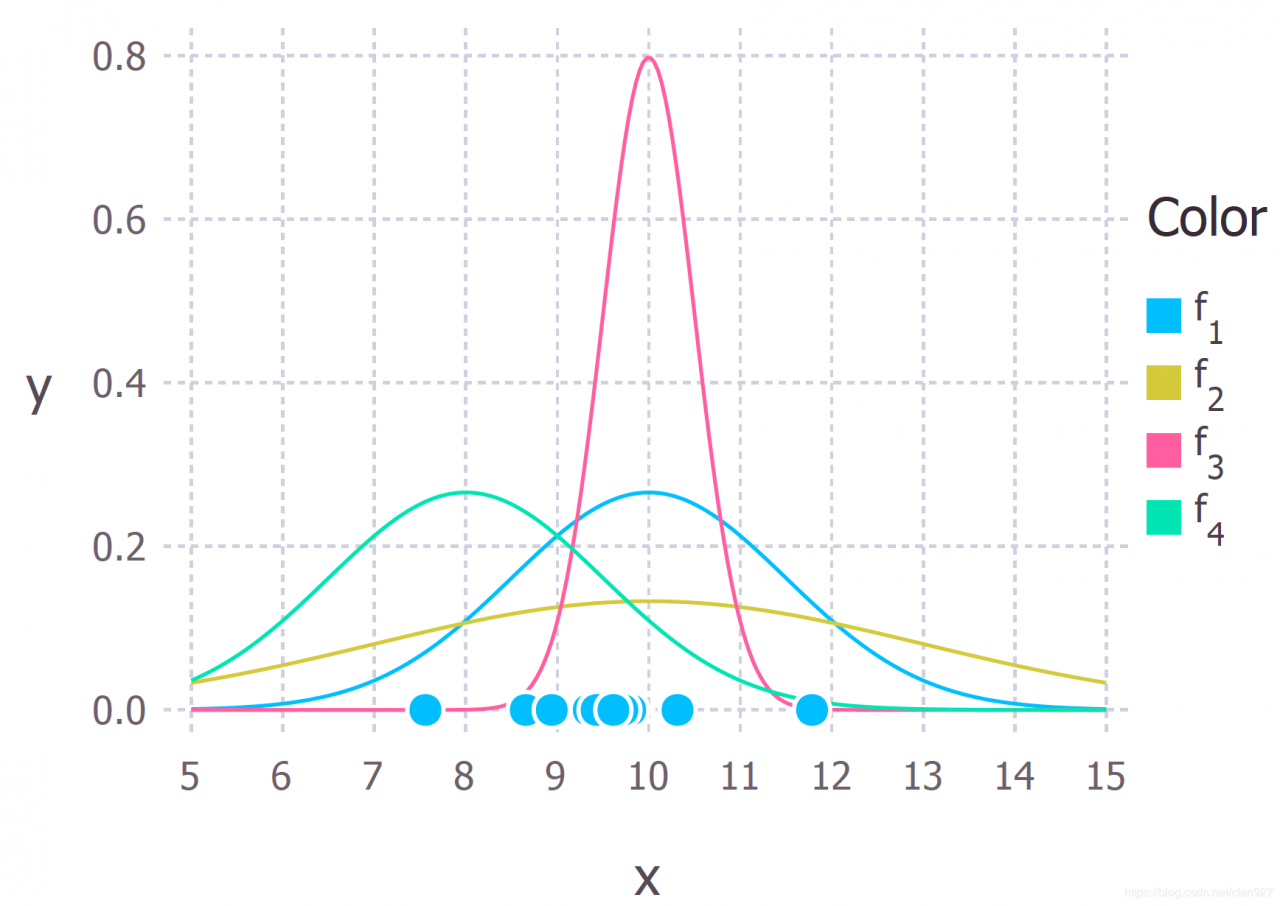
高斯分布有两个参数：均值μ\muμ和标准差σ\sigmaσ。这些参数值的不同会产生不同的曲线。我们想知道哪条曲线最有可能产生我们观察到的数据点（见上图）。通过最大似然估计法，我们会得到一个使数据和曲线最吻合的μ\muμ、σ\sigmaσ值。（生成数据的真实分布为f1∼N(10,2.25)f1 \sim N(10,2.25)f1∼N(10,2.25)，即上图中的蓝色曲线。）。

现在我们已经对极大似然估计有了一个直观的理解，下面继续学习如何计算参数值。我们将找到的参数值称为极大似然估计（MLE）。

为了方便计算过程的展示和便于理解，我们假设有3个数据点{9,9.5,11}\{9,9.5,11\}{9,9.5,11}，它们是由一个符合高斯分布的过程产生的且相互之间是独立的（排除条件概率，便于理解）。接下来看如何通过极大似然估计来计算该高斯分布的参数值μ\muμ和σ\sigmaσ。

由高斯分布产生的单个数据点xxx的观测概率密度为：

P(x;μ,σ)=1σ2πexp⁡(−(x−μ)22σ2) P(x;\mu,\sigma)=\frac{1}{\sigma \sqrt{2\pi}}\exp(-\frac{(x-\mu)^2}{2\sigma^2}) P(x;μ,σ)=σ2π​1​exp(−2σ2(x−μ)2​)

则观测三个数据点的联合概率密度为：

P(9,9.5,11;μ,σ)=1σ2πexp⁡(−(9−μ)22σ2)×1σ2πexp⁡(−(9.5−μ)22σ2)×1σ2πexp⁡(−(11−μ)22σ2) P(9,9.5,11;\mu,\sigma)= \frac{1}{\sigma \sqrt{2\pi}}\exp(-\frac{(9-\mu)^2}{2\sigma^2}) \times \frac{1}{\sigma \sqrt{2\pi}}\exp(-\frac{(9.5-\mu)^2}{2\sigma^2}) \times \frac{1}{\sigma \sqrt{2\pi}}\exp(-\frac{(11-\mu)^2}{2\sigma^2}) P(9,9.5,11;μ,σ)=σ2π​1​exp(−2σ2(9−μ)2​)×σ2π​1​exp(−2σ2(9.5−μ)2​)×σ2π​1​exp(−2σ2(11−μ)2​)

现在的目标就是找到一组μ,σ\mu,\sigmaμ,σ值，使得上面的值最大。上面的公式可以看成一个二元函数，求使其取最大值的参数可以使用求导的方式。

然而上面的公式直接求导比较困难，所以通过对表达式取自然对数来简化它（对数似然函数，log likelihood）。因为自然对数是一个单调递增的函数，所以它确保了取对数后概率的最大值与原概率函数在同一点上。因此，我们可以用更简单的对数似然函数代替原始似然函数。

对原表达式取对数得到：

ln(P(x;μ,σ))=ln(1σ2σ2)−(9−μ)22σ2+ln(1σ2σ2)−(9.5−μ)22σ2+ln(1σ2σ2)−(11−μ)22σ2=−3ln(σ)−32ln(2π)−12σ2[(9−μ)2+(9.5−μ)2+(11−μ)2] \begin{aligned} ln(P(x;\mu,\sigma)) &= ln(\frac{1}{\sigma\sqrt{2\sigma^2}})-\frac{(9-\mu)^2}{2\sigma^2} + ln(\frac{1}{\sigma\sqrt{2\sigma^2}})-\frac{(9.5-\mu)^2}{2\sigma^2} + ln(\frac{1}{\sigma\sqrt{2\sigma^2}})-\frac{(11-\mu)^2}{2\sigma^2} \\ &= -3ln(\sigma)-\frac{3}{2}ln(2\pi)-\frac{1}{2\sigma^2}[(9-\mu)^2+(9.5-\mu)^2+(11-\mu)^2] \end{aligned} ln(P(x;μ,σ))​=ln(σ2σ2​1​)−2σ2(9−μ)2​+ln(σ2σ2​1​)−2σ2(9.5−μ)2​+ln(σ2σ2​1​)−2σ2(11−μ)2​=−3ln(σ)−23​ln(2π)−2σ21​[(9−μ)2+(9.5−μ)2+(11−μ)2]​

对μ\muμ求偏导，有：

∂ln(P(x;μ,σ))∂μ=1σ2[9+9.5+11−3μ] \frac{\partial ln(P(x;\mu,\sigma))}{\partial \mu}=\frac{1}{\sigma^2}[9+9.5+11-3\mu] ∂μ∂ln(P(x;μ,σ))​=σ21​[9+9.5+11−3μ]

令等式左边为零，即可得到μ\muμ的估计值：

μ=9+9.5+113=9.833 \mu=\frac{9+9.5+11}{3}=9.833 μ=39+9.5+11​=9.833

同样的，对σ\sigmaσ求偏导即可得到它的估计值，这里不再赘述。

求解最大似然估计量的一般步骤：
（1）写出似然函数；
（2）对似然函数取对数，并整理；
（3）求导数；
（4）解似然方程。

但要注意的是，由于对数似然函数的导数的复杂性，极大似然估计并不是在所有情形下都能够得到问题的解。因此，可以使用期望最大化算法等迭代方法来寻找参数估计的数值解。不过总体思路还是一样的。

[1] https://towardsdatascience.com/probability-concepts-explained-maximum-likelihood-estimation-c7b4342fdbb1

样本 极大似然估计 参数