统计学之离散指标（全距、内距、异众比率、平均差与标准差）

离散指标
含义：反映数值差异程度的指标，亦称变异指标。
作用：衡量平均水平的代表性，反映均衡性和稳定性，为统计推断提高依据。

1.全距
全距（Range）或极差
R＝最大值 - 最小值=Max-Min
优点：简单明了
缺点：只反映变动幅度，最易受极端值影响

2.四分位差
四分位差也称为内距
Qd ＝ QU－ QL

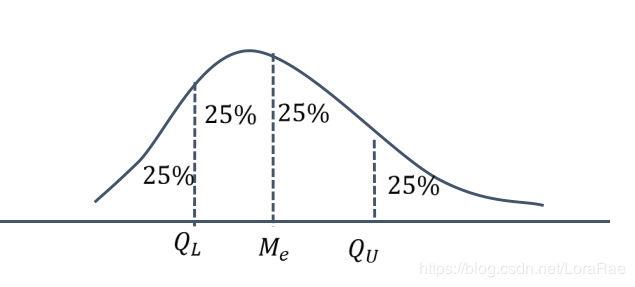
特点：中间50%个体的变动幅度，不受极值影响。

3.异众比率
非众数组频数占总频数之比
反映众数的代表性

4.平均差
即平均绝对偏差（Mean Absolute Deviation）
在资料未分组的情况下，计算公式:

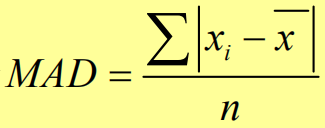
在资料已分组的情况下，计算公式:

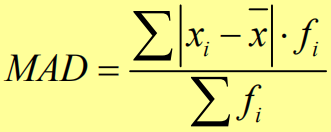
平均差特点
（1）反映全部标志值变动
（2）受水平高低、计量单位影响

5.方差标准差
方差即离差平方的算术平均数，标准差是方差的算术平方根。

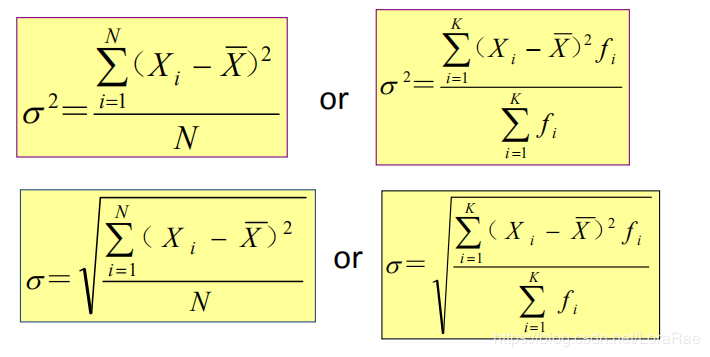
样本方差和样本标准差（分母为n-1）
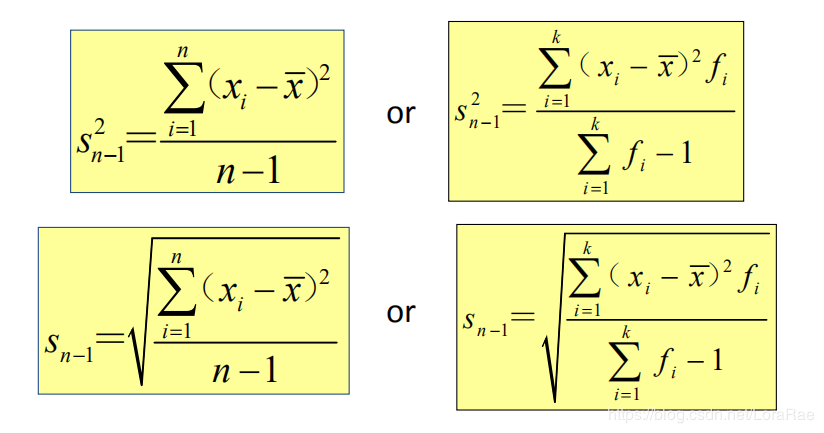简便公式：
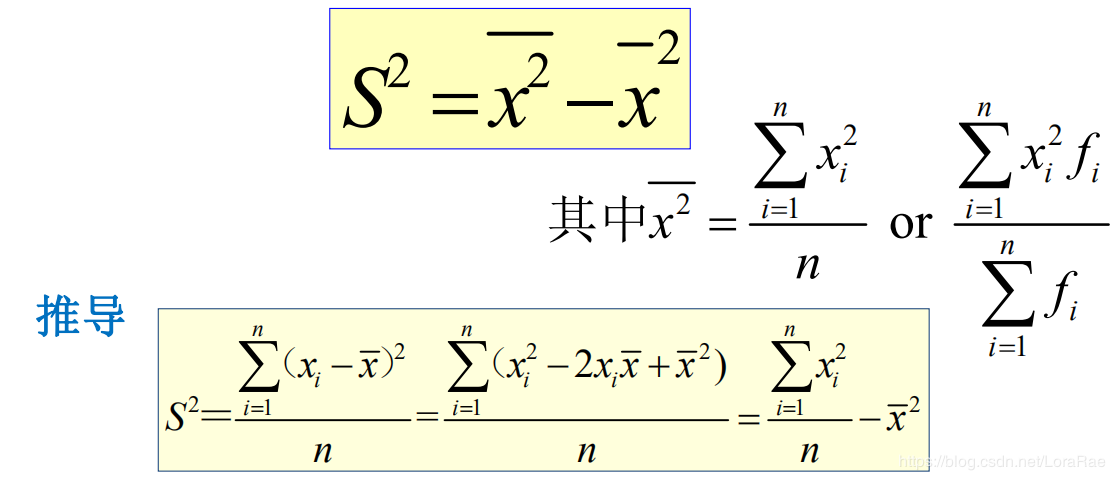性质：

优点：
反应灵敏、适合代数计算、能够用在统计推断内
缺点：
受量纲约束、受水平影响

统计学