统计学中基础概念说明
1、什么是描述性统计?
2、统计量
1)常用统计量
2)变量的类型
3)本文章使用的相关python库
3、频率与频数
1)频率与频数的概念
2)代码演示:计算鸢尾花数据集中每个类别的频数和频率
4、集中趋势
1)均值、中位数、众数概念
2)均值、中位数、众数三者的区别
3)不同分布下,均值、中位数、众数三者之间的关系
4)代码:计算鸢尾花数据集中花萼长度的均值、中位数、众数
5、集中趋势:分位数
1)分位数的概念
2)怎么求分位数?
3)分位数是数组中的元素的情况
4)分位数不是数组中的元素的情况:使用分摊法求分位数
5)numpy中计算分位数的函数:quantile()
6)pandas中计算分位数的函数:describe()
6、离散程度
1)极差、方差、标准差的概念
2)极差、方差、标准差的作用
3)代码:计算鸢尾花数据集中花萼长度的极差、方差、标准差
7、分布形状:偏度和峰度
1)偏度
2)峰度
描述性统计,就是从总体数据中提取变量的主要信息(总和、均值等),从而从总体层面上,对数据进行统计性描述。在统计的过程中,通常会配合绘制相关的统计图来进行辅助。
2、统计量描述性统计所提取的含有总体性值的信息,我们称为统计量。
1)常用统计量* 频数与频率
+ 预数
+ 频率
* 集中趋势分析
+ 均值
+ 中位数
+ 众数
+ 分位数
* 离散程度分析
+ 极差
+ 方差
+ 标准差
* 分布形状
+ 偏度
+ 峰度
2)变量的类型
* 类别变量
+ 无序类别变量
+ 有序类别变量
* 数值变量
+ 连续变量
+ 离散型变量
3)本文章使用的相关python库
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
from sklearn.datasets import load_iris
from scipy import stats
sns.set(style="darkgrid")
mpl.rcParams["font.family"] = "SimHei"
mpl.rcParams["axes.unicode_minus"] = False
warnings.filterwarnings("ignore")
3、频率与频数
1)频率与频数的概念
数据的频数与频率适用于类别变量。
频数:指一组数据中类别变量的每个不同取值出现的次数。
频率:指每个类别变量的频数与总次数的比值,通常采用百分数表示。
2)代码:计算鸢尾花数据集中每个类别的频数和频率
iris = load_iris()
# iris是一个类字典格式的数据,data、target、feature_names、target_names都是键
display(iris.data[:5],iris.target[:5])
# feature_names是每一列数据的特征名。target_names是鸢尾花的属种名
display(iris.feature_names,iris.target_names)
# reshape(-1,1)表示将原始数组变为1列,但是行数这里我写一个-1,表示系统
# 会根据我指定的列数,自动去计算出行数。reshape(1,-1)含义同理
dt = np.concatenate([iris.data,iris.target.reshape(-1,1)],axis=1)
df = pd.DataFrame(dt,columns=iris.feature_names + ["types"])
display(df.sample(5))
# 计算鸢尾花数据集中每个类别出现的频数
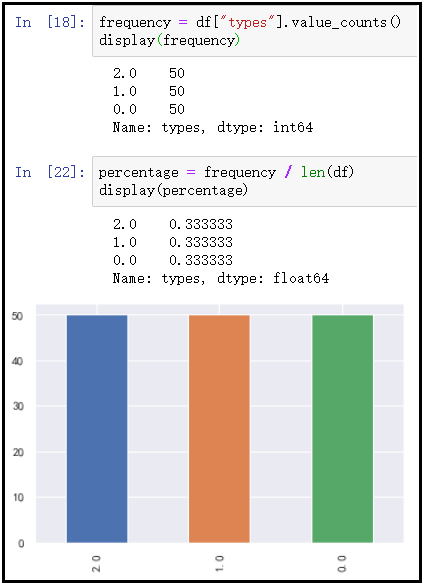
frequency = df["types"].value_counts()
display(frequency)
percentage = frequency / len(df)
display(percentage)
frequency.plot(kind="bar")
结果如下:
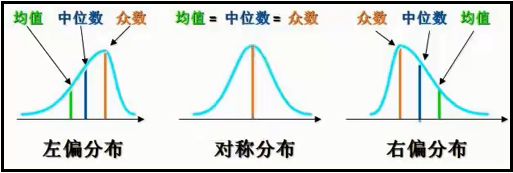
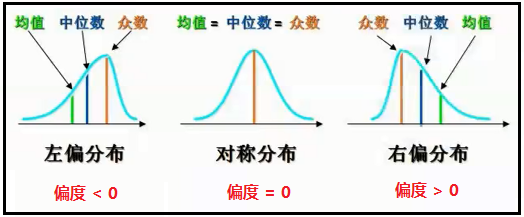
记忆方法:哪边的尾巴长,就叫做 “X偏”。左边的尾巴长,就叫做“左偏”;右边的尾巴长,就叫做“右偏”。并且均值离着尾巴最近,中位数总是在最中间,众数离着尾巴最远。
mean = df["sepal length (cm)"].mean()
display(mean)
median = df["sepal length (cm)"].median()
display(median)
# 由于series中没有专门计算众数的函数,因此需要我们统计频数最大的那些值
s = df["sepal length (cm)"].value_counts()
s = s[s.values == s.values[0]]
s.index.tolist()
t = s.index[0]
t
# scipy的stats模块中,可以计算众数
from scipy import stats
t = stats.mode(df["sepal length (cm)"])
# 注意:t展示的类字典格式的数据类型,mode展示众数,count用于展示众数出现的次数
display(t.mode,t.count)
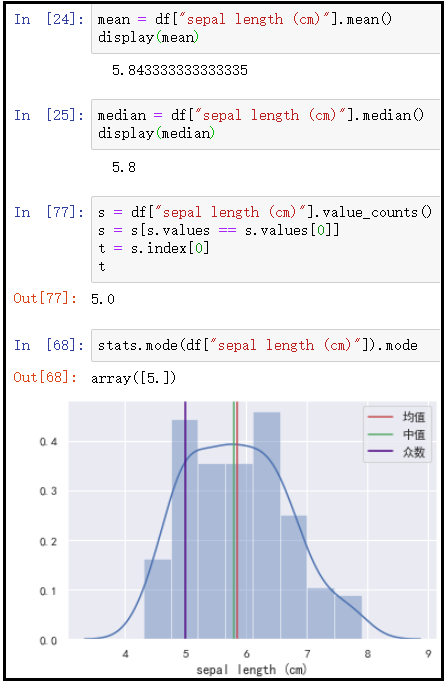
sns.distplot(df["sepal length (cm)"])
plt.axvline(mean,ls="-",color="r",label="均值")
plt.axvline(median,ls="-",color="g",label="中值")
plt.axvline(t,ls="-",color="indigo",label="众数")
plt.legend(loc="best")
结果如下:
 2)怎么求分位数
2)怎么求分位数
给定一组数据(存放在数组中),我们要如何计算其四分位值呢?首先要明确一点,四分位值未必一定等同于数组中的某个元素。
在Python中,四分位值的计算方式如下:
① 首先计算四分位的位置。
q1_index=1+(n-1)*0.25
q2_index=1+(n-1)*0.5
q3_index=1+(n-l)*0.75
其中,位置index从1开始,n为数组中元素的个数。
② 根据位置计算四分位值。
如果index为整数(小数点后为0),四分位的值就是数组中索引为index的元素(注意位置索引从1开始)。
如果index不是整数,则四分位位置介于ceil(index)与floor(index)之间,根据这两个位置的元素确定四分位值。
x = np.arange(10,19)
n = len(x)
# 计算每个分位数的位置,这个位置是从1开始的。但是数组元素索引从0开始的
q1_index=1+(n-1)*0.25
q2_index=1+(n-1)*0.5
q3_index=1+(n-1)*0.75
# 这里计算出来的数字是浮点类型,需要转化为小数,才能当作索引
q1_index,q2_index,q3_index
# 计算分位数
index = np.array([q1_index,q2_index,q3_index]).astype(np.int32)
index -= 1
q = x[index]
q
结果如下:

绘制图形:
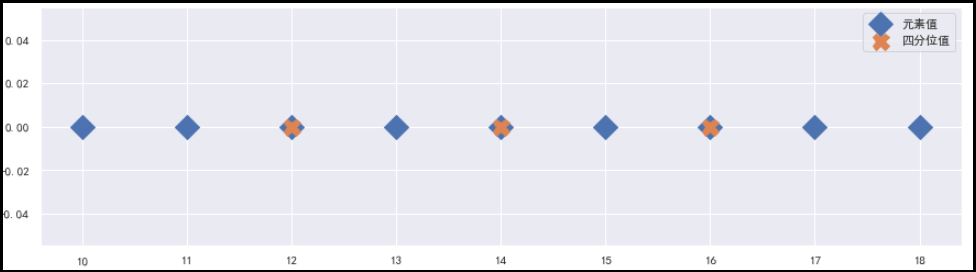
plt.figure(figsize=(15,4))
plt.xticks(x)
plt.plot(x,np.zeros(len(x)),ls="",marker="D",ms=15,label="元素值")
plt.plot(x[index],np.zeros(len(index)),ls="",marker="X",ms=15,label="四分位值")
plt.legend()
结果如下:
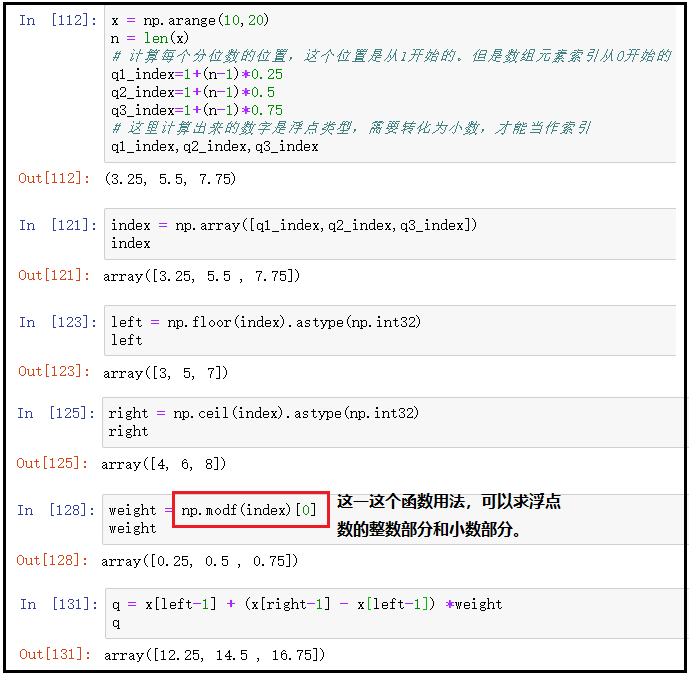
x = np.arange(10,20)
n = len(x)
# 计算每个分位数的位置,这个位置是从1开始的。但是数组元素索引从0开始的
q1_index=1+(n-1)*0.25
q2_index=1+(n-1)*0.5
q3_index=1+(n-1)*0.75
q1_index,q2_index,q3_index
# 计算分位数
index = np.array([q1_index,q2_index,q3_index])
index
left = np.floor(index).astype(np.int32)
left
right = np.ceil(index).astype(np.int32)
right
weight = np.modf(index)[0]
weight
q = x[left] + (x[right] - x[left]) *weight
q
结果如下:
绘制图形:
plt.figure(figsize=(15,4))
plt.xticks(x)
plt.plot(x,np.zeros(len(x)),ls="",marker="D",ms=15,label="元素值")
plt.plot(q,np.zeros(len(q)),ls="",marker="X",ms=15,label="四分位值")
plt.legend()
for v in q:
plt.text(v,0.01,v,fontsize=15)
plt.legend()
结果如下:

x = np.arange(10,19)
np.quantile(x,[0.25,0.5,0.75])
x = np.arange(10,20)
np.quantile(x,[0.25,0.5,0.75])
结果如下:

从结果中可以看到:上述我们自己计算的分位数结果,和使用该函数计算的分位数的结果,是一样的。
x = pd.Series(np.arange(10,19))
x.describe()
x = pd.Series(np.arange(10,20))
x.describe()
结果如下:
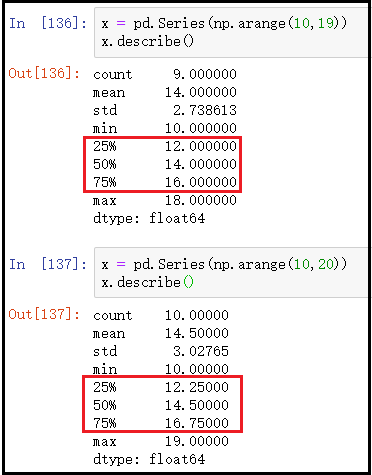
注意:describe()中可以传入percentiles参数,获取指定分位数的值。
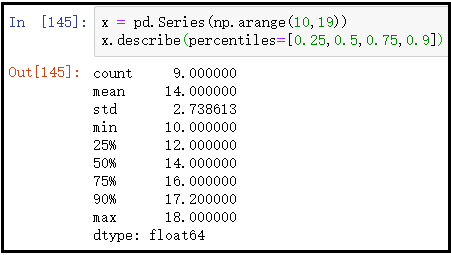
x = pd.Series(np.arange(10,19))
x.describe(percentiles=[0.25,0.5,0.75,0.9])
结果如下:

iris = load_iris()
dt = np.concatenate([iris.data,iris.target.reshape(-1,1)],axis=1)
df = pd.DataFrame(dt,columns=iris.feature_names + ["types"])
display(df.sample(5))
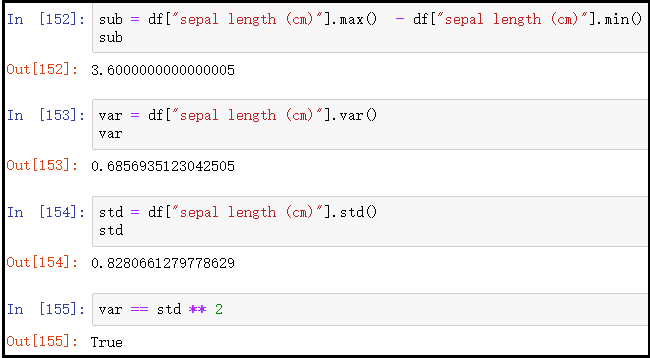
sub = df["sepal length (cm)"].max() - df["sepal length (cm)"].min()
sub
var = df["sepal length (cm)"].var()
var
std = df["sepal length (cm)"].std()
std
var == std ** 2
结果如下:
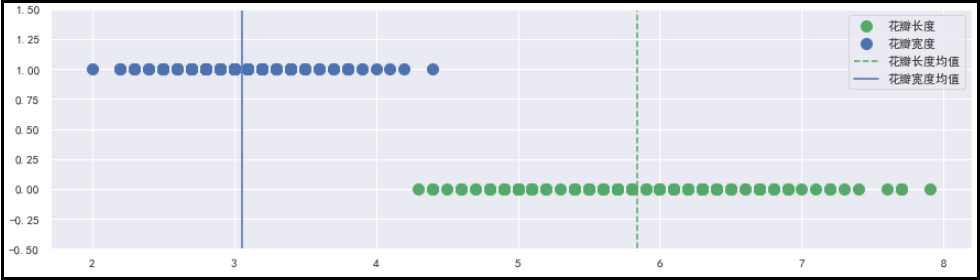
绘制图形:
plt.figure(figsize=(15,4))
plt.ylim(-0.5,1.5)
plt.plot(df["sepal length (cm)"],np.zeros(len(df)),ls="",marker="o",ms=10,color="g",label="花瓣长度")
plt.plot(df["sepal width (cm)"],np.ones(len(df)),ls="",marker="o",ms=10,color="b",label="花瓣宽度")
plt.axvline(df["sepal length (cm)"].mean(),ls="--",color="g",label="花瓣长度均值")
plt.axvline(df["sepal width (cm)"].mean(),ls="-",color="b",label="花瓣宽度均值")
plt.legend()
结果如下:
 ② 代码如下
② 代码如下
t1 = np.random.randint(1,11,100)
t2 = np.random.randint(11,21,500)
t3 = np.concatenate([t1,t2])
left_skew = pd.Series(t3)
t1 = np.random.randint(1,11,500)
t2 = np.random.randint(11,21,100)
t3 = np.concatenate([t1,t2])
right_skew = pd.Series(t3)
display(left_skew.skew(),right_skew.skew())
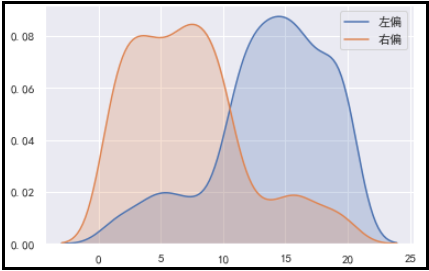
sns.kdeplot(left_skew,shade=True,label="左偏")
sns.kdeplot(right_skew,shade=True,label="右偏")
plt.legend()
结果如下:
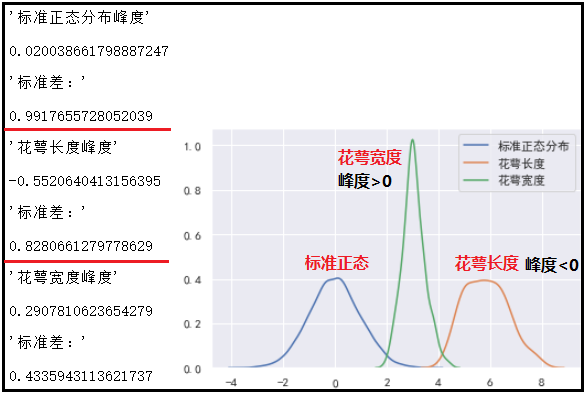
standard_normal = pd.Series(np.random.normal(0,1,10000))
display("标准正态分布峰度",standard_normal.kurt(),"标准差:",standard_normal.std())
display("花萼长度峰度",df["sepal length (cm)"].kurt(),"标准差:",df["sepal length (cm)"].std())
display("花萼宽度峰度",df["sepal width (cm)"].kurt(),"标准差:",df["sepal width (cm)"].std())
sns.kdeplot(standard_normal,label="标准正态分布")
sns.kdeplot(df["sepal length (cm)"],label="花萼长度")
sns.kdeplot(df["sepal width (cm)"],label="花萼宽度")
结果如下:
作者:Huang supreme