《统计学习方法》——第一章 统计学习方法概论
1.1 统计学习
统计学习就是计算机系统通过运用数据及统计方法提高系统性能得机器学习。现在人们提及得机器学习,往往是指统计机器学习。 统计学习由监督学习、非监督学习、半监督学习和强化学习等组成。
李航的《统计学习方法》以介绍统计学习方法为主,其中第2-8 章都是监督学习方法为主。
1.2 监督学习
输入/输出空间:监督学习中,输入与输出的所有可能取值的集合分别称为输入空间和输出空间。输入与输出空间可以是有限元素的集合,也可以是整个欧式空间,通常,输出空间远远小于输入空间。
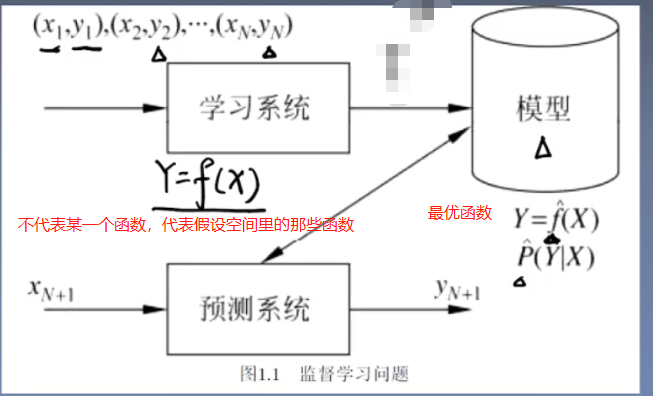
例如 训练集为T ={(h1,y1),(x2,y2), ... ,(xn,yn)},该训练集有n个样本点,每个样本点由两部分组成,一个是x,一个是y;每个样本点称为实例,其中x为输入变量,y为输出变量。x可以为一个数或一个向量。
若x为一个小n维的向量, ![]() ,x属于输入空间,输出空间是每一个y属于的空间。
,x属于输入空间,输出空间是每一个y属于的空间。
特征空间:每个具体的输入是一个实例,通常由特征向量表示(上述x就是一个n维的特征向量)。所有的特征向量存在的空间称为特征空间。
一般情况下,输入空间和特征空间是一样的,但特殊情况下不同。比如,我们拿到的数据为x,但我们不想只用x,想用x、x的平方,x的三次方等,那么从x扩张的三维空间就是特征空间,原来的空间是一个一维空间。联合概率分布: 比如说我们有一个模型,有输入变量空间X=(x1,x2,...,xn) 和输出变量空间Y=(y1,y2,...,ym),可能是离散的,可能是连续的。那么现在我们这个模型的作用就是在输入一个x的时候,能够给出一个y,也可以说我们这个模型的作用就是找到X和Y的联合概率分布P(X,Y)。那么我们就可以根据其联合概率得到条件概率,就可以得到 P(Y∣X),于是就可以利用这个条件概率找到给定一个x的情况下,最大可能的y是哪一个。(原文链接:https://blog.csdn.net/qq_39636214/article/details/85036837)
假设空间: 假设空间中就是一个个备选模型,然后从备选模型中选一个最优模型。模型形式分为决策函数Y=f(x) 和条件概率分布P(y|x)。
1.3 统计学习三要素
1.3.1 模型
 ,
,![]() 指的是函数的参数。
指的是函数的参数。
1.3.2 策略
以某个标准说明该模型是最优模型,策略体现在损失函数上,损失函数是对每个实例,我们的预测的和真实值之间差别的惩罚。
0-1 损失函数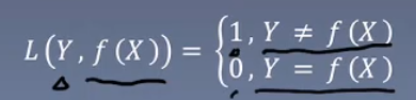 该损失函数用于分类问题中;若观测值和真实值相同,则把损失视为0。反之为1。
平方损失函数
该损失函数用于分类问题中;若观测值和真实值相同,则把损失视为0。反之为1。
平方损失函数 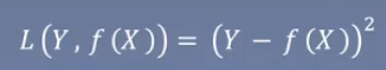 该损失函数与绝对损失函数相比,对差值比较大的实例更敏感,一般用于回归问题中(x,y为连续的值)。
绝对损失函数
该损失函数与绝对损失函数相比,对差值比较大的实例更敏感,一般用于回归问题中(x,y为连续的值)。
绝对损失函数 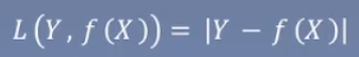 和平方损失函数类似。
对数损失函数或对数似然损失函数
和平方损失函数类似。
对数损失函数或对数似然损失函数 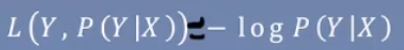 ,前三个都属于决策模型,该损失函数属于条件概率模型,在决策模型中当预测值和真实值相同时,损失为0。但是在条件概率模型中,损失不可能为0。在该模型中我们给的是Y在X下的一个条件概率分布,该分布和观测值之间的损失度量就是通过一个函数实现的。
,前三个都属于决策模型,该损失函数属于条件概率模型,在决策模型中当预测值和真实值相同时,损失为0。但是在条件概率模型中,损失不可能为0。在该模型中我们给的是Y在X下的一个条件概率分布,该分布和观测值之间的损失度量就是通过一个函数实现的。
以上的损失函数是对一个具体实例进行处理,在实际情况中,一个完整的数据集包含多个实例,为整合多个实例生成的损失值,我们提出策略这一概念。
经验风险最小化(ERM),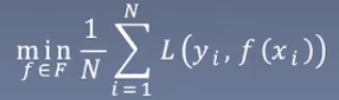 假设每个假设空间中的f,在每个实例中都有一个损失
假设每个假设空间中的f,在每个实例中都有一个损失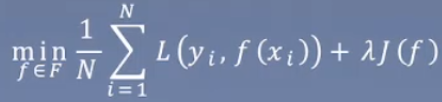 ,与ERM相比加入正则项
,与ERM相比加入正则项1.3.3 算法
算法是怎样根据策略从假设空间中选取最优模型
1.4 模型评估和模型选择
1.4.1训练误差和测试误差
统计学习的目的不仅要在训练集上取得较好效果,而是也要对未知数据有很好的预测能力。当损失函数给定后,基于损失函数的模型的训练误差和模型的测试误差成了学习方法的评估标准。
训练误差: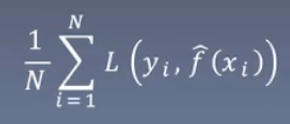 ,测试误差:
,测试误差: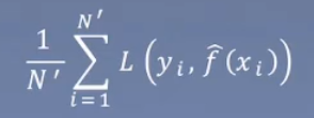 。
。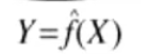 为学习到的模型,训练误差就是在训练集中,该模型下的平均损失。测试误差就是在测试集中,该模型下的平均损失。
为学习到的模型,训练误差就是在训练集中,该模型下的平均损失。测试误差就是在测试集中,该模型下的平均损失。
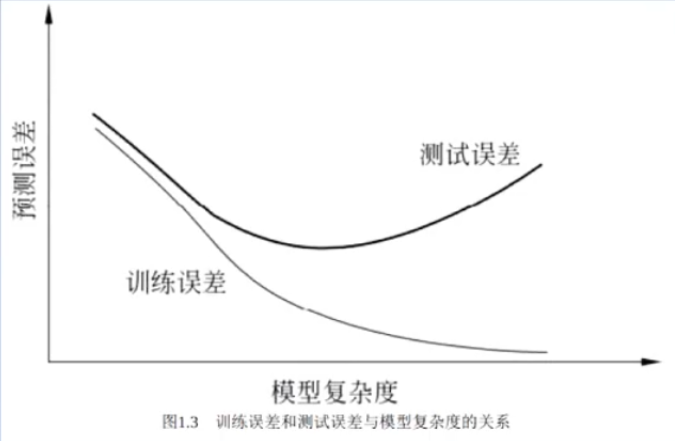
1.4.2 过拟合与模型选择
过拟合:一昧的追求对训练数据的拟合程度,导致所选择的模型的复杂度比真实模型的复杂度更高。
模型选择中不仅要考虑对已知数据的预测能力,也要考虑对未知数据的预测能力。
1.5 正则化与交叉验证(模型选择的两个方法)
1.6 泛化能力
泛化误差:如果学得到的模型是![]() ,那么用这个模型对未知数据预测的误差即为泛化误差。
,那么用这个模型对未知数据预测的误差即为泛化误差。 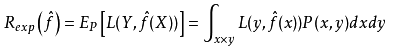
泛化误差上界:对于二分类问题,当假设空间是有限个函数的集合F = {f1,f2,...,fd}时,对任意一个函数f属于F,至少以概率![]() ,以下不等式成立:
,以下不等式成立:
备选模型f在训练集上的经验风险加一项可以控制住在测试集中得期望风险。
1.7 生成模型和判别模型
把统计学习方法根据模型的类别分为生成模型和判别模型。由P(x,y)生成p(y|x),给定了输入X产生输出Y的生成关系,叫做生成生成方法;判别方法是由f(x)或者条件概率分布P(Y|X)作为预测的模型,给定输入X,应该预测出什么样的输出Y(直接学习f(x)或者条件概率分布P(Y|X))。
1.8 分类问题 (二分类问题)
分类器:监督学习从数据中学习一个分类模型或分类决策函数。(就是个模型),可能的输出叫做类。
TP——将正类预测为正类
FP——将负类预测为正类
FN——将正类预测为负类
TN——将负类预测为负类
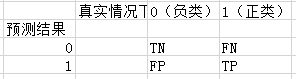
精确率: 真实情况下是正类的这些在预测出是正类中的占比
真实情况下是正类的这些在预测出是正类中的占比
召回率: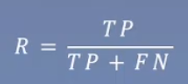 真实情况下是正类的这些在真实情况中的占比,表现预测正确的概率是多少
真实情况下是正类的这些在真实情况中的占比,表现预测正确的概率是多少
1.9 标注问题和1.10回归问题就不多提啦~~
作者:Lyons_boy