小白谈计算机图形学(二)如何画圆及拓展
与直线不同,圆上每点的斜率都是变化的,这一讲我们来介绍圆的画法,首先注意到圆具有八对称性,即只需研究18\frac{1}{8}81圆周即可。
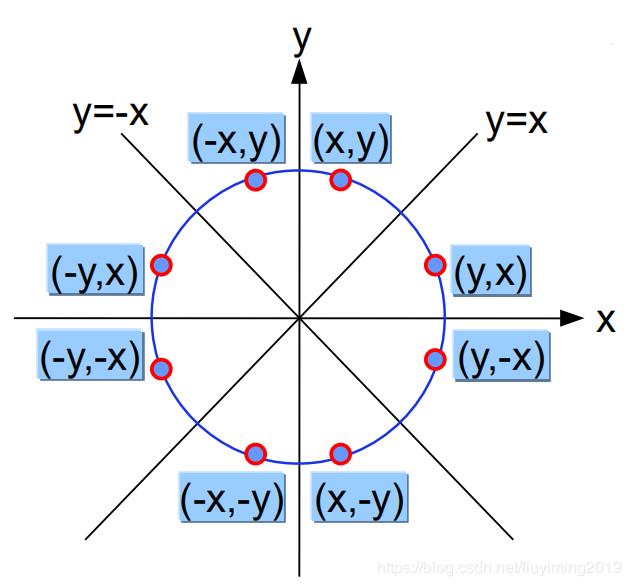
{x=rcosθy=rsinθ \left\{ \begin {aligned} x = r\cos\theta\\ y=r\sin\theta\\ \end {aligned} \right. {x=rcosθy=rsinθ
高效的画圆法必须避免三角函数计算和开方乘方计算,用构造函数F(x,y)=x2+y2−r2F(x,y)=x^2+y^2-r^2F(x,y)=x2+y2−r2
{F(x,y)=0(圆上的点)F(x,y)>0(圆外的点)F(x,y)<0(圆内的点) \left\{
\begin {aligned}
F(x,y)=0(圆上的点)\\
F(x,y)>0(圆外的点)\\
F(x,y)<0(圆内的点)\\
\end {aligned}
\right.
⎩⎪⎨⎪⎧F(x,y)=0(圆上的点)F(x,y)>0(圆外的点)F(x,y)<0(圆内的点)
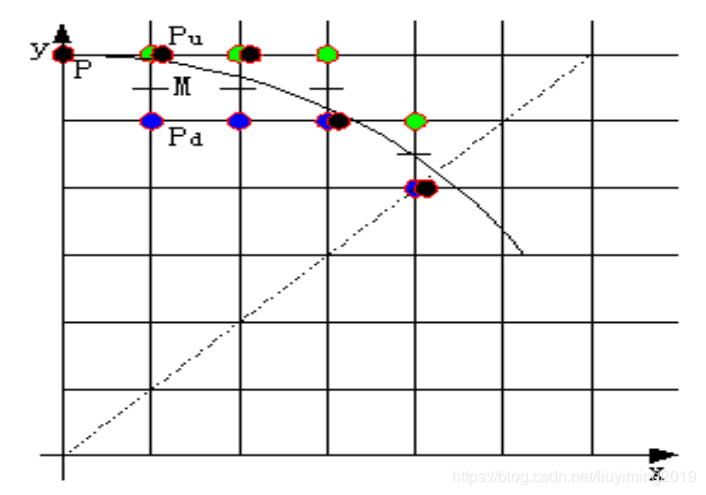
选取衡量标准,判断下一点是在(xi+1,yi)(x_i+1,y_i)(xi+1,yi)还是(xi+1,y+i)(x_i+1,y+i)(xi+1,y+i),用m(xi+1,yi−0.5)m(x_i+1,y_i-0.5)m(xi+1,yi−0.5)代入得判别式:
d=F(xm,ym)=F(xi+1,yi−0.5)=(xi+1)2+(yi−0.5)2−R2 \begin{aligned}
d&=F(x_m,y_m)\\
&=F(x_i+1,y_i-0.5) \\
&=(x_i+1)^2+(y_i-0.5)^2-R^2
\end{aligned} d=F(xm,ym)=F(xi+1,yi−0.5)=(xi+1)2+(yi−0.5)2−R2
d≤0d\leq0d≤0时,下一点为Pu(xi+1,yi)P_u(x_i+1,y_i)Pu(xi+1,yi),而我们真正关心的是求出误差项的递推公式,下面来推导:
dnew=F(xi+2,yi−0.5)=(xi+2)2+(yi−0.5)2−R2=(xi+1)2+(yi−0.5)2−R2+2xi+3=dold+2xi+3 \begin{aligned}
d_{new}&=F(x_i+2,y_i-0.5)\\
&=(x_i+2)^2+(y_i-0.5)^2-R^2\\
&=(x_i+1)^2+(y_i-0.5)^2-R^2+2x_i+3\\
&=d_{old}+2x_i+3
\end{aligned} dnew=F(xi+2,yi−0.5)=(xi+2)2+(yi−0.5)2−R2=(xi+1)2+(yi−0.5)2−R2+2xi+3=dold+2xi+3
同理,d>0d>0d>0时:
dnew=F(xi+2,yi−1.5)=(xi+2)2+(yi−1.5)2−R2=(xi+1)2+(yi−0.5)2−R2+(2xi+3)+(2−2yi)=dold+2(xi−yi)+5 \begin{aligned}
d_{new}&=F(x_i+2,y_i-1.5)\\
&=(x_i+2)^2+(y_i-1.5)^2-R^2\\
&=(x_i+1)^2+(y_i-0.5)^2-R^2+(2x_i+3)+(2-2y_i)\\
&=d_{old}+2(x_i-y_i)+5
\end{aligned} dnew=F(xi+2,yi−1.5)=(xi+2)2+(yi−1.5)2−R2=(xi+1)2+(yi−0.5)2−R2+(2xi+3)+(2−2yi)=dold+2(xi−yi)+5
这里讨论的是按顺时针方向生成第一个八分圆。则第一个象素是:(0,r)(0,r)(0,r),故得d0d_0d0:
d0=F(1,R−0.5)=1+(R−0.5)2−R2=1.25−R\begin{aligned}
d_0&=F(1,R-0.5)\\&=1+(R-0.5)^2-R^2\\&=1.25-R
\end{aligned} d0=F(1,R−0.5)=1+(R−0.5)2−R2=1.25−R
{d0=1−Rdnew=dold+2xi+3(d≤0)dnew=dold+2(xi−yi)+5(d>0) \left\{ \begin{aligned} &d_0= 1-R\\ &d_{new}=d_{old}+2x_i+3(d\leq0) \\ &d_{new}=d_{old}+2(x_i-y_i)+5(d > 0) \end{aligned} \right. ⎩⎪⎨⎪⎧d0=1−Rdnew=dold+2xi+3(d≤0)dnew=dold+2(xi−yi)+5(d>0) 这里研究的圆心都在(0,0)(0,0)(0,0)点,画任一(xc,yc)(x_c,y_c)(xc,yc)点即是分别向x,yx,yx,y方向进行了平移。
考虑14\frac{1}{4}41 象限的四分圆,此处以第一象限为例,每一点的下一个象素有三种选择,正右方(H)(H)(H),右下方(D)(D)(D),正下方(V)(V)(V)。观察发现以DDD的位置作为讨论依据最为科学。
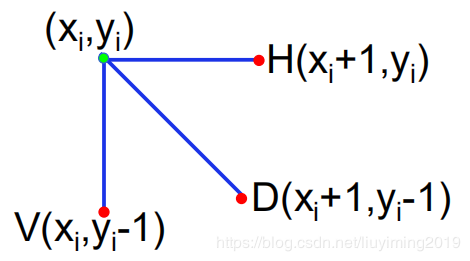
判断DDD点(注意是与圆上的距离不是圆心的距离)的位置:
ΔD=(x+1)2+(y+1)2−r2\Delta D=(x+1)^2+(y+1)^2-r^2ΔD=(x+1)2+(y+1)2−r2
接着判断D与E,D与F和圆周的相对距离大小判断涂色:
故公式为:
{ΔD=2−2rδHD=2ΔD+2y−1δDV=2ΔD−2x−1ΔD<0{δHD≤0⇒H点:ΔDnew=ΔDold+2(x+1)+1δHD>0⇒D点:ΔDnew=ΔDold+2(x+1)−2(y−1)+2ΔD>0{δHD≤0⇒D点:ΔDnew=ΔDold+2(x+1)−2(y−1)+2δHD>0⇒V点:ΔDnew=ΔDold+2(y−1)+1ΔD=0⇒D点:ΔDnew=ΔDold+2(x+1)−2(y−1)+2 \left\{ \begin{aligned} &\Delta D=2-2r\\ &\delta HD=2\Delta D+2y-1 \\&\delta DV=2\Delta D-2x-1\\ &\Delta D0\Rightarrow D点:\Delta D_{new}=\Delta D_{old}+2(x+1)-2(y-1)+2 \end{aligned} \right.\\ &\Delta D>0 \left\{ \begin{aligned} &\delta HD\leq0 \Rightarrow D点:\Delta D_{new}=\Delta D_{old}+2(x+1)-2(y-1)+2 \\ &\delta HD>0 \Rightarrow V点:\Delta D_{new}=\Delta D_{old}+2(y-1)+1 \end{aligned} \right.\\ &\Delta D=0\Rightarrow D点:\Delta D_{new}=\Delta D_{old}+2(x+1)-2(y-1)+2 \\ \end{aligned} \right. ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧ΔD=2−2rδHD=2ΔD+2y−1δDV=2ΔD−2x−1ΔD0⇒D点:ΔDnew=ΔDold+2(x+1)−2(y−1)+2ΔD>0{δHD≤0⇒D点:ΔDnew=ΔDold+2(x+1)−2(y−1)+2δHD>0⇒V点:ΔDnew=ΔDold+2(y−1)+1ΔD=0⇒D点:ΔDnew=ΔDold+2(x+1)−2(y−1)+2 优点:每次在三个点中判断,走样较小,可以一次处理四分之一圆。
类同于中点画圆法,区别是画第一象限的四分之一椭圆弧,关键是找到临界点。
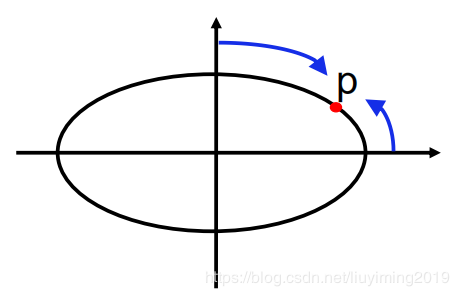
找到切线斜率为111的点p(xp,yp)p(x_p,y_p)p(xp,yp),利用中点画线法进行处理:
{xp=a2a2+b2yp=b2a2+b2 \left\{
\begin{aligned}
&x_p= \frac{a^2}{\sqrt{a^2+b^2}}\\
&y_p= \frac{b^2}{\sqrt{a^2+b^2}}
\end{aligned}
\right.
⎩⎪⎪⎪⎨⎪⎪⎪⎧xp=a2+b2a2yp=a2+b2b2
将14\frac{1}{4}41椭圆分成(0,b)(0,b)(0,b)到ppp点,(a,0)(a,0)(a,0)到ppp点两块,故公式为:
{(0,b)到p点:{d0=b2+(−b+0.25)a2dnew=dold+(2x+3)b2(d≤0)dnew=dold+(2x+3)b2+(2−2y)a2(d>0)(a,0)到p点:{d0=(−a+0.25)b2+a2dnew=dold+(2y+3)a2(d≤0)dnew=dold+(2y+3)a2+(2−2x)b2(d>0) \left\{
\begin{aligned}
&(0,b)到p点:
\left\{
\begin{aligned}
&d_0=b^2+(-b+0.25)a^2\\
&d_{new}=d_{old}+(2x+3)b^2(d\leq0)\\
&d_{new}=d_{old}+(2x+3)b^2+(2-2y)a^2(d>0)
\end{aligned}
\right.\\
&(a,0)到p点:
\left\{
\begin{aligned}
&d_0=(-a+0.25)b^2+a^2\\
&d_{new}=d_{old}+(2y+3)a^2(d\leq0)\\
&d_{new}=d_{old}+(2y+3)a^2+(2-2x)b^2(d>0)
\end{aligned}
\right.
\end{aligned}
\right.
⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧(0,b)到p点:⎩⎪⎨⎪⎧d0=b2+(−b+0.25)a2dnew=dold+(2x+3)b2(d≤0)dnew=dold+(2x+3)b2+(2−2y)a2(d>0)(a,0)到p点:⎩⎪⎨⎪⎧d0=(−a+0.25)b2+a2dnew=dold+(2y+3)a2(d≤0)dnew=dold+(2y+3)a2+(2−2x)b2(d>0)
线画图元的基本属性有线型、宽度和颜色。
线宽处理 线刷子 当斜率k∈[−1,1]k∈[-1,1]k∈[−1,1]之间,刷子置成垂直方向(水平方向刷),刷子的中点对准直线一端点,然后让刷子中心往直线的另一端移动,即可刷出具有一定宽度的线。 同理,当斜率k∉[−1,1]k\notin [-1,1]k∈/[−1,1]之间时,把刷子置成水平方向(竖直方向刷)。-
 引起的问题:汇合外角缺口
引起的问题:汇合外角缺口
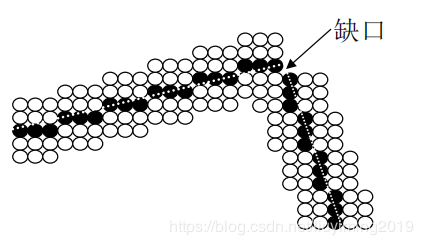
加圆帽,通过对每个方帽添加一个填充的半圆而得到。圆弧的圆心在线的端点其直径与线宽度相等。
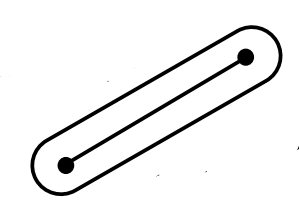
把边宽为指定线宽的正方形的中心沿直线作平行移动,用方形刷子绘制的线条比用线刷子绘制的要粗一些(对角线的原因)。
线刷子与方形刷子的对比: 线刷子在45°角附近线条在水平和垂直方向之间切换,最细 方形刷子正相反由于线宽正好为对角线而显著变粗 超链接如果你还想了解其他内容:
小白谈计算机图形学(一)如何画线
小白谈计算机图形学(二)如何画圆
小白谈计算机图形学(三)二维图形裁剪
作者:liuyiming2019