计算机图形学————viewing transform视图变换

学习目标

1、能够建立 相机坐标系
2、理解不同投影方式的特点
3、能建立所需的投影矩阵并用openGL实现
4、描述clipping的操作和函数

图像的产生过程

1、摆放好待拍摄的物品，或者人物。
这个时候物品或者人物就是在世界坐标系里，就是在一个公认的坐标系中，目的是保证待拍摄的物体和照相机在同一个坐标系
2、调整好拍摄角度。 WC->VC
这一步相当于视图变换，这时候的坐标就是camera coordinate system（VC） 这个过程是调整Camera到合适的位置以便拍摄，这里要计算View Matrix
3、调焦。 投影变换
4、拍摄。

要指定viewer坐标系，我们需要指定三个向量 VRP: view reference point 坐标系的原点（即摄像机的物理位置） VPN: View plane normal 给出相机指向的向量 vc的z轴 VUP: View UP Vector 定义胶片向上方向的矢量（图像） PRP:投影参考点

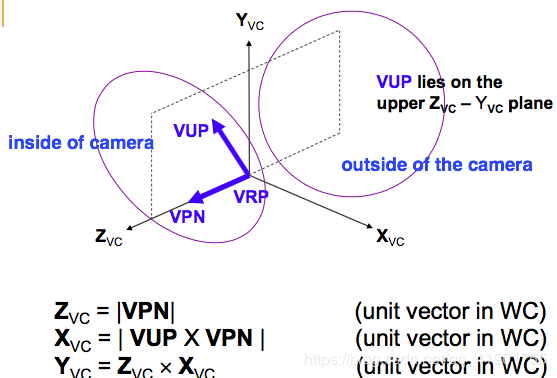
这三个向量都是在WC里的，不一定要是单位向量

从wc到vc的坐标表示

P(VC) = M（VC←WC）* P(WC)

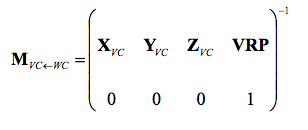
Note: XVC, YVC, ZVC 是WC中的单位列向量

在opengl中实现
glMatrixMode (GL_MODELVIEW);
gluLookAt (x0, y0, z0, xref, yref, zref, Vx, Vy, Vz);
VRP = (x0, y0, z0)
VPN = (x0, y0, z0) – (xref, yref, zref)
VUP = (Vx, Vy, Vz)
（x0，y0，z0）为放置相机的位置，
（xref，yref，zref）为场景的中心，
（Vx，Vy，Vz）记为一个矢量告诉相机的上在哪里

投影平面

view plane／ projection plane ／image plane

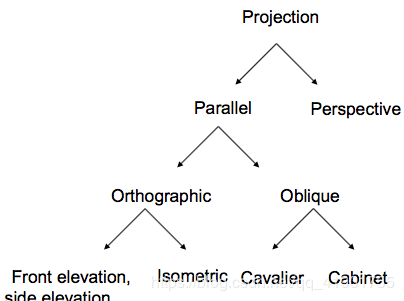
他是zvc=const 平行于xoy的一个平面 顾名思义，viwer坐标中的3D点（X，Y，Z）被投影到位于视平面上的2D点 投影分类

平行投影 parallel projections	透视投影 perspective projections

平行投影

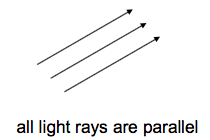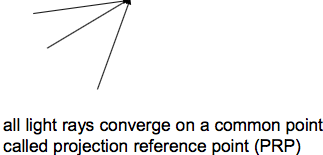正射投影Orthographic	斜投影oblique
投影向量⊥投影平面	投影向量不⊥投影平面
α = 90度	α ≠ 90度
两种表示：1、前测后视图和平面图 2、等轴测图（isometric）：投影平面的法向与每个坐标轴的夹角相等	1、斜等测投影cavalier projection :投影方向与投影平面成45度角，所以与投影平面垂直的直线段的投影与它本身的长度相等（xyz不变）；斜二测投影cabinet :投影方向和投影平面的夹角为arctan(2)，所以与投影平面垂直的直线段的长度是它投影长度的2倍。（投影后z减半）

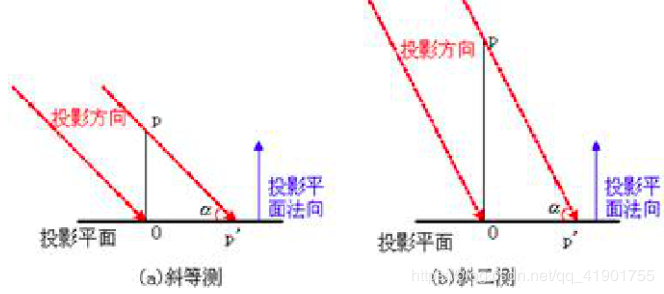
总结一下上面说到的投影方式，可以用下图表示

透视投影

所有光线都通过投影参考点（PRP），即投影中心。

物体修剪 clipping

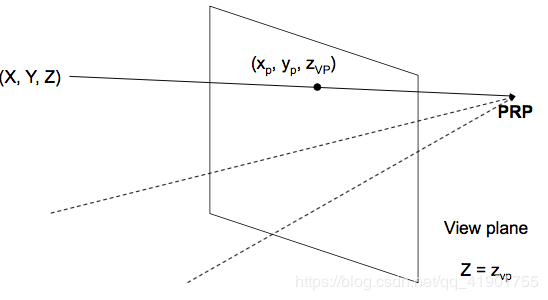
1、设置矩阵模式

glMatrixMode（GL_PROJECTION）;
注意：GL_PROJECTION用于处理投影 有两个4 x 4复合转换矩阵：GL_MODELVIEW和GL_PROJECTION 一个点预先乘以[GL_PROJECTION] [GL_MODELVIEW] glOrtho和gluPerspective

2、 关于正投影

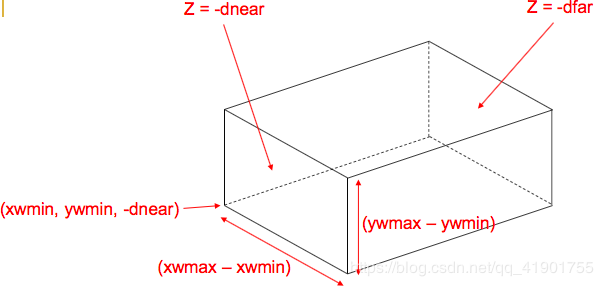
glOrtho（xwmin，xwmax，ywmin，ywmax，dnear，dfar）
投影向量Vp =（0，0，1）
裁剪平面：Z = -dnear Z = -dfar
裁剪平面附近的Z = -dnear也可以用作视平面
仅X和Y在| xwmin，xwmax |中的点和| ywmin，ywmax |被显示
裁剪出来的是一个矩形框
接下来只会对裁剪出的形状内的点进行操作

3、关于透视投影

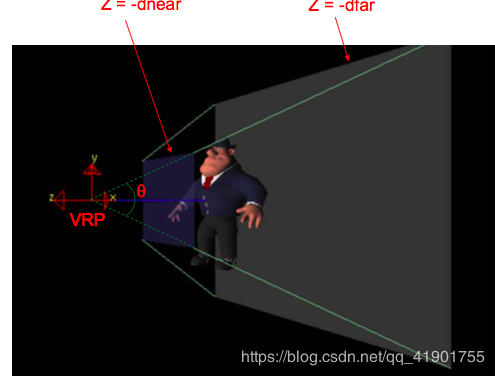
gluPerspective（theta，aspect，dnear，dfar）
PRP = VRP
Z = -dnear是视平面（请注意–ve符号）
dnear和dfar分别定义了近和远裁剪平面Z = -dnear和Z = -dfar
theta是视角
长宽比=（宽度/高度）
theta和aspect一起确定图像窗口的大小
裁剪量是一个平截头体
aspect 是蓝色区域里的 宽高比

作者：比风酷

计算机图形学 transform