小白谈计算机图形学（三）二维图形裁剪

Rosalia ·

更新时间:2024-11-13

· 620 次阅读

小白谈计算机图形学（三）二维图形裁剪引言如何裁剪Cohen-Sutherland代码裁剪算法基本思想Cohen-Sutherland操作步骤中点分割裁剪算法（对分法）基本思想线段和窗口有交点情况Liang－Barsky算法Liang的初发现如何判断入边出边?如何判断uuu值?Liang-Barsky算法特点超链接引言

管中窥豹，坐井观天，自然界中有一个个窗口让我们观察她的曼妙。计算机也有这样的窗口，让我们在全部中观察局部的现象。这里我们谈谈二维图形的裁剪。

如何裁剪

假定直线段用p1(x1,y1)p1(x1,y1)p1(x1,y1)、p2(x2,y2)p2(x2,y2)p2(x2,y2)表示。直线段和剪裁窗口的可能关系：

完全落在窗口内完全落在窗口外与窗口边界相交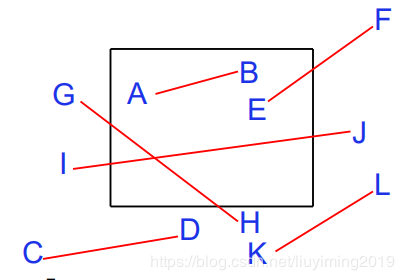
在这里插入图片描述

Cohen-Sutherland代码裁剪算法 基本思想

以窗口为基准进行分区，再以D3D2D1D0D_3D_2D_1D_0D3D2D1D0 (上下右左) 以外赋1，以内赋0的二进制形式给每个区命名，随之进行位与运算进行分析。
在这里插入图片描述

Cohen-Sutherland操作步骤 code1=0且code2=0，则该线段在窗口内，取之。 code1和code2 按位进行与运算，其结果不为0，即code1&code2≠0，则两端点必在窗口外的同一部位，弃之。都不成立,此时需要求出直线段与窗口边界的交点，在交点处把线段一分为二，其中必有一段完全在窗口以外，弃之。根据交点位置赋予新的四位编码，直到code1=0且code2=0为止。

优点：利用编码的思想，实现了对完全可见和不可见直线段的快速接受和拒绝。
缺点：部分可见查找较慢。

中点分割裁剪算法（对分法） 基本思想

同样对直线段端点进行分区编码，对前两种情况进行一样的处理。

线段和窗口有交点情况 核心思想：通过二分法逼近来确定直线与窗口的交点,由于到达像素级别便不再可分，故不会无限循环下去。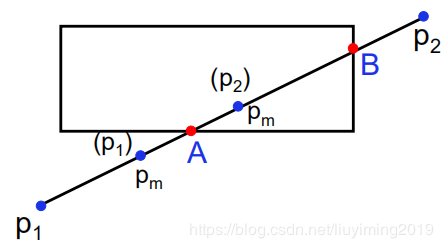
在这里插入图片描述

从p1p_1p1出发，找出离p1p_1p1最近的可见点AAA; 从p2p_2p2出发，找出离p2p_2p2最近的可见点BBB;ABABAB为p1p2p_1p_2p1p2的可见部分。

缺点：代码裁剪与矢量裁剪都要计算直线段与窗口边界的交点，大量乘除运算降低执行效率。

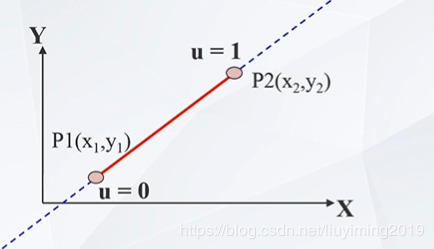
Liang－Barsky算法 Liang的初发现 用参数方程表示直线段
{x=x1+Δx∗uy=y1+Δy∗u(0≤u≤1) \left\{ \begin{aligned} x& = x_1+\Delta x*u\\ y& = y_1+\Delta y*u\\ (&0\leq u\leq1) \end{aligned} \right. ⎩⎪⎨⎪⎧xy(=x1+Δx∗u=y1+Δy∗u0≤u≤1)
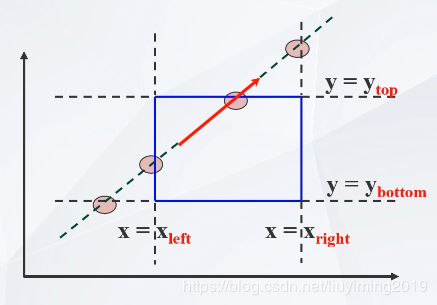
在这里插入图片描述

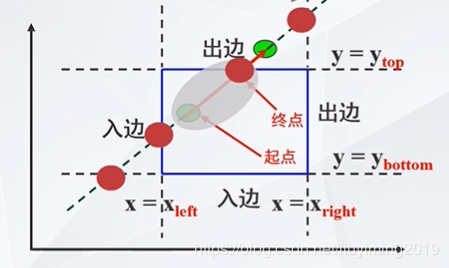把直线段看成一条有方向的线段，把窗口分为入边（直线由窗口外向窗口内移动，即左边界和下边界）和出边（直线由窗口内向窗口外移动，即右边界和上边界）加上自身总共666个点在这里插入图片描述

如何判断入边出边?如何判断uuu值?

判断一条线在窗口内的部分即判断窗口内点的取值范围，接下来所有推导将都会使用到起点p1(x1,y1)p_1(x_1,y_1)p1(x1,y1):
{xleft≤x1+Δx∗u≤xrightybottom≤y1+Δy∗u≤ytop \left\{ \begin{aligned} &x_{left} \leq x_1+\Delta x*u \leq x_{right}\\ &y_{bottom} \leq y_1+\Delta y*u \leq y_{top} \end{aligned} \right. {xleft≤x1+Δx∗u≤xrightybottom≤y1+Δy∗u≤ytop
我们得到点关于窗口四边的四个不等式，同时我们进行优化：
{p1=−Δxq1=x1−xLp2=Δxq2=xR−x1p3=−Δyq3=x1−xBp4=Δyq4=xT−x1 \left\{ \begin{aligned} &p_1 =-\Delta x &q_1=x_1-x_L\\ &p_2 =\Delta x &q_2=x_R-x_1\\ &p_3=-\Delta y &q_3=x_1-x_B\\ &p_4 =\Delta y &q_4=x_T-x_1\\ \end{aligned} \right. ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧p1=−Δxp2=Δxp3=−Δyp4=Δyq1=x1−xLq2=xR−x1q3=x1−xBq4=xT−x1

u∗pk≤qku*p_k\leq q_ku∗pk≤qk

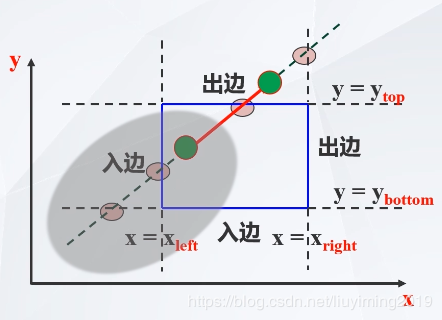
即满足上述条件就是我们寻找的点，那么我们想到当取等号即u=qkpku=\frac{q_k}{p_k}u=pkqk的时候，即是入边与出边四点：
在这里插入图片描述
那么如何判断入边和出边呢：由 pkp_kpk判断，这里不明白可以点击进行学习：
pk<0p_k<0pk<0时为入边，pk>0p_k>0pk>0时为出边，所以得Liang-Barsky算法的式子：
{p1=−Δxq1=x1−xLp2=Δxq2=xR−x1p3=−Δyq3=x1−xBp4=Δyq4=xT−x1u=qkpk \left\{ \begin{aligned} &p_1 =-\Delta x &q_1=x_1-x_L\\ &p_2 =\Delta x &q_2=x_R-x_1\\ &p_3=-\Delta y &q_3=x_1-x_B\\ &p_4 =\Delta y &q_4=x_T-x_1\\ &u=\frac{q_k}{p_k} \end{aligned} \right. ⎩⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎧p1=−Δxp2=Δxp3=−Δyp4=Δyu=pkqkq1=x1−xLq2=xR−x1q3=x1−xBq4=xT−x1

{umax=max(0,uk∣pk<0,uk∣pk<0)umin=min(1,uk∣pk>0,uk∣pk>0) \left\{ \begin{aligned} &u_{max}=max(0,u_{k|pk<0},u_{k|pk0},u_{k|pk>0})\\ \end{aligned} \right. {umax=max(0,uk∣pk<0,uk∣pk0,uk∣pk>0)
得到最大最小的值
在这里插入图片描述