假期无聊，我用傅里叶变换做了一个频率计，吉他定调口哨定音，样样好使！

Cady ·

更新时间:2024-11-14

· 736 次阅读

文章目录1. 前言2. 从正弦波开始3. 傅里叶变换的本质4. 解读傅里叶变换的结果5. 从声卡采集音频数据6. 音频频率计 1. 前言

当年《数学分析》考试通过后，那个高兴啊，心想，这一辈子总算再也不用和数学打交道了。没成想，新学期又开了一门叫做《工程数学》的专业课，专门讲傅里叶变换和拉普拉斯变换。全班同学为此郁闷了多半个学期。转眼间，三十多年过去了，拉氏变换早就还给了我的数学老师，唯独留下了傅里叶变换，偶尔还能有用武之地。这不，无聊的假期里，我用它做了一个音频的频率计，通过电脑上的声卡采集声音，用傅里叶变换完成时域-频域的转换，最后确定声音的主频率。用这个简陋的频率计来给吉他定调，比专业的定音器还好玩。

在娱乐中理解傅里叶变换、学习Python编程，这也许是一个很好的例子。你如果有兴趣亲自动手尝试一下的话，下面列出了必要的装备和技能。

电脑上得有声卡安装了pyAudio模块，用于采集声音安装了NumPy和SciPy模块，用于数据处理有一颗勇于探索的心，还要多少懂一点Python语法

NumPy和SciPy模块直接使用pip命令安装即可，安装pyAudio模块，请点这里下载相应版本的whl文件，然后使用pip命令在本地安装。

2. 从正弦波开始

在[0,4π][0, 4\pi][0,4π]之间，以均匀间隔取17点（包括首尾），并计算这17个点的正弦值：

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> x = np.linspace(0, 4*np.pi, 17)
>>> y = np.sin(x)
>>> plt.plot(y, c='m', marker='o')
[]
>>> plt.show()

因为数据取样点较少，所以曲线不够平滑，但仍然一眼就可以看出这是正弦波的两个完整周期。
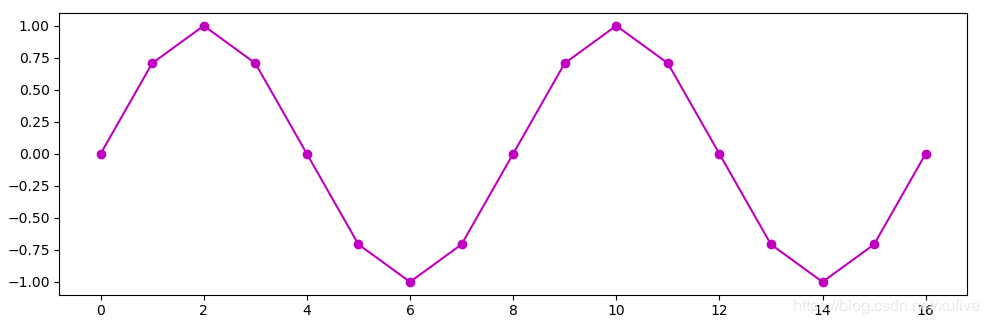
在这里插入图片描述
这个数据是静态的，看似和时间没有任何关系。不过，当我们假定这个数据是以0.125秒的时间间隔，在1秒钟内测量的某个周期性正弦波信号的的记录，那么，从这个记录就可以解读出两个非常重要的概念：信号周期和采样频率。

这个信号的周期是0.5s，频率是2Hz 这个数据的采样频率是16Hz

事实上，只要采样频率大于信号最高频率的两倍，就不会丢失信号的频率信息。这就是大名鼎鼎的采样定理，又称香农采样定理，或者奈奎斯特采样定理。采样定理架起了模拟信号和离散信号之间的桥梁，使得我们可以用一组离散的数据表示一个连续的模拟信号。

3. 傅里叶变换的本质

采样定理已经够牛B的了，但是傅里叶变换更神奇。在这里我尝试不用任何的数学概念去解释它，只从物理意义上描述这个充满魔性的傅里叶变换：任何一种周期性变化的连续信号，都可以分解成若干个不同振幅，不同相位的正弦波。傅里叶变换的本质，就是把一个在时间轴上连续变化的周期性信号（时域），分解成多个不同频率不同相位的正弦波信号（频域），也就是我们通常所说的时域到频域的转换。

但是，连续的模拟信号数据量太大，也不方便存储和处理，实际应用中，使用的都是离散傅里叶变换（Discrete Fourier Transform），简称DFT。即便是DFT，计算量也非常巨大，SciPy模块给我们提供了计算量更小的快速傅里叶变换（FFT）算法。

4. 解读傅里叶变换的结果

尽管NumPy也有傅里叶变换功能，但和SciPy模块的傅里叶变换显然不是同一个，我建议还是要从SciPy模块导入傅里叶变换子模块。使用快速傅里叶变换函数fft()对刚才生成的、采样频率为16Hz、长度为1秒钟的离散数据进行处理，我们得了一个和输入数据等长的复数型数组。

>>> import numpy as np
>>> from scipy import fft as spfft
>>> x = np.linspace(0, 4*np.pi, 17)
>>> y = np.sin(x)
>>> spfft.fft(y)
array([-9.99200722e-16-0.j        ,  1.05937589e-01-0.56671605j,
        2.89241705e+00-7.46618906j, -7.49750408e-01+1.21088849j,
       -5.21977137e-01+0.57258164j, -4.59137182e-01+0.3467243j ,
       -4.32617387e-01+0.21541786j, -4.20047836e-01+0.11951391j,
       -4.14824690e-01+0.03843917j, -4.14824690e-01-0.03843917j,
       -4.20047836e-01-0.11951391j, -4.32617387e-01-0.21541786j,
       -4.59137182e-01-0.3467243j , -5.21977137e-01-0.57258164j,
       -7.49750408e-01-1.21088849j,  2.89241705e+00+7.46618906j,
        1.05937589e-01+0.56671605j])

如何解读这个转换结果呢？仔细观察这个对采样频率为16Hz、长度为1秒钟的离散数据进行傅里叶变换后返回的数组，你会发现其中的一些规律：

数组长度和原始离散数据长度一致，其长度等于采样频率加1 元素类型是复数，每个元素都有实数和虚数两部分组成如果去掉第1个元素（索引为0的元素），剩余元素的第1个和最后1个相同，第2个和倒数第2个相同，……

原来，这个数组的元素，对应着信号分解后的各个不同频率不同相位的正弦波信号，实数表示振幅，虚数表示相位，相当于复数平面上的一个向量。数组的前一半元素中（后一半元素和前面重复），索引为0的元素，对应频率为0的信号，也就是直流信号，相位自然永远是0了；索引为k的元素，对应频率为k的信号。除了直流分量外，这些元素对应的信号中最强的那个信号分量的频率，就是原始信号的频率。

普遍情况下，对于采样频率为FnF_nFn、时间长度为TTT的离散数据进行傅里叶变换，返回的复数型数组的前一半元素，对应着信号分解后的各个不同频率不同相位的正弦波信号，元素的索引序号与时间长度TTT的比值，即为该元素对应的信号频率。

那么，如何考察信号分量的强度呢？我们就用复数平面上的一个向量的大小来表示这个向量对应的信号分量的强度。NumPy的绝对值函数np.abs()可以很漂亮的完成这个任务。为了使比较更有普遍性，还需要对这个结果做标准化处理，即除以采样数量。

>>> dforce = np.abs(spfft.fft(y))/17
>>> dforce
array([5.87765131e-17, 3.39136829e-02, 4.70992677e-01, 8.37771099e-02,
       4.55762744e-02, 3.38439680e-02, 2.84284240e-02, 2.56893715e-02,
       2.45059906e-02, 2.45059906e-02, 2.56893715e-02, 2.84284240e-02,
       3.38439680e-02, 4.55762744e-02, 8.37771099e-02, 4.70992677e-01,
       3.39136829e-02])
>>> plt.plot(dforce[:9])
[]
>>> plt.show()

下图是这个信号的频谱图，明显看出，时间长度为1秒的前提下，频率为2Hz分量的强度最大。
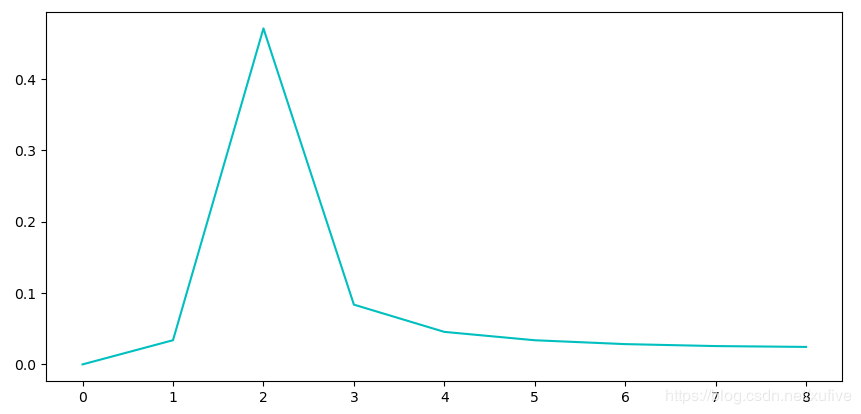
在这里插入图片描述
通过上面这些分析，我们就可以从音频数据中找出它的主频率了，前提是我们要知道这个音频信号的采样频率——通过采样频率和数据总数就可以算出信号时长。接下来的问题是，我们如何获取声音的数据？

5. 从声卡采集音频数据

pyAudio是我推荐给大家的一个用于声卡操作的模块，功能非常强悍。我们今天只用到了其中很少的一点点，就是采集声音。下面这段代码，演示了如何从声卡上读取固定长度（采样数）的声音数据。

import pyaudio as pa
import numpy as np
import matplotlib.pyplot as plt
def capture(secs, rate=8000, chunk=1024, idle=0):
    """采集声音数据
    secs    - 采样时长（秒）
    rate    - 采样频率
    idle    - 为了消除噪声，忽略起始信号的时长（秒）
    """
    data = b''
    idle_len, valid_len = int(2*rate*idle), int(2*rate*secs)+2
    ac = pa.PyAudio()
    stream = ac.open(
        format = pa.paInt16,            # 设置量化精度：每个采样数据占用的位数（2字节）
        channels = 1,                   # 设置单声道模式           
        rate = rate,                    # 设置采样频率
        frames_per_buffer = chunk,       # 设置声卡读写缓冲区     
        input = True                    # 设置声卡输出模式
    )
    while len(data) < idle_len + valid_len:
        data += stream.read(chunk)
    data = np.frombuffer(data[idle_len:idle_len+valid_len], dtype=np.int16)
    stream.close()
    ac.terminate()
    return data
data = capture(0.2, rate=8000, chunk=1024, idle=3) # 采集0.2秒的声音，采样频率8000Hz
plt.plot(data)
plt.show()

这是我吹口哨的声音波形，时长0.2秒，采样频率8000Hz，采样数据总数1601个。为了消除噪声，裁掉了起始的3秒钟。
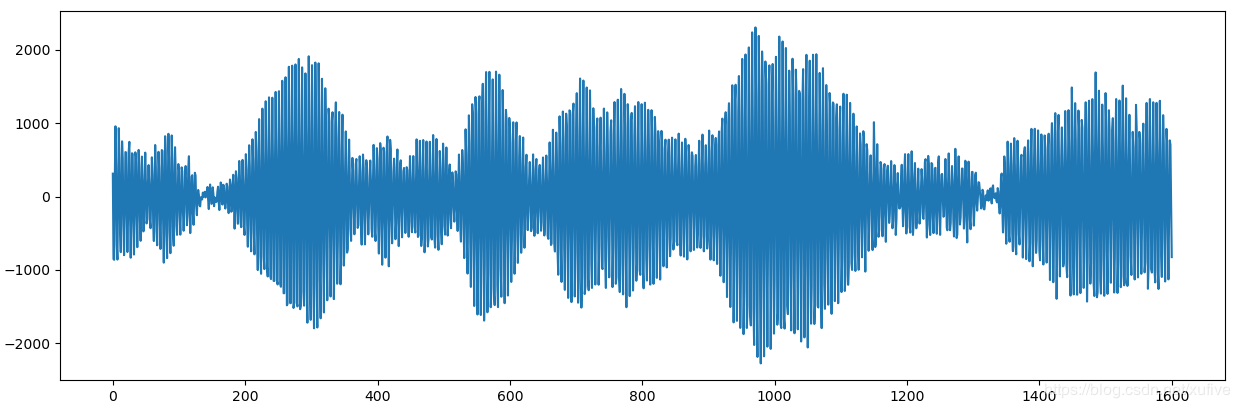
在这里插入图片描述

6. 音频频率计

获得声卡采集的数据后，只需要做傅里叶变换，取得最强信号分量的频率，即为采集到的这个数据的主频率。重复这个过程，就能不断地显示当前声音的频率。下面是全部代码。原以为会很长，没想到，写完只有区区五十余行。运行代码，试试了我那把民谣吉他，误差可以调整到到2Hz以内，堪比电子定音器。

# -*- encoding:utf-8 -*-
import pyaudio as pa
import numpy as np
from scipy import fft as spfft
def spectrum_analyser(data, rate):
    """频谱分析
    data    - 采集到的声音离散数据
    rate    - 采样频率
    """
    T = (data.shape[0]-1)/rate # 信号时长
    valid = int(np.ceil(data.shape[0]/2))
    dforce = np.abs(spfft.fft(data)[:valid])/data.shape[0]
    f = np.argmax(dforce)/T # 信号频率
    return f
def start(rate=8000, secs=0.5, idle=0.5, chunk=1024):
    """连续测试声音频率
    rate    - 采样频率
    secs    - 每次采样时长（秒）
    idle    - 为了消除噪声，每次采样忽略起始信号的时长（秒）
    chunk   - 声卡读写缓冲区大小
    """
    ac = pa.PyAudio()
    stream = ac.open(
        format = pa.paInt16,            # 设置量化精度：每个采样数据占用的位数（2字节）
        channels = 1,                   # 设置单声道模式           
        rate = rate,                    # 设置采样频率
        frames_per_buffer = chunk,      # 设置声卡读写缓冲区     
        input = True                    # 设置声卡输出模式
    )
    while True:
        data = b''
        idle_len, valid_len = int(2*rate*idle), int(2*rate*secs)+2
        while len(data) < idle_len + valid_len:
            data += stream.read(chunk)
        data = np.frombuffer(data[idle_len:idle_len+valid_len], dtype=np.int16)
        f = spectrum_analyser(data, rate)
        print(f)
if __name__ == '__main__':
    # 启动频率计
    start()

作者：天元浪子

频率计傅里叶变换

1024 个赞