【信号与系统学习笔记】—— 连续时间非周期信号傅里叶变换的性质 【下篇】(时域卷积定理和频域卷积定理)
我们先给出定理:两个时域信号做卷积,就等价于它们的频谱做乘法。
即:若:x(t) F↔ X(jω);y(t) F↔ Y(jω)x(t)\space \underleftrightarrow{\mathscr{F}} \space X(jω); \quad y(t)\space \underleftrightarrow{\mathscr{F}} \space Y(jω)x(t) F X(jω);y(t) F Y(jω);那么x(t)∗y(t) F↔ X(jω)Y(jω)x(t)*y(t) \space \underleftrightarrow{\mathscr{F}} \space X(jω)Y(jω)x(t)∗y(t) F X(jω)Y(jω)
这给我们计算一个系统的输出带来了极大的便利。我们可以先求出输入信号的频谱和系统的频率响应,两者一乘,最后做一下傅里叶逆变换就可以得出系统的输出(时域上的)。
【Proof】:我们下面证明一下,直接从定义出发:Y(jω)=∫−∞+∞y(t)e−jωtdt=∫−∞+∞[∫−∞+∞x(τ)h(t−τ)dτ]e−jωtdt
\begin{aligned}
Y(jω) &= \int_{-∞}^{+∞}y(t)e^{-jωt}dt\\
&=\int_{-∞}^{+∞}[\int_{-∞}^{+∞}x(τ)h(t - τ)dτ]e^{-jωt}dt\\\\
\end{aligned}
Y(jω)=∫−∞+∞y(t)e−jωtdt=∫−∞+∞[∫−∞+∞x(τ)h(t−τ)dτ]e−jωtdt
到这里,博主有话要说了:因为我们现在的被积函数是x(τ)x(τ)x(τ) 和 h(t−τ)h(t - τ)h(t−τ) 都是和 τττ 有关的表达式,因此我们不能简单粗暴地把它们拆开,一个是 ttt 的积分,另一个是 τττ 的积分。这样是错误的!!但是我们又注意到:只有 h(t−τ)h(t - τ)h(t−τ) 是和 ttt 有关的,那么我们确实可以先让 h(t−τ)h(t - τ)h(t−τ) 对 ttt 积分,dτdτdτ 放在最后面去做。
Y(jω)=∫−∞+∞[∫−∞+∞x(τ)h(t−τ)dτ]e−jωtdt=∫−∞+∞[x(τ)∫−∞+∞h(t−τ)e−jωtdt]dτ
\begin{aligned}
Y(jω) &=\int_{-∞}^{+∞}[\int_{-∞}^{+∞}x(τ)h(t - τ)dτ]e^{-jωt}dt\\
&=\int_{-∞}^{+∞}[x(τ)\int_{-∞}^{+∞}h(t - τ)e^{-jωt}dt]dτ
\end{aligned}
Y(jω)=∫−∞+∞[∫−∞+∞x(τ)h(t−τ)dτ]e−jωtdt=∫−∞+∞[x(τ)∫−∞+∞h(t−τ)e−jωtdt]dτ
这里我们需要用到傅里叶变换的延时特性:若 x(t) F↔ X(jω)x(t)\space \underleftrightarrow{\mathscr{F}} \space X(jω)x(t) F X(jω),那么 x(t−t0) F↔ X(jω)e−jωt0x(t-t_0) \space \underleftrightarrow{\mathscr{F}} \space X(jω)e^{-jωt_0}x(t−t0) F X(jω)e−jωt0
换成数学表达式就是:∫−∞+∞h(t−τ)e−jωtdt=H(jω)e−jωτ
\int_{-∞}^{+∞}h(t - τ)e^{-jωt}dt = H(jω)e^{-jωτ}∫−∞+∞h(t−τ)e−jωtdt=H(jω)e−jωτ
所以上式就变为:Y(jω)=∫−∞+∞[x(τ)∫−∞+∞h(t−τ)e−jωtdt]dτ=∫−∞+∞x(τ)e−jωτH(jω)dτ=H(jω)∫−∞+∞x(τ)e−jωτdτ=H(jω)X(jω)
\begin{aligned}
Y(jω) &=\int_{-∞}^{+∞}[x(τ)\int_{-∞}^{+∞}h(t - τ)e^{-jωt}dt]dτ\\
&=\int_{-∞}^{+∞}x(τ)e^{-jωτ}H(jω)dτ\\
&=H(jω)\int_{-∞}^{+∞}x(τ)e^{-jωτ}dτ\\
&=H(jω)X(jω)
\end{aligned}
Y(jω)=∫−∞+∞[x(τ)∫−∞+∞h(t−τ)e−jωtdt]dτ=∫−∞+∞x(τ)e−jωτH(jω)dτ=H(jω)∫−∞+∞x(τ)e−jωτdτ=H(jω)X(jω)
那么,问题来了:还记得我们在之前的 BlogBlogBlog 里面说过的吗?任何一个系统都可以通过其单位冲激响应 h(t)h(t)h(t) 来表征对吧,那么根据我们现在推导出的时域卷积定理:Y(jω)=H(jω)X(jω)Y(jω)=H(jω)X(jω)Y(jω)=H(jω)X(jω),那么按理说任何一个系统应该也可以用它的频率响应 H(jω)H(jω)H(jω) 来表征。但是,确实是这样吗?
我们知道,H(jω)H(jω)H(jω) 是 h(t)h(t)h(t) 的傅里叶变换,那么所以只有当 h(t)h(t)h(t) 满足傅里叶变换的收敛条件其中之一:∫−∞+∞∣h(t)∣2dt<∞ ∫−∞+∞∣h(t)∣dt<∞
\int_{-∞}^{+∞}|h(t)|^2dt < ∞\\
\space\\
\int_{-∞}^{+∞}|h(t)|dt < ∞∫−∞+∞∣h(t)∣2dt<∞ ∫−∞+∞∣h(t)∣dt<∞
那么,这个系统才会存在频率响应,也就是说,不是所有的系统都能够求出它的频率响应。那么也就不能说:任何系统都可以用它的频率响应 H(jω)H(jω)H(jω) 来表征。但是在本文后面的部分将会给出 h(t)h(t)h(t) 和 H(jω)H(jω)H(jω)(存在的情况)的计算方法。
我们先给出定理:若 x1(t),x2(t)x_1(t), x_2(t)x1(t),x2(t) 的傅里叶变换分别为:X1(jω),X2(jω)X_1(jω), X_2(jω)X1(jω),X2(jω),那么有:x1(t)⋅x2(t) F↔ 12πX1(jω)∗X2(jω) x_1(t)\sdot x_2(t) \space \underleftrightarrow{\mathscr{F}} \space \frac{1}{2π} X_1(jω) * X_2(jω) x1(t)⋅x2(t) F 2π1X1(jω)∗X2(jω)
2.1 应用:正弦幅度调制我们知道如果要计算系统的输出,我们可以通过时域卷积的方法计算得到。那么,什么场合下我们会用到时域信号相乘呢?答案就是—— 正弦幅度调制(当然不仅仅是这种,未来的 IQIQIQ 调制等等也都会用得上)
我们来看看正弦幅度调制的框图:
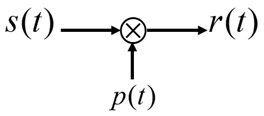
其中,s(t)s(t)s(t) 是我们的时域信号,p(t)=cos(ω0t)p(t) = cos(ω_0t)p(t)=cos(ω0t),那么得到的 r(t)r(t)r(t) 就是 s(t)⋅p(t)s(t)\sdot p(t)s(t)⋅p(t)
下面,我们就从频域的角度去分析正弦幅度调制:
【1】第一步:计算 p(t)p(t)p(t), s(t)s(t)s(t) 的频谱。
对于 cos(ω0t)cos(ω_0t)cos(ω0t) 的频谱我们应该是很熟悉了,即 P(jω)=πδ(ω+ω0)+πδ(ω−ω0)P(jω) = πδ(ω+ω_0) + πδ(ω-ω_0)P(jω)=πδ(ω+ω0)+πδ(ω−ω0),如下图所示:
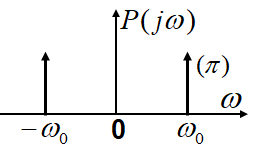
我们再假设信号 s(t)s(t)s(t) 的频谱如下图所示:
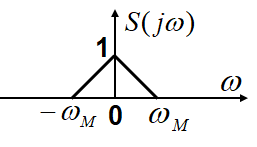
根据:x1(t)⋅x2(t) F↔ 12πX1(jω)∗X2(jω)x_1(t)\sdot x_2(t) \space \underleftrightarrow{\mathscr{F}} \space \frac{1}{2π} X_1(jω) * X_2(jω)x1(t)⋅x2(t) F 2π1X1(jω)∗X2(jω),我们可以知道两个信号相乘之后的频谱如下图所示:
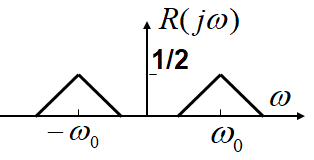
这里我们得出了一个结论:信号 s(t)s(t)s(t) 在时域上与 cos(ω0t)cos(ω_0t)cos(ω0t) 相乘,相当于在频谱上把 s(t)s(t)s(t) 的频谱一分为二之后,分别向左右各搬移 ω0ω_0ω0! (频谱搬移)
好的,到这里,我们已经了解了正弦幅度调制的细节。可以既然有调制,那么在接收端就必然需要解调。我们如何把这个调制的信号解调出来呢??
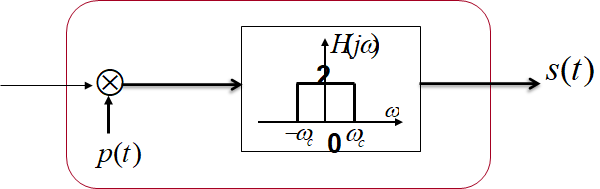
我们看到,最左边的箭头的输入,就是我们刚刚那个调制的信号,在解调端,我们需要再给这个信号乘以原载波 cos(ω0t)cos(ω_0t)cos(ω0t) ,然后经过一个低通滤波器(通带增益为2),就可以换原原本的信号了!
我们也是从频谱的角度来直观地看一下这个过程:
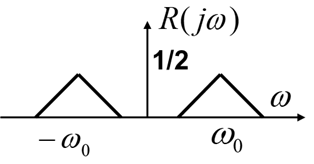
下图是输入信号 r(t)r(t)r(t) 的频谱:
下图是 p(t)p(t)p(t) 的频谱,r(t)r(t)r(t) 需要再和载波进行相乘:
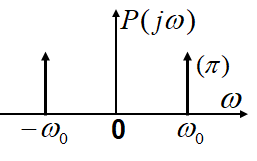
那么,二者相乘得到信号的频谱就是:
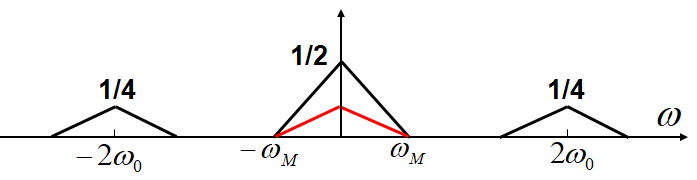
此时注意:中间频谱的幅度是 12\frac{1}{2}21
那么,经过一个通带增益为2的低通滤波器,就可以恢复原信号的频谱了!(下图为该低通滤波器的频响)
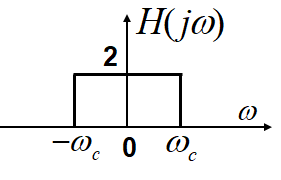
我们常常使用线性常系数微分方程来表征一个系统,如下:
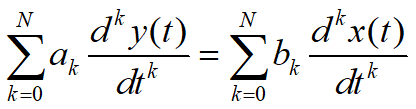
这时,我们可以直接对方程两边做傅里叶变换,根据傅里叶变换的微分性可以得出:∑k=0Nak(jω)kY(jω)=∑k=0Nbk(jω)kX(jω)
\sum_{k=0}^{N}a_k(jω)^kY(jω) = \sum_{k=0}^Nb_k(jω)^kX(jω)k=0∑Nak(jω)kY(jω)=k=0∑Nbk(jω)kX(jω)
同时,又根据:X(jω)H(jω)=Y(jω)X(jω)H(jω) = Y(jω)X(jω)H(jω)=Y(jω),所以我们可以得到系统的频率响应为:H(jω)=Y(jω)X(jω)=∑k=0Nbk(jω)k∑k=0Nak(jω)k
H(jω) = \frac{Y(jω)}{X(jω)} = \frac{\sum_{k=0}^Nb_k(jω)^k}{\sum_{k=0}^{N}a_k(jω)^k}H(jω)=X(jω)Y(jω)=∑k=0Nak(jω)k∑k=0Nbk(jω)k
【我们举一个例子来感受这种方法的简便性,同时也给大家介绍一种解题技法】:
求以下面这个微分方程表征的系统的 h(t)h(t)h(t):
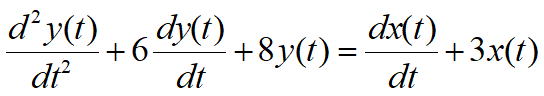
两边做傅里叶变换,得:(jω)2Y(jω)+6(jω)Y(jω)+8Y(jω)=(jω)X(jω)+3X(jω)((jω)2+6(jω)+8)Y(jω)=((jω)+3)X(jω)
(jω)^2Y(jω) + 6(jω)Y(jω) + 8Y(jω) = (jω)X(jω) + 3X(jω)\\
((jω)^2 + 6(jω) + 8)Y(jω) = ((jω) + 3)X(jω)(jω)2Y(jω)+6(jω)Y(jω)+8Y(jω)=(jω)X(jω)+3X(jω)((jω)2+6(jω)+8)Y(jω)=((jω)+3)X(jω)
因此,系统得频率响应可以表示为:H(jω)=Y(jω)X(jω)=(jω)+3(jω)2+6(jω)+8=jω+3(jω+2)(jω+4)
H(jω) = \frac{Y(jω)}{X(jω)} = \frac{(jω)+3}{(jω)^2 + 6(jω) + 8} = \frac{jω+3}{(jω+2)(jω+4)}H(jω)=X(jω)Y(jω)=(jω)2+6(jω)+8(jω)+3=(jω+2)(jω+4)jω+3
我们乍一看这个表达式看不能立刻得出结论,还需要使用下面这个技巧来分解一下:H(jω)=A1jω+2+A2jω+4=jω+3(jω+2)(jω+4)
H(jω) = \frac{A_1}{jω+2} + \frac{A_2}{jω+4} = \frac{jω+3}{(jω+2)(jω+4)}H(jω)=jω+2A1+jω+4A2=(jω+2)(jω+4)jω+3
下面就需要计算 A1,A2A_1, A_2A1,A2。下面是固定套路:
即:H(jω)=121jω+2+121jω+4 H(jω) = \frac{1}{2}\frac{1}{jω+2} + \frac{1}{2}\frac{1}{jω+4}H(jω)=21jω+21+21jω+41
还记得单边指数信号 e−atu(t)e^{-at}u(t)e−atu(t) 的频谱嘛?—— 1a+jω\frac{1}{a+jω}a+jω1
因此,我们看到这里:1jω+2\frac{1}{jω+2}jω+21 的原信号就是:e−2tu(t)e^{-2t}u(t)e−2tu(t)。所以 h(t)h(t)h(t) 为:h(t)=12e−2tu(t)+12e−4tu(t)
h(t) = \frac{1}{2}e^{-2t}u(t) + \frac{1}{2}e^{-4t}u(t)h(t)=21e−2tu(t)+21e−4tu(t)
【1】级联

还记得时域里面如果两个系统级联,那么它们的响应关系是:h1(t)∗h2(t)h_1(t) * h_2(t)h1(t)∗h2(t)
根据时域卷积定理,它们的频域关系就是:H1(jω)H2(jω)H_1(jω)H_2(jω)H1(jω)H2(jω)
【2】并联:并联里面时域和频域都一样,都是相加。
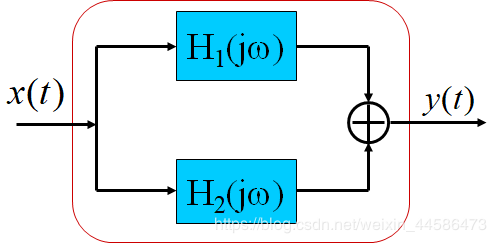
H1(jω)+H2(jω)H_1(jω) + H_2(jω)H1(jω)+H2(jω)
作者:凝望,划过星空.scut