傅里叶变换、离散傅里叶变换(DFT)、快速傅里叶变换(FFT)详解
以下内容参考《复变函数与积分变换》,如果对积分变换有所了解,完全可以跳过忽略
复数的三角表达式如下
Z=r(cosθ+isinθ)
Z=r(cos\theta+isin\theta)
Z=r(cosθ+isinθ)
欧拉公式如下
eiθ=cosθ+isinθ
e^{i\theta}=cos\theta+isin\theta
eiθ=cosθ+isinθ
所以,两式连立,我们可以得到复数的指数表达式
Z=reiθ
Z=re^{i\theta}
Z=reiθ
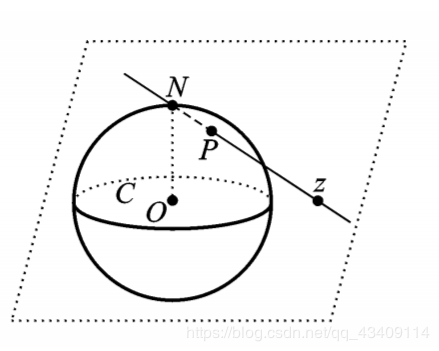
复球面如下图,除了N点以外,任意一个复数都与复球面上的点一一对应。
对于任意复数z的乘幂有下列公式成立
Zn=rneinθ
Z^n=r^ne^{in\theta}
Zn=rneinθ
当r=1时,我们可得到De Moivre公式
(cosθ+isinθ)N=cosNθ+isinNθ
(cos\theta+isin\theta)^N=cos N\theta +isinN\theta
(cosθ+isinθ)N=cosNθ+isinNθ
复数的方根

复变函数的几何解释
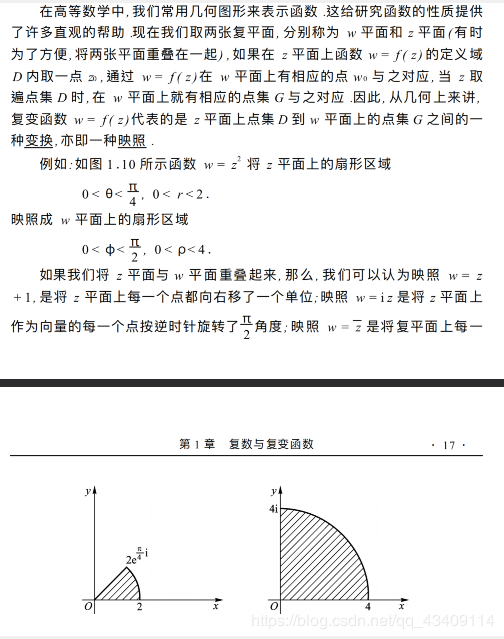
复变函数中的常用初等函数
1. 指数函数

对数函数

幂函数

三角函数

在高等数学中我们就已经学习过傅里叶级数了,书中是这么描述的任何周期函数都可以用正弦函数和余弦函数构成的无穷级数来表示,公式是下面这样描述的
f(t)=a0+∑n=1∞[ancos(nωt)+bncos(nωt)]
f(t)=a_0+\sum^{\infty}_{n=1}[a_ncos(n\omega t)+b_ncos(n\omega t)]
f(t)=a0+n=1∑∞[ancos(nωt)+bncos(nωt)]
其中
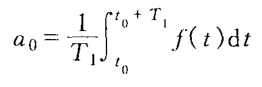
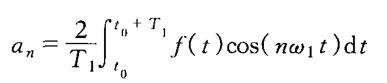
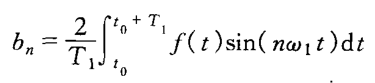
上面的推导过程是利用三角函数集的正交性进行的,推导过程很简单,就不再说了。如果想看看推导过程的请点击这里
我们可以用上面提到的复数知识,将上述的正余弦形式的傅里叶级数,改写成复指数形式的傅里叶级数,过程如下:
欧拉公式如下
eiθ=cosθ+isinθ
e^{i\theta}=cos\theta+isin\theta
eiθ=cosθ+isinθ
通过上述欧拉公式,得到余弦、正弦的复指数表达,如下
sinθ=eix−e−ix2i
sin \theta=\frac{e^{ix}-e^{-ix}}{2i}
sinθ=2ieix−e−ix
cosθ=eix+e−ix2
cos \theta=\frac{e^{ix}+e^{-ix}}{2}
cosθ=2eix+e−ix
将上述公式代入傅里叶级数中,可以得到
f(t)=a0+∑n=0∞(an−ibn2einω1t+an+ibn2e−inω1t)
f(t)=a_0+\sum^{\infty}_{n=0}(\frac{a_n-ib_n}{2}e^{in\omega_1t}+\frac{a_n+ib_n}{2}e^{-in\omega_1t})
f(t)=a0+n=0∑∞(2an−ibneinω1t+2an+ibne−inω1t)
为了将上述式子合并
F(nω1)=an+ibn2e−inω1t
F(n\omega_1)=\frac{a_n+ib_n}{2}e^{-in\omega_1t}
F(nω1)=2an+ibne−inω1t
F(−nω1)=a−n−ib−n2einω1t
F(-n\omega_1)=\frac{a_{-n}-ib_{-n}}{2}e^{in\omega_1t}
F(−nω1)=2a−n−ib−neinω1t
且当n=0的时候,bn=0,an=a0,e−i0ω1t=1,所以F(0)=a02
且当n=0的时候,b_n=0,a_n=a_0,e^{-i0\omega_1t}=1,所以F(0)=\frac{a_0}{2}
且当n=0的时候,bn=0,an=a0,e−i0ω1t=1,所以F(0)=2a0
所以上述式子可以合并成
f(t)=∑n=−∞∞an+ibn2e−inω1t
f(t)=\sum^{\infty}_{n=-\infty}\frac{a_n+ib_n}{2}e^{-in\omega_1t}
f(t)=n=−∞∑∞2an+ibne−inω1t
化简一下
f(t)=∑n=−∞∞F(nω1)einω1t
f(t)=\sum^{\infty}_{n=-\infty}F(n\omega_1)e^{in\omega_1t}
f(t)=n=−∞∑∞F(nω1)einω1t
我们再把an,bna_n,b_nan,bn代入FFF中,可以得出最终傅里叶级数变换式
F(nω1)=1T1∫t0t0+Tf(t)e−inω1tdt
F(n\omega_1)=\frac{1}{T_1}\int ^{t_0+T}_{t_0}f(t)e^{-in\omega_1t}dt
F(nω1)=T11∫t0t0+Tf(t)e−inω1tdt
f(t)=∑n=−∞∞F(nω1)einω1t
f(t)=\sum^{\infty}_{n=-\infty}F(n\omega_1)e^{in\omega_1t}
f(t)=n=−∞∑∞F(nω1)einω1t
根据前述的傅里叶级数可知,任何周期函数,都可以由正弦、余弦函数共同组合而成。现在假设有一个函数(信号)f(t)f(t)f(t),其周期为T1T_1T1,角频率为W1W_1W1。那么我们可以表示成如下形式。
f(t)=a02+∑n=0∞[ancos(nω1t)+bnsin(nω1t)]
f(t)=\frac{a_0}{2}+\sum^{\infty}_{n=0}[a_ncos(n\omega_1t)+b_nsin(n\omega_1t)]
f(t)=2a0+n=0∑∞[ancos(nω1t)+bnsin(nω1t)]
其中a0,an,bna_0,a_n,b_na0,an,bn都已经计算出来了。
但上面是傅里叶级数,并非是傅里叶变换,所谓傅里叶变换就是将傅里叶级数的分析方法给推广到任何函数中,即非周期函数中。
但是如果TTT趋于无穷,那么就会导致谱线长度变成0,所以此时,必须要引入一个新的量,称为频谱密度函数
我们将F(nω1)F(n\omega_1)F(nω1)两边同时乘以T_1
T1F(nω1)=∫t0t0+Tf(t)e−inω1tdt
T_1F(n\omega_1)=\int ^{t_0+T}_{t_0}f(t)e^{-in\omega_1t}dt
T1F(nω1)=∫t0t0+Tf(t)e−inω1tdt
如果该函数的不是周期函数,那么T−>∞,ω1−>0T->\infty ,\omega_1->0T−>∞,ω1−>0,所以nω1n\omega_1nω1就趋于连续值了,我们可以用ω\omegaω代替,谱线间隔△nω1\bigtriangleup n \omega_1△nω1也可以描述为dωd\omegadω。
那么这时,我们将F(nω1)F(n\omega_1)F(nω1)改成如下形式
F(ω)=T1F(nω1)=limT1→∞∫−T2T2f(t)e−inω1tdt
F(\omega)=T_1F(n\omega_1)=\lim_{T_1\to\infty}\int ^{\frac{T}{2}}_{-\frac{T}{2}}f(t)e^{-in\omega_1t}dt
F(ω)=T1F(nω1)=T1→∞lim∫−2T2Tf(t)e−inω1tdt
所以,最终我们得到了傅里叶变换
F(ω)=∫−∞+∞f(t)e−iωtdt
F(\omega)=\int ^{+\infty}_{-\infty}f(t)e^{-i\omega t}dt
F(ω)=∫−∞+∞f(t)e−iωtdt
我们也说上面的傅里叶变换是广义傅里叶变换。
思考一下,为什么我们也称其为频谱密度函数,那是因为T1F(nω1)=2πF(nω1)ω1T_1F(n\omega_1)=\frac{2\pi F(n\omega_1)}{\omega_1}T1F(nω1)=ω12πF(nω1),其中F(nω1)ω1\frac{F(n\omega_1)}{\omega_1}ω1F(nω1)指的是单位频宽下的谱线长度,也就是频谱密度
最后我们再对傅里叶反变换进行一下改变就行了
ω1→0
\omega_1 \to0 \\
ω1→0
nω1→w
n\omega_1 \to w
nω1→w
△(nω1)→dw
\bigtriangleup (n\omega_1) \to dw
△(nω1)→dw
∑ω=−∞∞dω=∫−∞+∞dω
\sum^{\infty}_{\omega=-\infty}d\omega=\int ^{+\infty}_{-\infty}d\omega
ω=−∞∑∞dω=∫−∞+∞dω
f(t)=∑nω1=−∞∞F(nω1)ω1einω1tω1=∑nω1=−∞∞F(nω1)ω1einω1tdω=∑ω=−∞∞F(ω)2πeinω1tdω=12π∫−∞+∞F(ω)eiωtdω
\begin{array}{ll}
f(t)&=\sum^{\infty}_{n\omega_1=-\infty}\frac{F(n\omega_1)}{\omega_1}e^{in\omega_1t}\omega_1 \\
&\\
&=\sum^{\infty}_{n\omega_1=-\infty}\frac{F(n\omega_1)}{\omega_1}e^{in\omega_1t}d\omega\\
&\\
&=\sum^{\infty}_{\omega=-\infty}\frac{F(\omega)}{2\pi}e^{in\omega_1t}d\omega&\\
&\\
&=\frac{1}{2\pi}\int ^{+\infty}_{-\infty}F(\omega)e^{i\omega t}d\omega
\end{array}
f(t)=∑nω1=−∞∞ω1F(nω1)einω1tω1=∑nω1=−∞∞ω1F(nω1)einω1tdω=∑ω=−∞∞2πF(ω)einω1tdω=2π1∫−∞+∞F(ω)eiωtdω
总结一下,傅里叶变换和傅里叶反变换,如下
F(ω)=∫−∞+∞f(t)e−iωtdt
F(\omega)=\int ^{+\infty}_{-\infty}f(t)e^{-i\omega t}dt
F(ω)=∫−∞+∞f(t)e−iωtdt
f(t)=12π∫−∞+∞F(ω)eiωtdω
f(t)=\frac{1}{2\pi}\int ^{+\infty}_{-\infty}F(\omega)e^{i\omega t}d\omega
f(t)=2π1∫−∞+∞F(ω)eiωtdω
在学习DFT之前,先了解以下离散傅里叶级数对于过度到DFT是很有帮助的。两者之间主要的区别就是,离散傅里叶级数是用来分析周期序列,而离散傅里叶变换是用来分析有限长序列
现在假设有一个周期序列:xp(n)=xp(n+rN)x_p(n)=x_p(n+rN)xp(n)=xp(n+rN),其周期为NNN。定义这个周期序列的离散傅里叶级数完全可以参照连续傅里叶级数。
先看看之前推导的傅里叶级数的公式
F(nω1)=1T1∫t0t0+Tf(t)e−inω1tdt
F(n\omega_1)=\frac{1}{T_1}\int ^{t_0+T}_{t_0}f(t)e^{-in\omega_1t}dt
F(nω1)=T11∫t0t0+Tf(t)e−inω1tdt
f(t)=∑n=−∞∞F(nω1)einω1t
f(t)=\sum^{\infty}_{n=-\infty}F(n\omega_1)e^{in\omega_1t}
f(t)=n=−∞∑∞F(nω1)einω1t
我们可以把1T1\frac{1}{T_1}T11给提到f(t)f(t)f(t)里面去,最后就会变成下面那样
F(nω1)=∫t0t0+Tf(t)e−inω1tdt
F(n\omega_1)=\int ^{t_0+T}_{t_0}f(t)e^{-in\omega_1t}dt
F(nω1)=∫t0t0+Tf(t)e−inω1tdt
f(t)=1T1∑n=−∞∞F(nω1)einω1t
f(t)=\frac{1}{T_1}\sum^{\infty}_{n=-\infty}F(n\omega_1)e^{in\omega_1t}
f(t)=T11n=−∞∑∞F(nω1)einω1t
ok,现在我们通过改写上面的公式,使其支持离散周期序列。因为是离散的,所以积分符号∫t0t0+T\int ^{t_0+T}_{t_0}∫t0t0+T要变成求和符合∑n=0N−1\sum^{N-1}_{n=0}∑n=0N−1,周期函数的频率ω1\omega_1ω1要变成2πN\frac{2\pi}{N}N2π,周期T1T_1T1也要变成NNN,无限求和∑n=−∞∞\sum^{\infty}_{n=-\infty}∑n=−∞∞也要变成有限的∑n=0N−1\sum^{N-1}_{n=0}∑n=0N−1。
最终改写出来的结果如下
X[k]=∑n=0N−1f(t)(e−ik(2πN))n【1式】
X[k]=\sum^{N-1}_{n=0}f(t)(e^{-ik(\frac{2\pi}{N})})^n 【1式】
X[k]=n=0∑N−1f(t)(e−ik(N2π))n【1式】
x[k]=1N∑n=0N−1X[n](eik(2πN))n【2式】
x[k]=\frac{1}{N}\sum^{N-1}_{n=0}X[n](e^{ik(\frac{2\pi}{N})})^n【2式】
x[k]=N1n=0∑N−1X[n](eik(N2π))n【2式】
对于上面的2式来说,eikn(2πN)e^{ikn(\frac{2\pi}{N})}eikn(N2π)是构成这个式子的基,当k取1时,ekn(2πN)e^{kn(\frac{2\pi}{N})}ekn(N2π)为基频成分,k不为1时,称其为k次谐波分量。因为其周期是NNN,所以无论怎么取,只有N个谐波分量是独立的。
为了方便,我们令WN=e−i(2πN)W_N=e^{-i(\frac{2\pi}{N})}WN=e−i(N2π)
所以上面定义的式子可以写成下面形式
X[k]=∑n=0N−1f(t)Wnk【3式】
X[k]=\sum^{N-1}_{n=0}f(t)W^{nk} 【3式】
X[k]=n=0∑N−1f(t)Wnk【3式】
x[k]=1N∑n=0N−1X[n]W−nk【4式】
x[k]=\frac{1}{N}\sum^{N-1}_{n=0}X[n]W^{-nk}【4式】
x[k]=N1n=0∑N−1X[n]W−nk【4式】
从前面我们已经知道,非周期连续函数傅里叶变换如下
F(ω)=∫−∞+∞f(t)e−iωtdt
F(\omega)=\int ^{+\infty}_{-\infty}f(t)e^{-i\omega t}dt
F(ω)=∫−∞+∞f(t)e−iωtdt
单位冲激函数的傅里叶变换如下
F[δ(t−t0)]=∫−∞+∞δ(t−t0)e−iωtdt=e−iωt0
\begin{array}{ll}
F[\delta(t-t_0)]&=\int ^{+\infty}_{-\infty}\delta(t-t_0)e^{-i\omega t}dt \\
&\\
&=e^{-i\omega t_0}
\end{array}
F[δ(t−t0)]=∫−∞+∞δ(t−t0)e−iωtdt=e−iωt0
假设现在有一个冲激串,如下
S△T(t)=∑n=−∞+∞δ(t−n△T)
S_{\bigtriangleup T}(t)=\sum^{+\infty}_{n=-\infty}\delta(t-n\bigtriangleup T)
S△T(t)=n=−∞∑+∞δ(t−n△T)
这个冲击串表示,每隔△T\bigtriangleup T△T时间,都会采样一样,其函数图像如下
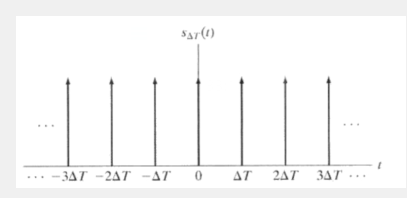 (图像参考《数字图像处理》冈萨雷斯)
(图像参考《数字图像处理》冈萨雷斯)
所谓离散二字,就是要求数据是离散的,而非连续的,我们可以使用一个周期串,对一个信号(函数)进行采样,这样就可以得到一个离散的数据了
现在我们要对上述周期串函数求傅里叶变换,这里的只的傅里叶变换是指广义的傅里叶变换,因为这个函数很明显它是不满足狄利克雷条件的。求法如下
因为S△T(t)S_{\bigtriangleup T}(t)S△T(t)是一个周期函数,所以我们可以把它表示成一个傅里叶级数的形式
S△T(t)=∑n=−∞+∞Cneinωst S_{\bigtriangleup T}(t)=\sum^{+\infty}_{n=-\infty}C_ne^{in\omega_s t} S△T(t)=n=−∞∑+∞Cneinωst
CnC_nCn可以利用下述公式求出
Cn=1△T∫−△T2△T2S△Te−inωst
C_n=\frac{1}{\bigtriangleup T}\int ^{\frac{\bigtriangleup T}{2}}_{-\frac{\bigtriangleup T}{2}}S_{\bigtriangleup T}e^{-in\omega_s t}
Cn=△T1∫−2△T2△TS△Te−inωst
注意,上述积分区间,周期窜只采样了一次。而且是在0点处采样的,所以除了0点,其他点处的函数值都为0
Cn=1△Te0=1△T
C_n=\frac{1}{\bigtriangleup T}e^{0}=\frac{1}{\bigtriangleup T}
Cn=△T1e0=△T1
然后我们可以得到
S△T(t)=∑n=−∞+∞1△Teinωst=1△T∑n=−∞+∞einωst
S_{\bigtriangleup T}(t)=\sum^{+\infty}_{n=-\infty}\frac{1}{\bigtriangleup T}e^{in\omega_s t}=\frac{1}{\bigtriangleup T}\sum^{+\infty}_{n=-\infty}e^{in\omega_s t}
S△T(t)=n=−∞∑+∞△T1einωst=△T1n=−∞∑+∞einωst
然后再对上述式子进行傅里叶变换
F[S△T(t)]=F[∑n=−∞+∞1△Teinωst]dt=∑n=−∞+∞F[1△Teinωst]=1△T∑n=−∞+∞F[einωst]=1△T∑n=−∞+∞δ(ω−nωs)
\begin{array}{ll}
F[S_{\bigtriangleup T}(t)]&=F[\sum^{+\infty}_{n=-\infty}\frac{1}{\bigtriangleup T}e^{in\omega_s t}]dt \\
&\\
&=\sum^{+\infty}_{n=-\infty}F[\frac{1}{\bigtriangleup T}e^{in\omega_s t}]\\
&\\
&=\frac{1}{\bigtriangleup T}\sum^{+\infty}_{n=-\infty}F[e^{in\omega_s t}]
&\\&\\
&=\frac{1}{\bigtriangleup T}\sum^{+\infty}_{n=-\infty}\delta(\omega-n\omega_s)
\end{array}
F[S△T(t)]=F[∑n=−∞+∞△T1einωst]dt=∑n=−∞+∞F[△T1einωst]=△T1∑n=−∞+∞F[einωst]=△T1∑n=−∞+∞δ(ω−nωs)
从上述式子可以看到,当对一个冲激窜进行傅里叶变换之后,其频谱图任然是一个冲激窜,但是其幅度变为了原来的1△T\frac{1}{\bigtriangleup T}△T1。
现在我们来用冲激串,对原始数据进行抽样,公式如下
p(t)=f(t)S△T(t)=∑n=−∞+∞f(t)δ(t−n△T)=f(k△T)
\begin{array}{ll}
p(t)=f(t)S_{\bigtriangleup T}(t)&=\sum^{+\infty}_{n=-\infty}f(t)\delta(t-n\bigtriangleup T)\\
&\\
&=f(k\bigtriangleup T)
\end{array}
p(t)=f(t)S△T(t)=∑n=−∞+∞f(t)δ(t−n△T)=f(k△T)
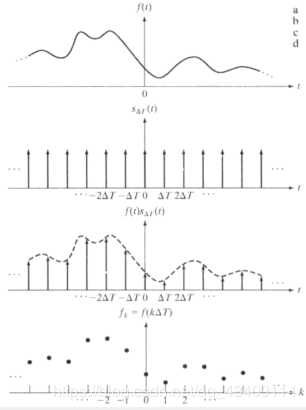
采样完成之后,数据就成离散的了。现在我们考虑对其进行傅里叶变换,因为F[p(t)]F[p(t)]F[p(t)]是一周期连续函数,所以我们只需要在一个周期内采样即可
F[p(t)]=1△T∫0△Tf(t)δ(t−n△T)e−iωtdt=∑n=0M−1f(n△T)e−inω△T=∑n=0M−1fne−inω△T
\begin{array}{ll}
F[p(t)]&=\frac{1}{\bigtriangleup T}\int ^{\bigtriangleup T}_{0}f(t)\delta(t-n\bigtriangleup T)e^{-i\omega t}dt\\
&\\
&=\sum^{M-1}_{n=0}f(n\bigtriangleup T)e^{-in\omega \bigtriangleup T}\\
&\\
&=\sum^{M-1}_{n=0}f_ne^{-in\omega \bigtriangleup T}\\
\end{array}
F[p(t)]=△T1∫0△Tf(t)δ(t−n△T)e−iωtdt=∑n=0M−1f(n△T)e−inω△T=∑n=0M−1fne−inω△T
因为对一个周期进行积分,所以ttt就变成一个周期。假设采集M个点。所以公式变成如下
F(m)=∑n=0M−1fne−inω△T=∑n=0M−1fne−in2π△T△TmM=∑n=0M−1fne−i2πnmM
F(m)=\sum^{M-1}_{n=0}f_ne^{-in\omega \bigtriangleup T}=\sum^{M-1}_{n=0}f_ne^{-in\frac{2\pi}{\bigtriangleup T}\bigtriangleup T}\frac{m}{M}=\sum^{M-1}_{n=0}f_ne^{-i2\pi n\frac{m}{M}}
F(m)=n=0∑M−1fne−inω△T=n=0∑M−1fne−in△T2π△TMm=n=0∑M−1fne−i2πnMm
经过上述变换之后,最终就可以得到离散的傅里叶频谱图
如果我们想用经过离散傅里叶变换之后得到的数据经过反变换得到原始数据的话,可以用傅里叶反变换
f(x)=1M∑m=0M−1F(m)ej2πmxM
f(x)=\frac{1}{M}\sum^{M-1}_{m=0}F(m)e^{j2\pi m\frac{x}{M}}
f(x)=M1m=0∑M−1F(m)ej2πmMx
下面用python实现DFT和IDFT,在此之前还要写一个复数类,支持复数的加法、减法、乘法以即求模运算
复数类
'复数类'
class Complex:
#初始化复数类,第一个参数为实部,第二个参数为虚部
def __init__(self,r,i=0):
self.Re=r
self.Im=i
#重载加法符
def __add__(self, other):
real=self.Re+other.Re
imginary=self.Im+other.Im
return Complex(real,imginary)
#重载减法符
def __sub__(self, other):
real=self.Re-other.Re
imginary=self.Im-other.Im
return Complex(real,imginary)
#重载乘法符
def __mul__(self, other):
real=self.Re*other.Re-self.Im*other.Im
imginary=self.Re*other.Im+self.Im*other.Re
return Complex(real,imginary)
#取模
def mo(self):
return np.sqrt((self.Re**2+self.Im**2))
#得到实部
def getRe(self):
return self.Re
# 得到虚部
def getIm(self):
return self.Im
def __repr__(self):
return self.__str__()
def __str__(self):
if self.Re==0:
return str(round(self.Im,2)) + "i"
if self.Im==0:
return str(round(self.Re,2))
if self.Im>0:
return str(round(self.Re,2))+"+"+str(round(self.Im,2))+"i"
if self.Im < 0:
return str(round(self.Re,2)) +str(round(self.Im,2)) + "i"
另外提一下,DFT和IDFT还可以写成矩阵的形式(参考《信号与系统 下》郑里君)
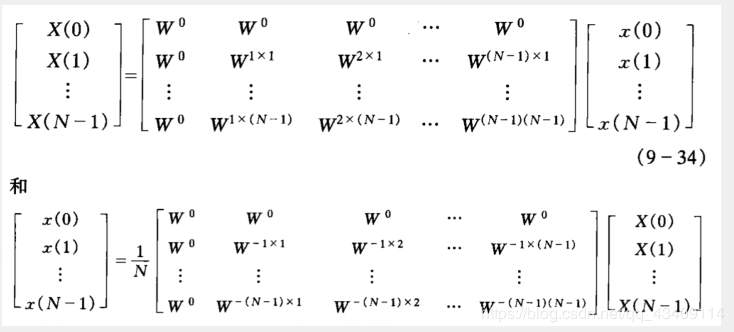
DFT和IDFT
def DFT(fs):
res=np.empty(shape=len(fs),dtype=Complex)
M=len(fs)
for m in range(0,len(fs)):
f_m=Complex(0)
for n in range(0,M):
f_m=f_m+fs[n]*Complex(np.cos(-2.*np.pi*n*m/M),np.sin(-2.*np.pi*n*m/M))
res[m]=f_m
return res
def IDFT(fm):
M=len(fm)
fn=np.empty(shape=M,dtype=Complex)
for n in range(0,M):
fn[n]=Complex(0)
for m in range(0,M):
fn[n]=fn[n]+fm[m]*Complex(np.cos(2*np.pi*n*m/M),np.sin(2*np.pi*n*m/M))
fn[n]=fn[n]*Complex(1/M)
return fn
运行结果

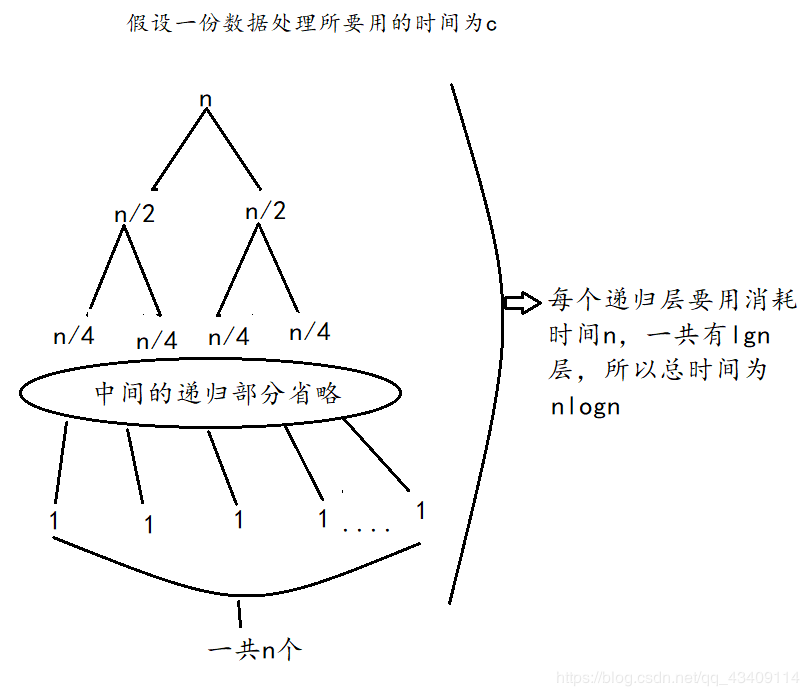
FTT算法,中文名称为快速傅里叶变换,这个算法是DFT的加速版,DFT的时间复杂度是Θ(n2)\Theta(n^2)Θ(n2),而FTT的时间复杂度为Θ(nlgn)\Theta(nlgn)Θ(nlgn),这个速度的提升就相当于从冒泡排序升级到归并排序(这里用归并排序做比较是因为FTT的原理是分治,与归并很像)。
这里总结了《算法导论》中FTT的思想方法,在第三十章,可以自己去看。
在《算法导论》中,作者是通过多项式乘法来逐步引导出快速傅里叶变换,但我觉得还不如直接坦荡的说明其算法思想来的快,然后再做一些应用。
先将DFT的公式进行一下改造,使其看的更清楚一些
F(m)=∑n=0M−1fne−i2πnmM
F(m)=\sum^{M-1}_{n=0}f_ne^{-i2\pi n\frac{m}{M}}
F(m)=n=0∑M−1fne−i2πnMm
我们可以用
ωMm=e−i2πmM
\omega_{M}^m=e^{-i2\pi\frac{m}{M}}\\
ωMm=e−i2πMm
所以,改造之后,DFT公式变为
F(m)=∑n=0M−1fn(ωMm)n
F(m)=\sum^{M-1}_{n=0}f_n(\omega_{M}^m)^n
F(m)=n=0∑M−1fn(ωMm)n
现在假设我们有一个序列fff为[a0,a1,a2,a3,a4,a5,a6,......,an][a_0,a_1,a_2,a_3,a_4,a_5,a_6,......,a_n][a0,a1,a2,a3,a4,a5,a6,......,an],其中n是2的次幂。其中[F0,F1,F2,F3,F4,F5,F6,......Fn][F_0,F_1,F_2,F_3,F_4,F_5,F_6,......F_n][F0,F1,F2,F3,F4,F5,F6,......Fn]为对应的离散傅里叶变换序列
拿出单独拿出一个序列来看
Fk=∑n=0M−1fn(ωMk)n=a0(ωMk)0+a1(ωMk)1+a2(ωMk)2+a3(ωMk)3+.+aM−1(ωMk)M−1
F_k=\sum^{M-1}_{n=0}f_n(\omega_{M}^k)^n=a_0(\omega_{M}^k)^0+a_1(\omega_{M}^k)^1+a_2(\omega_{M}^k)^2+a_3(\omega_{M}^k)^3+.+a_{M-1}(\omega_{M}^k)^{M-1}
Fk=n=0∑M−1fn(ωMk)n=a0(ωMk)0+a1(ωMk)1+a2(ωMk)2+a3(ωMk)3+.+aM−1(ωMk)M−1
对上面的式子,如果我们写程序计算的话,需要一个M次循环,因为一共有M这样的数据要计算,所以一共要计算M2M^2M2次。而FFT就是要优化上面的式子,使其只计算lgMlgMlgM次。FTT的做法大概如下
先将奇数项和偶数项分别提出来
A0=a0(ωMk)0+a2(ωMk)2+a4(ωMk)4+.+aM−2(ωMk)M−2A1=a1(ωMk)1+a3(ωMk)3+a5(ωMk)5+.+aM−1(ωM−1k)M−1
A_0=a_0(\omega_{M}^k)^0+a_2(\omega_{M}^k)^2+a_4(\omega_{M}^k)^4+.+a_{M-2}(\omega_{M}^k)^{M-2}\\
A_1=a_1(\omega_{M}^k)^1+a_3(\omega_{M}^k)^3+a_5(\omega_{M}^k)^5+.+a_{M-1}(\omega_{M-1}^k)^{M-1}
A0=a0(ωMk)0+a2(ωMk)2+a4(ωMk)4+.+aM−2(ωMk)M−2A1=a1(ωMk)1+a3(ωMk)3+a5(ωMk)5+.+aM−1(ωM−1k)M−1
再对A1(奇数项)A_1(奇数项)A1(奇数项)进行一下变换
A1=(ωMk)(a1(ωMk)0+a3(ωMk)2+a5(ωMk)4+.+aM−1(ωMk)M−2)
A_1=(\omega_{M}^k)(a_1(\omega_{M}^k)^0+a_3(\omega_{M}^k)^2+a_5(\omega_{M}^k)^4+.+a_{M-1}(\omega_{M}^k)^{M-2})
A1=(ωMk)(a1(ωMk)0+a3(ωMk)2+a5(ωMk)4+.+aM−1(ωMk)M−2)
所以,最后原来的FkF_kFk就称下面
Fk=A0+ωMkA1
F_k=A_0+\omega_{M}^kA_1
Fk=A0+ωMkA1
由消去引理,可得
A0=a0(ωM2k)0+a2(ωM2k)1+a4(ωM2k)2+.+an(ωM2k)M−22
A_0=a_0(\omega_{\frac{M}{2}}^k)^0+a_2(\omega_{\frac{M}{2}}^k)^1+a_4(\omega_{\frac{M}{2}}^k)^2+.+a_n(\omega_{\frac{M}{2}}^k)^{\frac{M-2}{2}}\\
A0=a0(ω2Mk)0+a2(ω2Mk)1+a4(ω2Mk)2+.+an(ω2Mk)2M−2
A1=(ωMk)(a1(ωM2k)0+a3(ωM2k)1+a5(ωM2k)2+.+aM−2(ωM2k)M−22) A_1=(\omega_{M}^k) (a_1(\omega_{\frac{M}{2}}^k)^0+a_3(\omega_{\frac{M}{2}}^k)^1+a_5(\omega_{\frac{M}{2}}^k)^2+.+a_{M-2}(\omega_{\frac{M}{2}}^k)^{\frac{M-2}{2}}) A1=(ωMk)(a1(ω2Mk)0+a3(ω2Mk)1+a5(ω2Mk)2+.+aM−2(ω2Mk)2M−2)
仔细观察A0A_0A0和A1A_1A1,对于A0A_0A0来说,就相当于对剩下一半偶数部分的序列进行一次DFT,对于A1A_1A1来说就是对剩下一半奇数部分序列进行一次DFT的结果在乘以ωMk\omega^k_MωMk
DFT(fm)=DFT(f偶数部分)+因子∗DFT(f奇数部分)
DFT(f_m)=DFT(f_{偶数部分})+因子*DFT(f_{奇数部分})
DFT(fm)=DFT(f偶数部分)+因子∗DFT(f奇数部分)
整个过程就是把对n个数据的DFT转化成2个对n2\frac{n}{2}2n个数据的DFT
还有一个最重要的步骤,在《算法导论》里没有明确指出。
因为上面部分虽说计算速度加快,但始终只计算了序列中的一个FkF_kFk的DFT,但是仔细观察公式,可以得出下面结论
FK+M2=∑n=0M−1fn(ωMK+M2)n=a0(ωMK+M2)0+a1(ωMK+M2)1+a2(ωMK+M2)2+a3(ωMK+M2)3+.+aM−1(ωMK+M2)M−1
F_{K+\frac{M}{2}}=\sum^{M-1}_{n=0}f_n(\omega_{M}^{K+\frac{M}{2}})^n=a_0(\omega_{M}^{K+\frac{M}{2}})^0+a_1(\omega_{M}^{K+\frac{M}{2}})^1+a_2(\omega_{M}^{K+\frac{M}{2}})^2+a_3(\omega_{M}^{K+\frac{M}{2}})^3+.+a_{M-1}(\omega_{M}^{K+\frac{M}{2}})^{M-1}
FK+2M=n=0∑M−1fn(ωMK+2M)n=a0(ωMK+2M)0+a1(ωMK+2M)1+a2(ωMK+2M)2+a3(ωMK+2M)3+.+aM−1(ωMK+2M)M−1
其中
WMM2=−1
W_M^{\frac{M}{2}}=-1
WM2M=−1
所以
WMK+M2=WMKWMM2=−WMK
W_M^{K+\frac{M}{2}}=W^K_MW_M^{\frac{M}{2}}=-W^K_M
WMK+2M=WMKWM2M=−WMK
所以上面式子通过代换可以变成如下
FK+M2=∑n=0M−1fn(ωMK+M2)n=a0−a1(ωMK)1+a2(ωMK)2−a3(ωMK)3+...−aM−1(ωMK)M−1
F_{K+\frac{M}{2}}=\sum^{M-1}_{n=0}f_n(\omega_{M}^{K+\frac{M}{2}})^n=a_0-a_1(\omega_{M}^{K})^1+a_2(\omega_{M}^{K})^2-a_3(\omega_{M}^{K})^3+...-a_{M-1}(\omega_{M}^{K})^{M-1}
FK+2M=n=0∑M−1fn(ωMK+2M)n=a0−a1(ωMK)1+a2(ωMK)2−a3(ωMK)3+...−aM−1(ωMK)M−1
观察可以发现,偶数列的系数相比较FkF_kFk来说没有改变,而奇数列取负了。
Fk+M2=A0−ωMkA1
F_{k+\frac{M}{2}}=A_0-\omega_{M}^kA_1
Fk+2M=A0−ωMkA1
也就说,只要我们得到其中一个数据的傅里叶变换,通过迭代乘以单位复数根可以很快求出整个序列的离散傅里叶变换。
至于IFFT,即快速傅里叶逆变换与上述过程几乎完全一样,具体改动看代码,懒得叙述
python代码实现如下
def FFT(f):
n=len(f)
if n==1:
return f
w_0=Complex(1)
f_0=f[0::2]
f_1=f[1::2]
y=np.empty(shape=n,dtype=Complex)
y_0=FFT(f_0)
y_1=FFT(f_1)
mid=int(n/2)
for k in range(0,mid):
w= Complex(np.cos(-2.*k*np.pi / n), np.sin(-2.*k*np.pi / n))
y[k]=y_0[k]+w*y_1[k]
y[k+mid] =y_0[k] - w * y_1[k]
return y
IFFT
def IFFT(f):
n=len(f)
if n==1:
return f
w_0=Complex(1)
f_0=f[0::2]
f_1=f[1::2]
y=np.empty(shape=n,dtype=Complex)
y_0=IFFT(f_0)
y_1=IFFT(f_1)
mid=int(n/2)
for k in range(0,mid):
w= Complex(np.cos(2.*k*np.pi / n), np.sin(2.*k*np.pi / n))
y[k]=(y_0[k]+w*y_1[k])/n
y[k+mid] =(y_0[k] - w * y_1[k])/n
return y
运行结果

现在来考虑《算法导论》中,这个FFT用来加速多项式乘法的应用,我觉得《算法导论》中并没有把这个问题完全说清楚。
首先看看普通的多项式乘法是如何进行实现的
def multiplication(self,polynomial): # 多项式的乘法
res=Polynomial(polynomial.degree+self.degree)
for x in range(0,len(self.__coefficients__)):
for y in range(0,len(polynomial.__coefficients__)):
res.__coefficients__[x+y]=res.__coefficients__[x+y]+self.__coefficients__[x]*polynomial.__coefficients__[y]
return res
就是直接套两个循环,简单粗暴,效率低下,时间效率为Θ(n2)\Theta(n^2)Θ(n2)。
多项式乘法,实际上就是两个多项式的系数进行卷积运算。先来看看离散的卷积公式
x(n)∗h(n)=∑i=0∞x(i)h(n−i)
x(n)*h(n)=\sum_{i=0}^{\infty}x(i)h(n-i)
x(n)∗h(n)=i=0∑∞x(i)h(n−i)
再来举一个简单的例子,计算如下多项式乘法
C(x)=(x3+2x2+2x+1)(x3+x2+x+1)
C(x)=(x^3+2x^2+2x+1)(x^3+x^2+x+1)
C(x)=(x3+2x2+2x+1)(x3+x2+x+1)
现在我们令x[n]={1,2,2,1},h[n]={1,1,1,1},x[n]=\{1,2,2,1\},h[n]=\{1,1,1,1\},x[n]={1,2,2,1},h[n]={1,1,1,1},分别代表x3到x0x^3到x_0x3到x0的系数
现在我们来利用卷积,来计算上面多项式乘法的结果,其中C[i]C[i]C[i]代表xix^ixi的系数
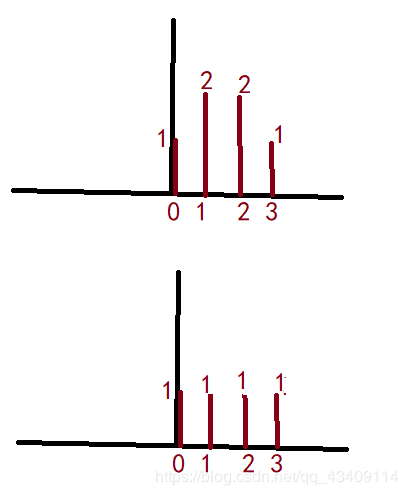
C[0]=∑i=0∞x(i)h(0−i)=1C[0]=\sum_{i=0}^{\infty}x(i)h(0-i)=1C[0]=∑i=0∞x(i)h(0−i)=1,示意图如下
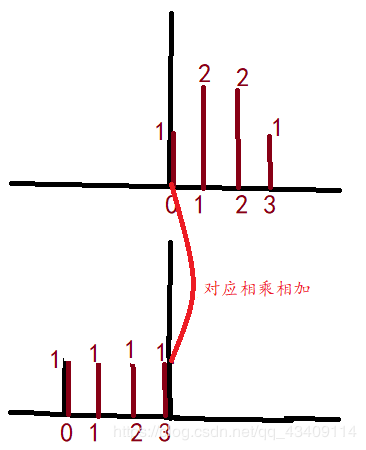
C[1]=∑i=0∞x(i)h(1−i)==1×1+2×1=3C[1]=\sum_{i=0}^{\infty}x(i)h(1-i)==1\times 1+2\times1=3C[1]=∑i=0∞x(i)h(1−i)==1×1+2×1=3,示意图如下
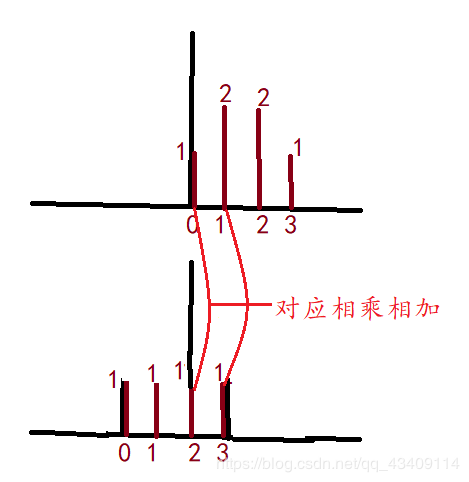
C[2]=∑i=0∞x(i)h(3−i)==1×1+2×1+2×1=5C[2]=\sum_{i=0}^{\infty}x(i)h(3-i)==1\times 1+2\times1+2\times1=5C[2]=∑i=0∞x(i)h(3−i)==1×1+2×1+2×1=5,示意图如下
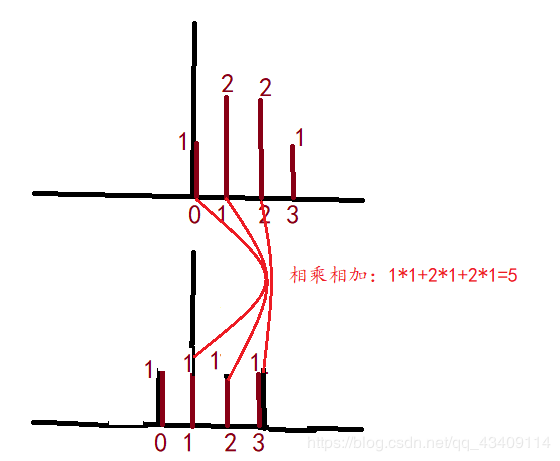
后面的就不继续画图演示了。但是这边又出现了一个问题,如果按照上述卷积公式来计算系数,只能只算到x4x_4x4就无法计算了,所以再进行卷积之前,我们要对x[n]、h[n]x[n]、h[n]x[n]、h[n]进行加倍次数界,用例子来说的话,本来x[n]={1,2,2,1}x[n]=\{1,2,2,1\}x[n]={1,2,2,1},但是加倍次数界之后就变成,x[n]={1,2,2,1,0,0,0,0}x[n]=\{1,2,2,1,0,0,0,0\}x[n]={1,2,2,1,0,0,0,0}。
总言而止,上面的例子就是为了让清楚,实际上多项式的乘法对应的就是多项式系数之间的卷积运算
而根据卷积定理(想要了解的,可以去看《信号与系统》第三章)
x(n)∗h(n)=DFT[x(n)]×DFT[h(n)]
x(n)*h(n)=DFT[x(n)] \times DFT[h(n)]
x(n)∗h(n)=DFT[x(n)]×DFT[h(n)]
也就是,空间域里的卷积运算,对应着频率中的乘积运算。
所以用FFT加速多项式乘法的原理就是,把空间域中复杂的卷积给转换到频率去进行乘法运算,然后再通过逆变换,就可以得到在空间域中的卷积运算的结果了。
def multiplication(x,h):
fft_x=np.fft.fft(x) #对一个方程的系数进行傅里叶变换
fft_h=np.fft.fft(h)#对第二个方程的系数进行傅里叶变换
fft_res=fft_x*fft_h #对两个FFT变换结果进行相乘 (numpy中已经实现了数组相乘)
return np.fft.ifft(fft_res)
上面的算法,执行了2次FFT和一次IFFT,所以一共消耗时间3nlog3nlog3nlog
作者:ReWz