关于2019nCoV新冠肺炎的建模(Ⅲ)—SEIR模型的修正与建立
关于2019nCoV新冠肺炎的建模Ⅲ—SEIR模型的修正与建立引言SEIR建模思路实现程序结果第一次修正的SEIR模型修正思路第一次改进程序实现第二次修正思路实现小结
引言
作者：Matthew.yy
前面笔者尝试从网址中爬取数据，进行分析；在之前做的logistic模型能较好的预测患病人数拐点与峰值。
但是想要模拟出疫情的全过程，logistic是做不到的，于是引入SEIR传染病模型对其进行分析与预测。
这是一个带潜伏期的传染病模型，和没有考虑潜伏期的SI、SIR的优势就显而易见了。
建模思路如下图：
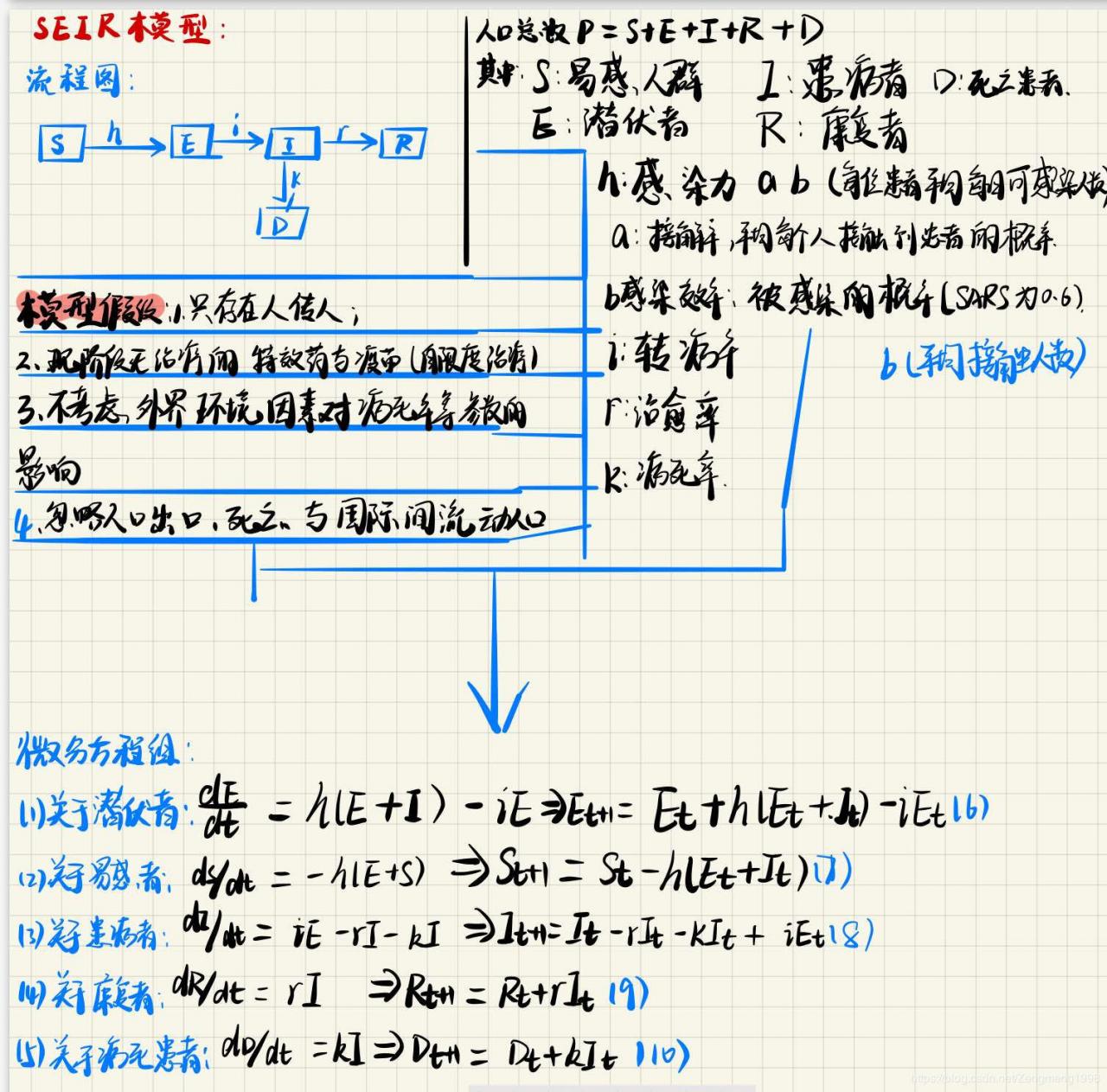
对上述的微分方程求解，不难得到其的差分方程。（字丑勿怪）
参数的选取思路来之笔者的实时疫情数据。
实现工具为matlab
%SEIR模型
clear;clc;
%参数设置
N=1400000000;%人口数
I=1;%传染者
R=0;%康复者
D=0;%死亡患者数量
E=0;%潜伏者
S=N-I;%易感染者
r=1;%接触病患的人数
a=0.125;%潜伏者患病概率
B=0.6;%感染概率
y=0.143;%康复概率
k=0.025373
T=20:1000;
for idx =1:length(T)-1
S(idx+1)=S(idx)-r*B*I(idx)*S(idx)/N;%易感人数迭代
E(idx+1)=E(idx)+r*B*S(idx)*I(idx)/N-a*E(idx)%潜伏者人数迭代
I(idx+1)=I(idx)+a*E(idx)-(y+k)*I(idx);%患病人数迭代
R(idx+1)=R(idx)+y*I(idx);%康复人数迭代
D(idx+1)=D(idx)+k*I(idx);%死亡患者人数迭代
end
plot(T,S,T,E,T,I,T,R,T,D);
grid on;
xlabel('日期');
ylabel('人数');
legend('易感者','潜伏者','传染者','康复者','死亡者');
title('SEIR模型');
plot(T,E,T,I,T,R,T,D);
grid on;
xlabel('日期');
ylabel('人数');
legend('潜伏者','传染者','康复者','死亡者');
title('疫情情况');
结果
实现结果：
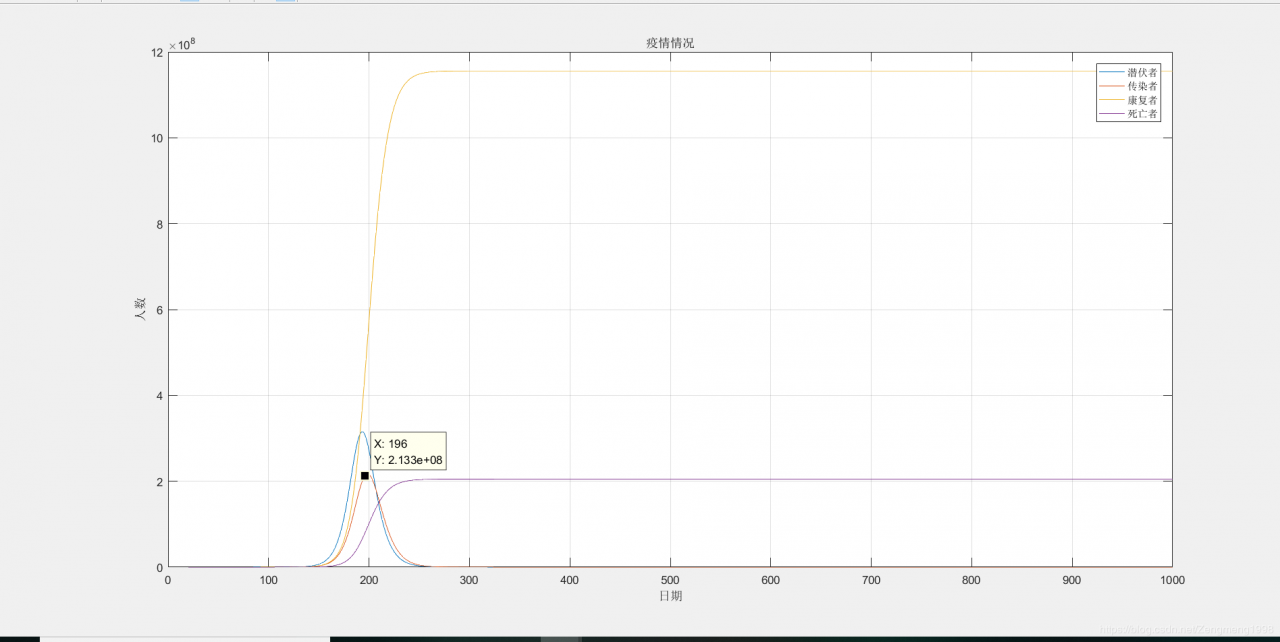结果虽然其将整个过程拟合出来，但是结果并不理想，染病人数的峰值达到了上百万，因此笔者将模型继续进行修正
结合现实，1、武汉疫情12月30日发现第一例疫情患者，1月23日开始封城，于是笔者在第25天时对应减少模型的病者的日接触人数，作为采取隔离措施的体现。
2、将潜伏者与患病者的转染易感者的概率与日接触人数分开为两个参数。
可以得到新的差分迭代式
实现程序参照上文修改，笔者不一一细述最后的实现结果：
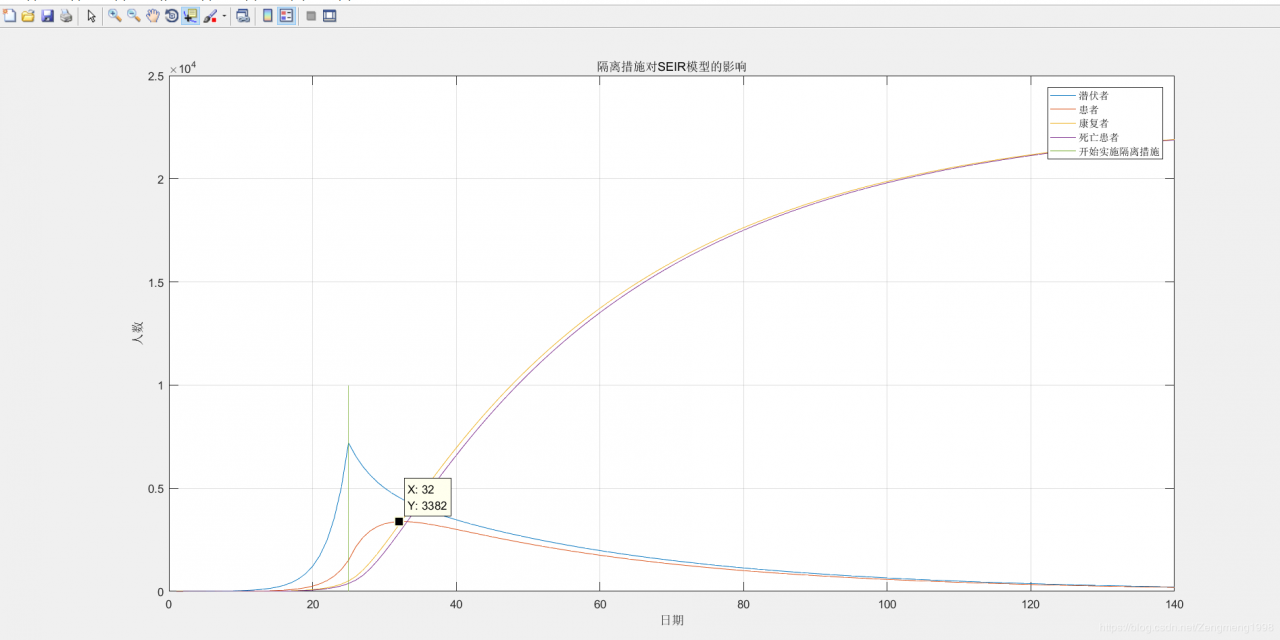
根据图像不难看出，在第25天采取隔离措施后疫情得到很好的的控制，在采取措施的大约10天后疫情进入拐点，得到了控制。
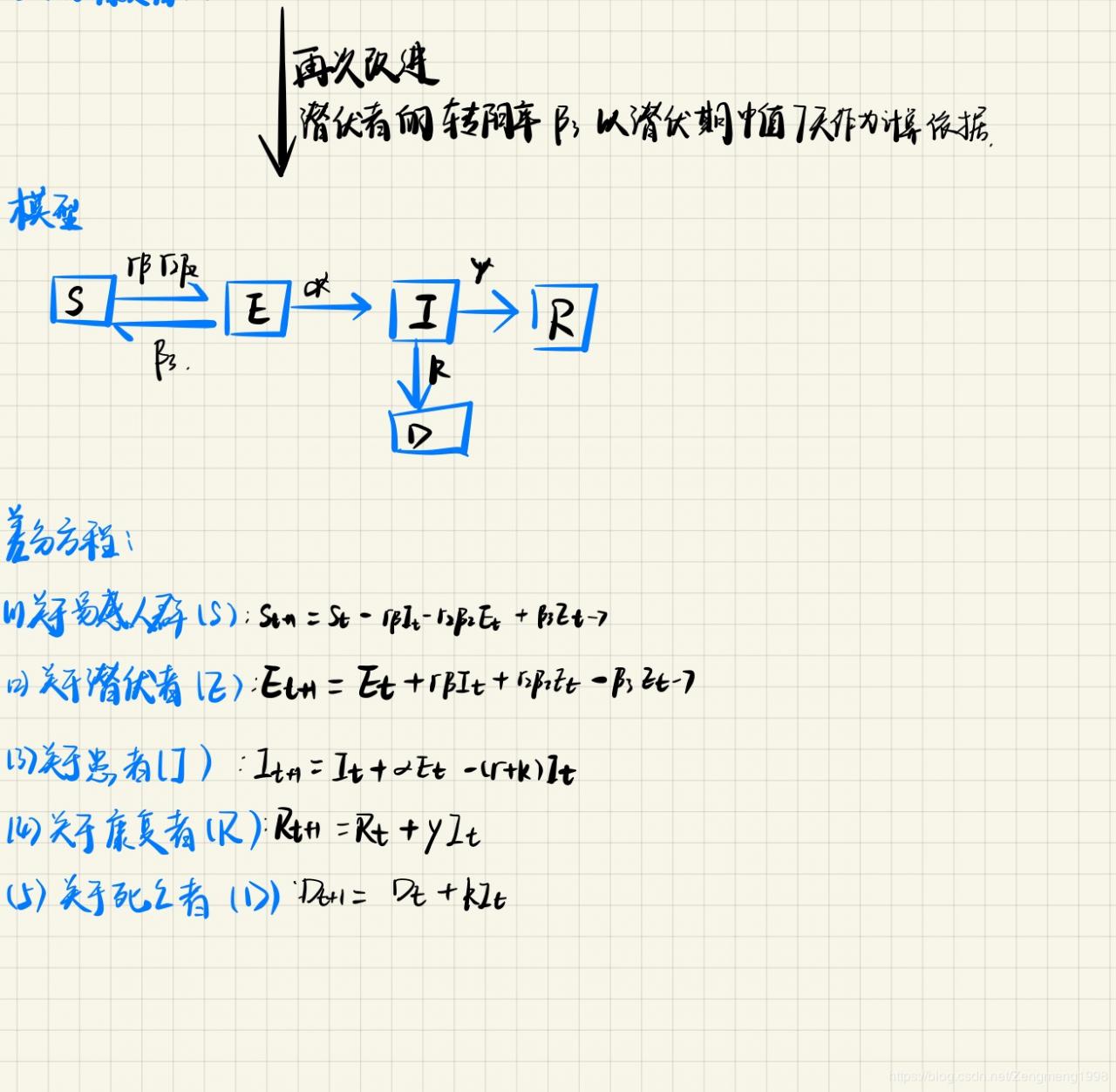
引入潜伏者者转阴率
程序修改参照上文
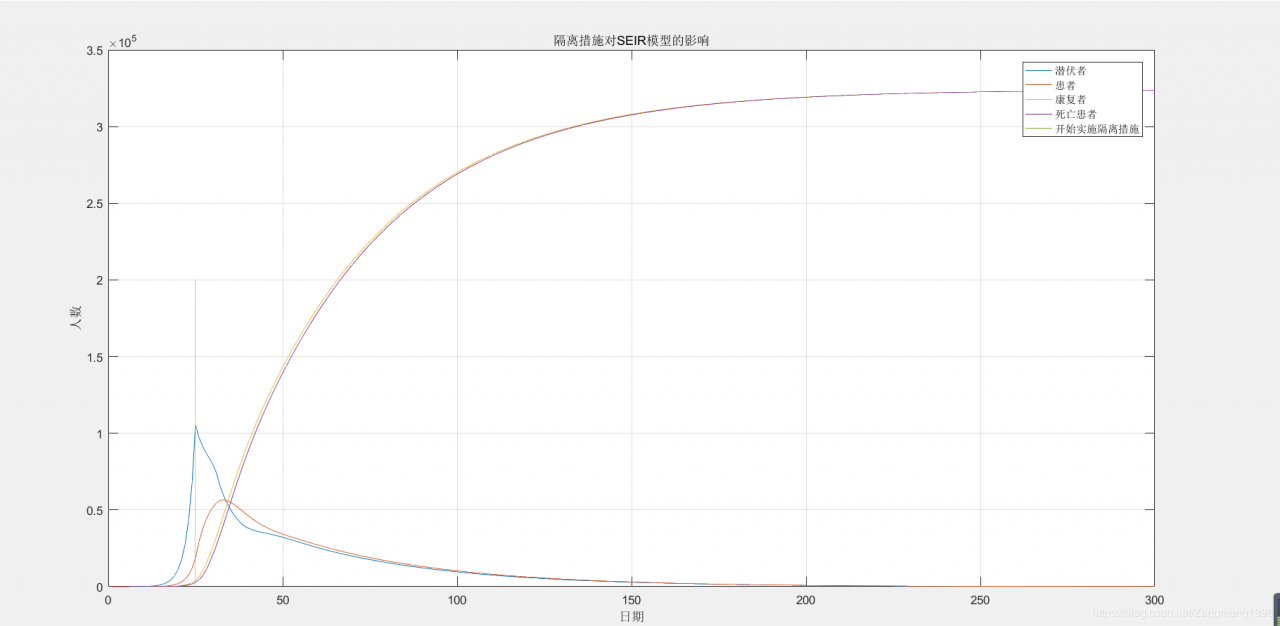
将结果细化
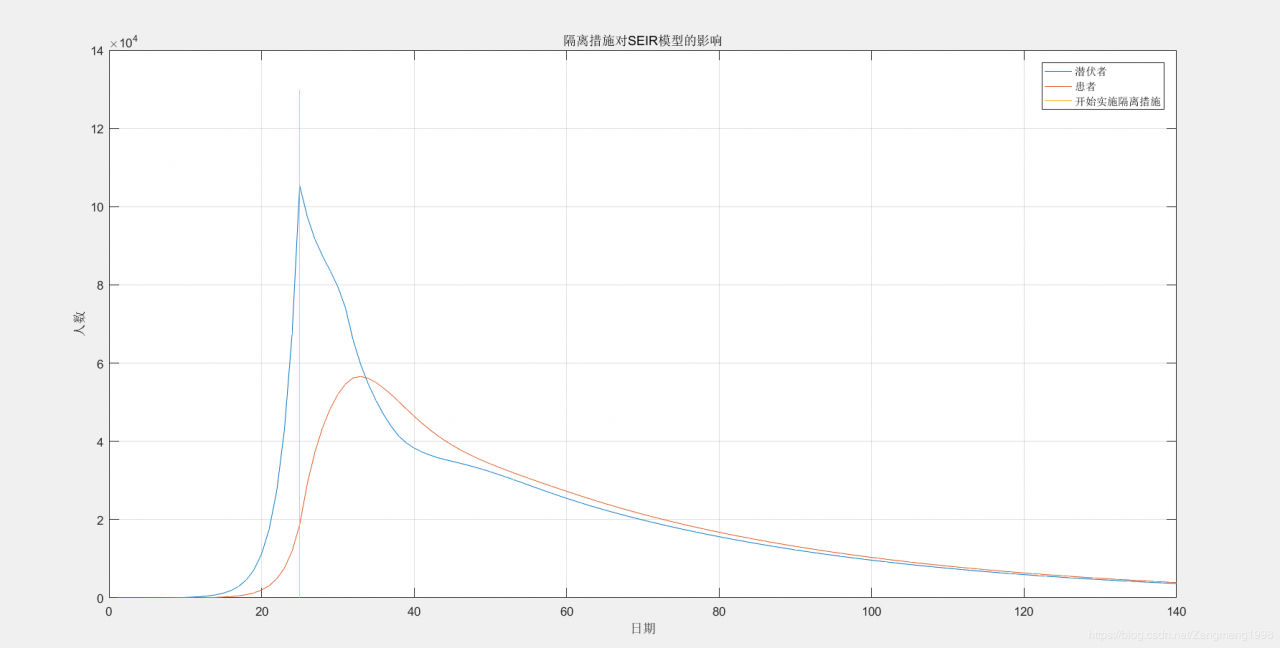
可以看到在疫情发生后的第25天，采取隔离措施措施后，接触过患者的潜伏者明显下降，在之后的约半个月后疫情到达拐点，患病人数峰值约为6万，随后疫情得到控制。
SEIR模型在趋势预测上是要优于logistic模型的，但是由于需要考虑的的参数较多，计算误差要大于logistic模型。
也希望最疫情的控制结果，会比笔者的数学模型还要发展的好！结束的更早。
作者：Matthew.yy
