【计算机组成原理 数字逻辑 Verilog】32位加法器的实现:支持整数的加减运算
本文中所有的Verilog实现部分,均完成了仿真测试,并未进行时序验证以及后续的逻辑综合步骤,后续步骤可能会出现问题,请读者自行完成修改。
1 建模:1位加法器我们先来构建1位加法器,要知道,32位加法器只不过是将32个1位加法器以特定的方式连接起来,真正的核心是1位加法器的设计。
1.1 构建基础模型 1.1.1 一位加法器 1.1.1.1 科技黑箱:外部端口与功能功能:能够实现整数的加减法,这也就意味着
支持正数和负数,支持加法和减法(事实上,a+(-b) = a - b;负数与减法某种程度上来说,是一样的) 能够识别正负数,并且能够做出不同的选择 遇到正数、加法,直接运算 遇到负数、减法 ,转换为补码再运算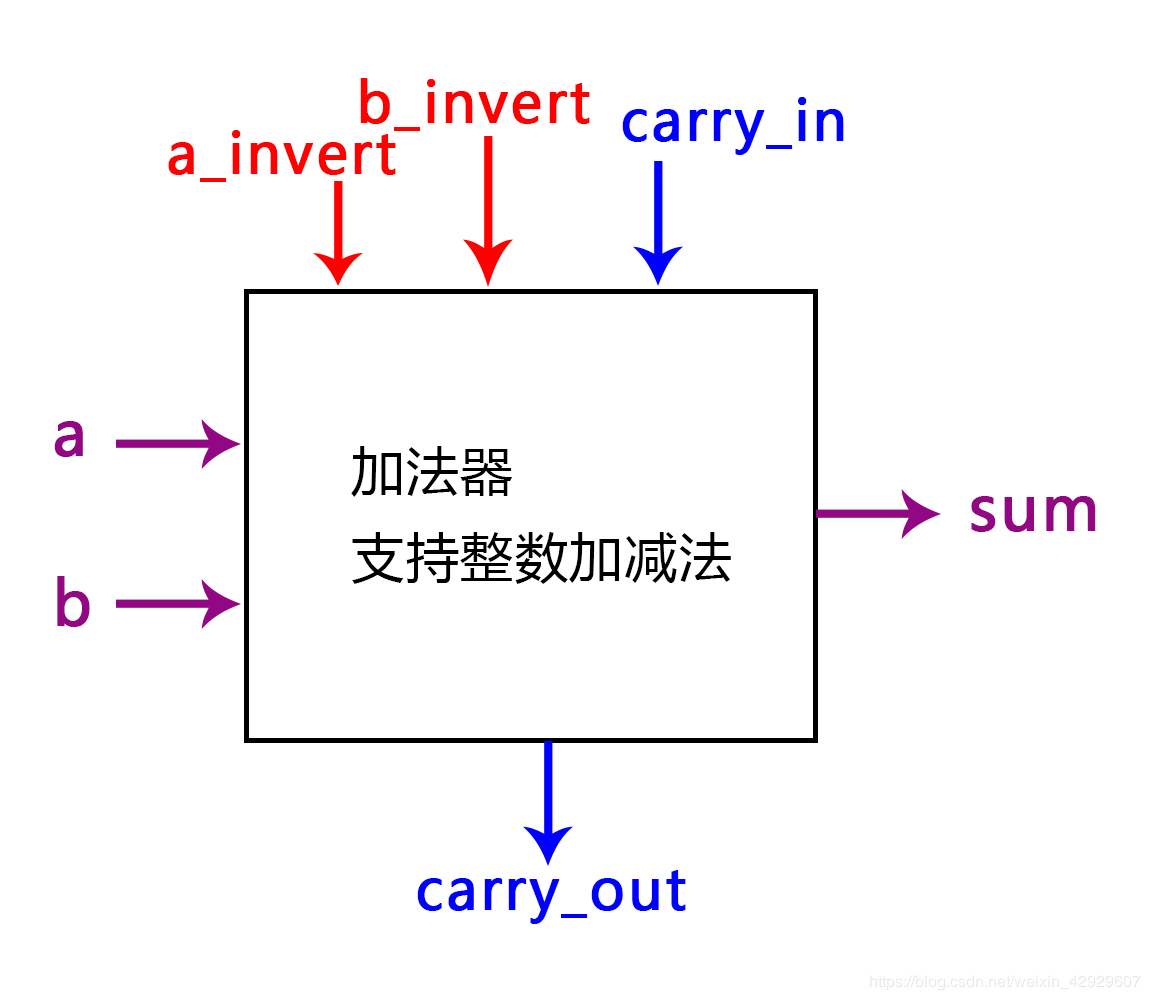
特别注意:对于多个加法器组合的情况,carry_in是来自上一个加法器的carry_out,如果位置是第一个,则要置为0
1.1.1.2 揭秘黑箱:内部结构与模块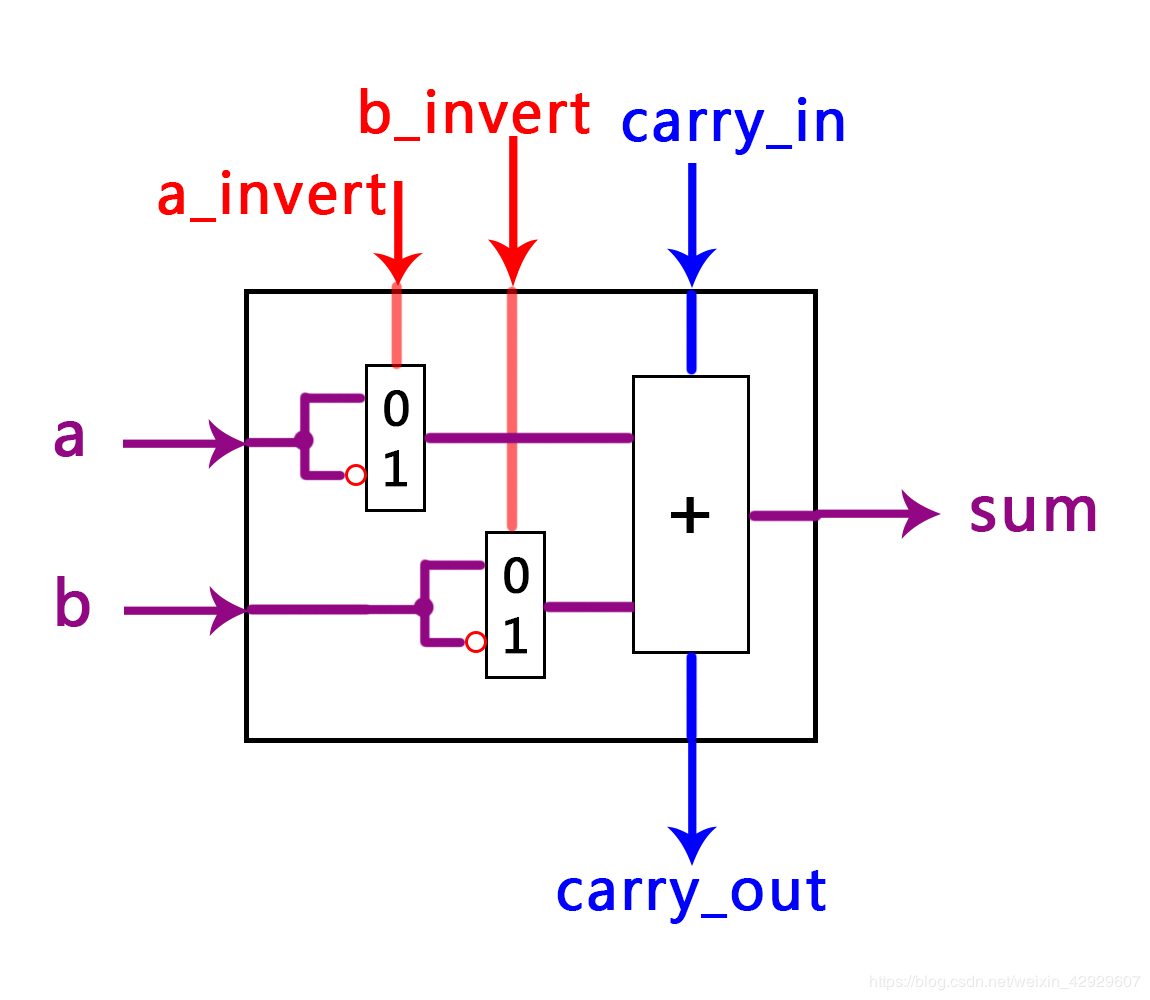
内部线网:不与外部相连的内部线,就是内部线网,在Verilog设计中需要单独加上!
下图图示部分为取反功能选择器,其功能是控制输入的数据是否执行取反操作
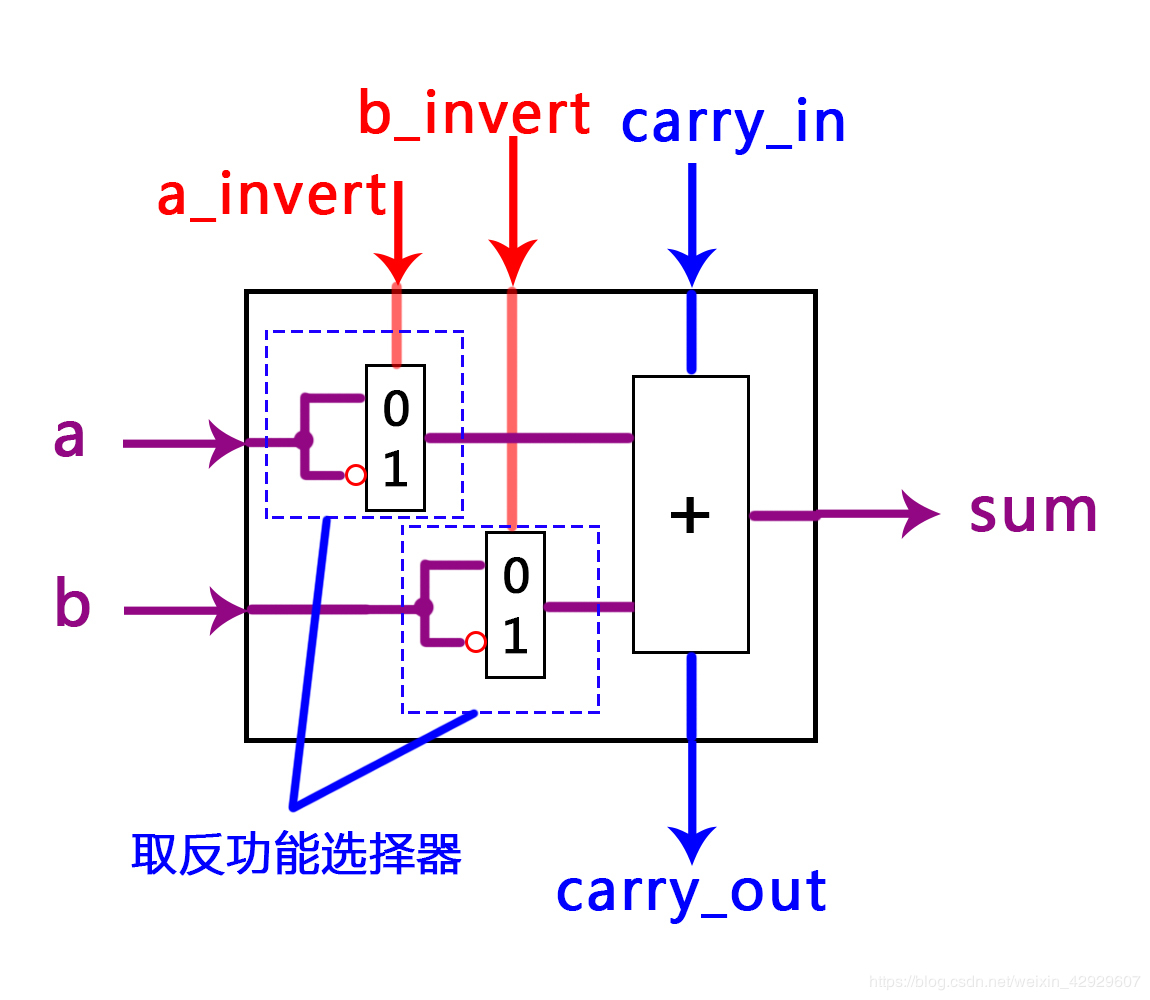
以下是其外部端口:
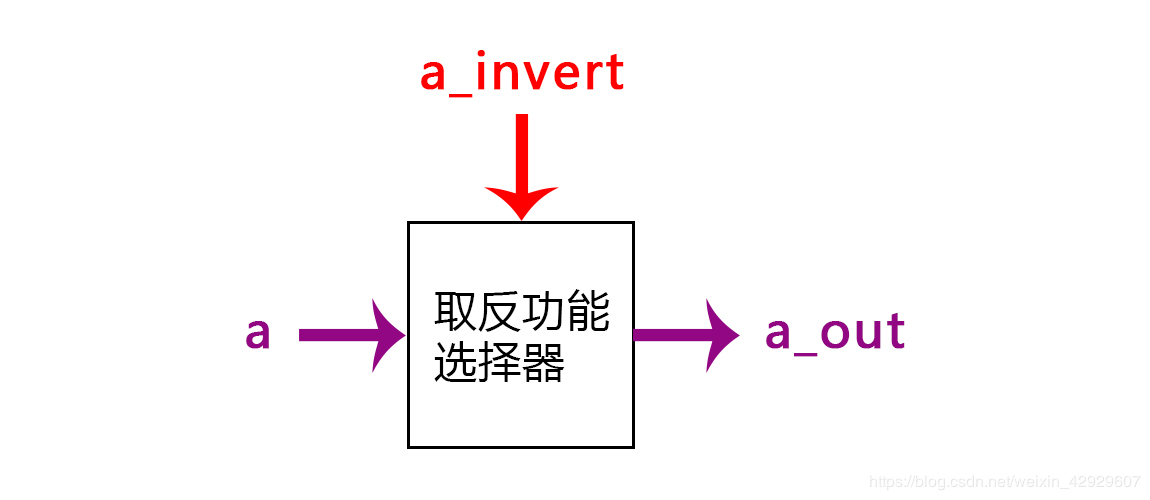
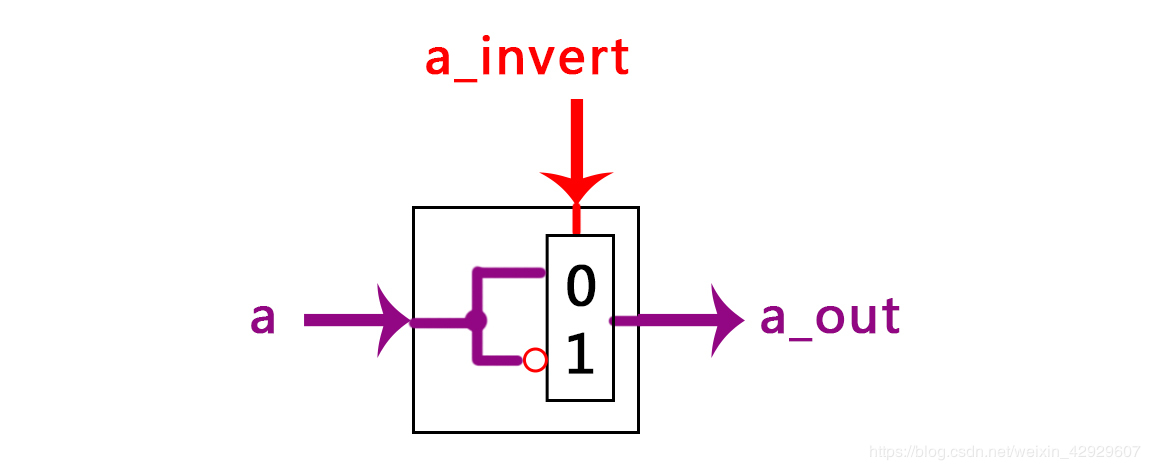
多路选择器的全面讲解参考我的另一篇文章:全面剖析数据选择器
1.1.3 从顶层模块提取低层模块:基础加法器 1.1.3.1 科技黑箱:外部端口与功能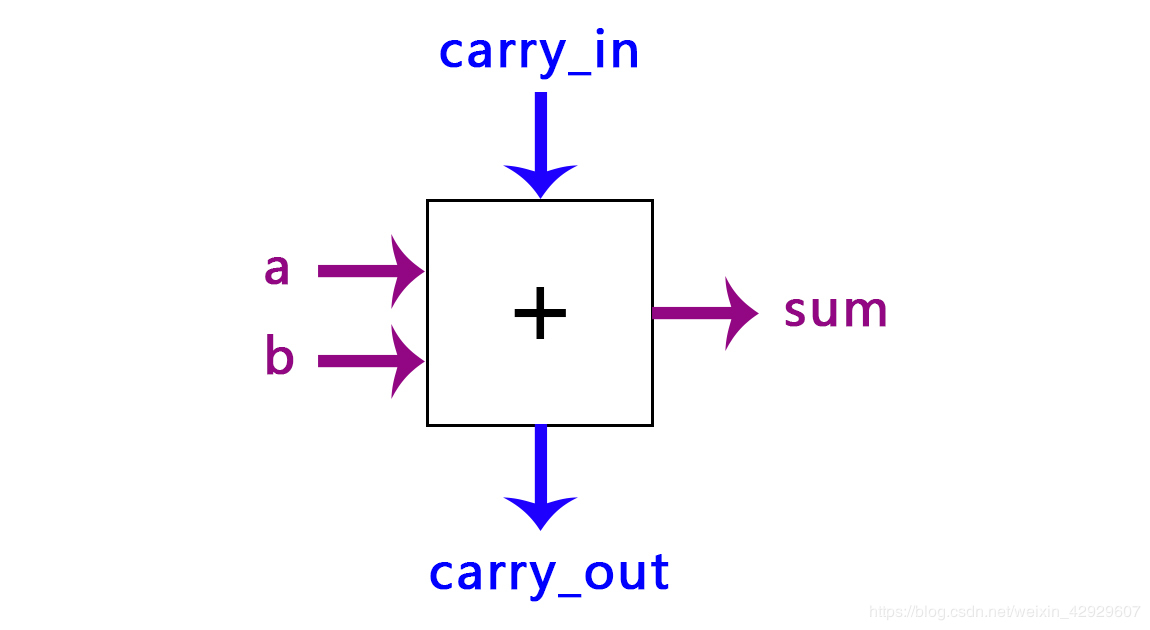
使用数据流建模,两个逻辑表达式就可以,这个部分是数字逻辑必备知识,不再赘述。
1.2 层次建模 1.2.1 32位加法器 1.2.2 1位加法器 2 实现:1位加法器 2.1 取反选择器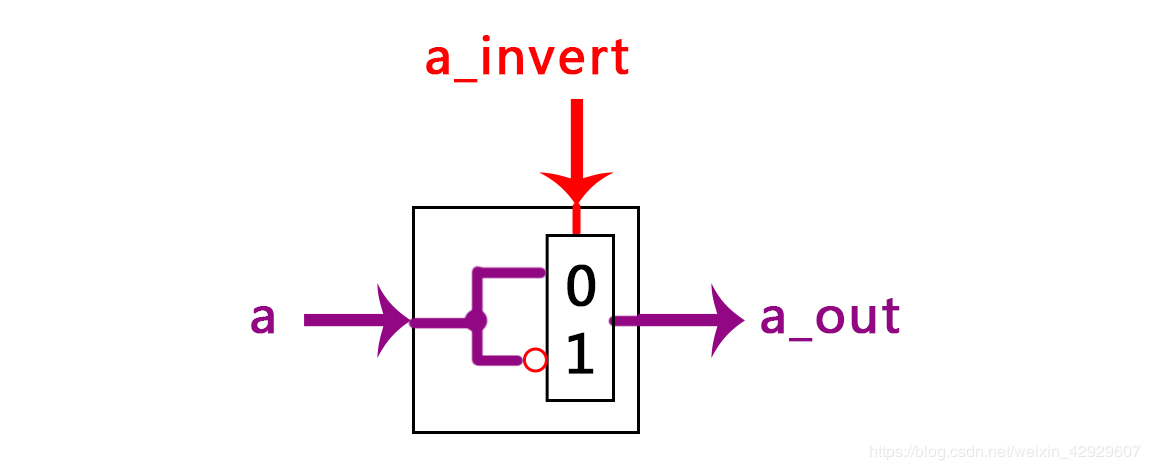
`timescale 1ns / 1ps
// 取反选择器的设计
module date_invert_choose (
input a, // 数据输入
input a_invert, // 使能端
output a_out // 数据输出
);
choose_2to1 CH0 (a,~a,a_invert,a_out); // 调用二选一选择器实例
endmodule
// 二选一选择器
module choose_2to1 (
input d0,d1, // 数据输入
input add, // 地址控制
output out // 数据输出
);
assign out = (~add)&d0 | add&d1;
endmodule
FPGA优化结果如下:
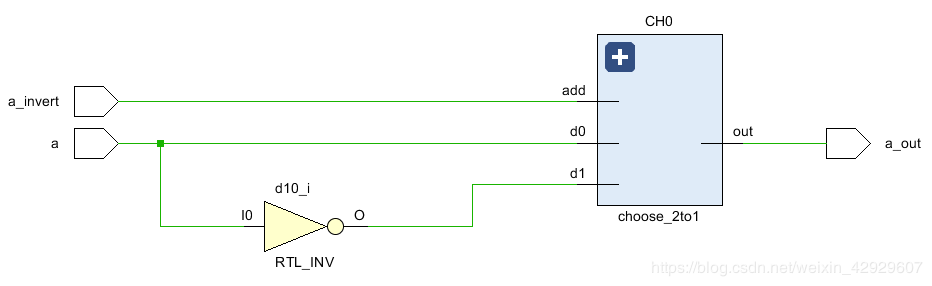
设置激励块有两个口诀:
调用模块,建实例 设置输入,验输出`timescale 1ns / 1ps
module test;
// 设置变量
reg a; // 数据输入
reg a_invert; // 控制输入
wire a_out; // 数据输出
// 调用实例【调用模块建实例】
date_invert_choose DIC0 (a,a_invert,a_out); // 【不要忘了实例名!只有门级描述可以不写】
// 设置信号【设置输入,看输出】
initial
begin
a = 1;
a_invert = 0;
#1 $display("功能%b,直接输出:a_out = %b\n",a_invert,a_out);
a_invert = 1;
#1 $display("功能%b,取反输出:a_out = %b\n",a_invert,a_out);
end
endmodule
2.1.3 功能验证
仿真结果没有问题!
module add_base_1size (
input a,b, // 数据输入
input carry_in, // 进位输入
output carry_out, // 进位输出
output sum // 和
);
assign sum = a ^ b ^ carry_in;
assign carry_out = a&b | (a^b)&carry_in;
endmodule
2.2.2 激励块
请读者自行完成
2.2.3 功能验证经过仿真验证,没有问题。
2.3 1位加法器的实现本节展现的是完整代码,包含2.1和2.2的设计块代码

`timescale 1ns / 1ps
// 取反选择器的设计
module date_invert_choose (
input a, // 数据输入
input a_invert, // 使能端
output a_out // 数据输出
);
choose_2to1 CH0 (a,~a,a_invert,a_out); // 调用二选一选择器实例
endmodule
// 二选一选择器
module choose_2to1 (
input d0,d1, // 数据输入
input add, // 地址控制
output out // 数据输出
);
assign out = (~add)&d0 | add&d1;
endmodule
// 基础加法器
module add_base_1size (
input a,b, // 数据输入
input carry_in, // 进位输入
output carry_out, // 进位输出
output sum // 和
);
assign sum = a ^ b ^ carry_in;
assign carry_out = a&b | (a^b)&carry_in;
endmodule
// 1位加法器的实现
module add_1size (
input a,b, // 数据输入
input a_invert,b_invert, // 求反控制
input carry_in,
output carry_out,
output sum
);
// 内部线网设置
wire a_out,b_out; // 获得经过求反选择器之后的结果
// 调用模块实例
// 求反控制器实例
date_invert_choose DateA (a,a_invert,a_out);
date_invert_choose DateB (b,b_invert,b_out);
// 加法器实例
add_base_1size Add_A_B (a_out,b_out,carry_in,carry_out,sum);
endmodule
2.3.2 激励块&功能验证
module test;
reg a,b; // 注意reg为无符号数
reg a_invert,b_invert;
reg carry_in;
wire carry_out;
wire sum;
add_1size AD0 (a,b,a_invert,b_invert,carry_in,carry_out,sum);
// 设置信号,求 a + (-b)即 a - b
initial
begin
a = 0; b = 0;
a_invert = 0; b_invert = 1; // b取反
carry_in = 1; // b取反加1
#1 $display("a = %b, b = %b, carry_out = %b\na - b = %b\n",a,b,carry_out,sum); // 模拟 a - b
if (sum == 0)
$display("验证成功! 0 - 0 = 0");
end
endmodule
这里的验证我有必要讲解一下,因为有些地方会令人费解。
reg为无符号数,如果直接像reg a = -1这样的语法,存到计算机中是自动以补码形式存储的,那样的话就没有办法验证我们的设计了。要明白的一点是,我们是假定计算机不会自动将负数转换为补码,由我们的设计来实现这个工作,因此,这里我直接手动输入了某个数的原码,再有我们的设计将其转换为补码,这样就完成了验证工作。
我们假定在十进制下,a > 0,-b < 0,我们要求出 a + (-b)的值,并且这台计算机没有将-b存储为补码的功能,我们又知道b的二进制形式就是其补码,它在经过全部按位取反再加1后,会得到-b的补码,因此也就有了激励块中的b = 0;和carry_in = 1;,这是为了验证取反加1功能是否正确。
实际的过程是这样的:a + b取反 + 1 = a + (-b) = a - b,这样就是能够让你明白两件事,负数的补码转换和减法转换为加法它的实际过程是这样的:a = 0,b = 0,故a + b取反 + 1 = 0 + 1 + 1 = 10也就是sum = 0;carry_out = 1;
3 原理讲解:实现整数减法,将负数转换为补码
本小节可以跳过,可以看完第4节再回看。
3.1 计算机进制数与人类进制数的差别计算机进制数指的是
二进制 八进制 十六进制人类进制数指的是
十进制两者差别主要在于,十进制数使用 -来表示负数,而计算机进制数使用补码来表示负数,在其数据本身,就包含了符号,而十进制数据是不包含符号位的,它的符号位是单独存在的。这也是机器数数据符号化的特点。
而人类又习惯于使用十进制,这才有了负数的补码转换方法及其硬件设计逻辑。
在这里重点强调,不要理会原码、反码,这是历史上已经被淘汰的东西,他们跟补码,只是有数学上的联系,以及历史原因。
但是,从十进制数转换为补码这一过程跟原码、反码完全没有关系,很多教材和老师的讲解都是不正确的。
我们只需要记住以下原则:
3.1.1 十进制数转换为补码的原理请注意,这里十进制数的对象为:全体实数,包含整数和小数,他们都适用于补码转换规则,重要的一点区别是在计算机存储上
计算机存储整数,直接使用补码表示 计算机存储小数,使用的是浮点表示,关于这一点请详细阅读浮点运算的知识在这里,我们以十进制整数为例来进行说明
对于正数,这个非常容易,直接使用除基取余法即可,高位需要用0补全例如(假定寄存器为16位):
200D = 0000_0000_1100_1000B 对于负数,需要遵循这样的规则:全部取反再加1
例如 -2D:
(1)先表示出2D = 0000_0000_0000_0010B
(2)再全部取反,1111_1111_1111_1101B
(3)再加1,1111_1111_1111_1110B
(4)这样得到的结果就是 -2D的补码
需要注意的是,此时如果高位有空余,需要补上1,而不是0
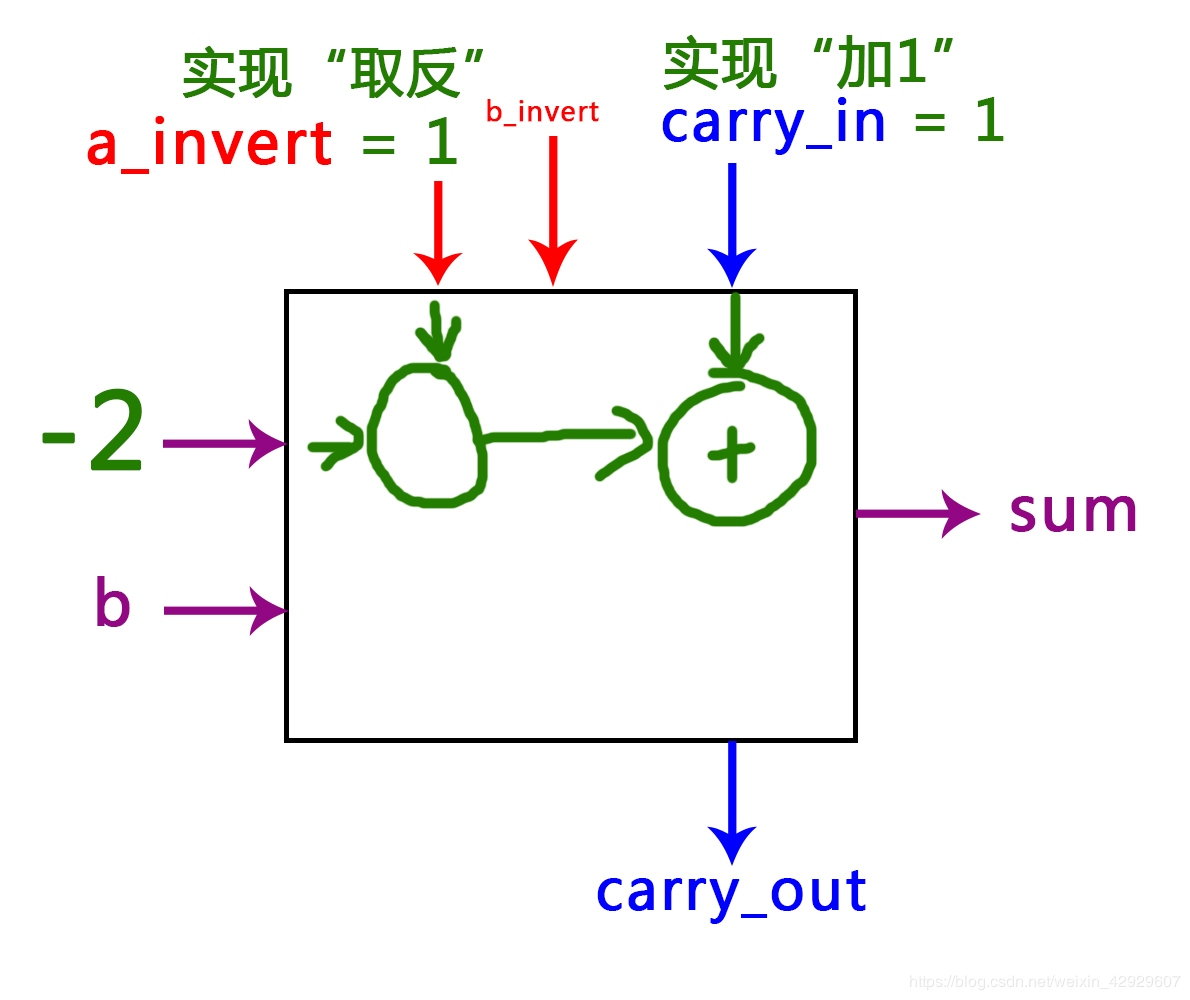
其中,我之前提到的取反功能选择器,就是完成了取反操作,但是还有加1操作呢?我们继续看下一小节!
3.2 进位输入信号carry_in的作用我在1.1.1.1节提到过,carry_这个信号,初始需要置为0,加法器单独存在一个的时候,它是不太重要的。
只有多个加法器连在一起(串行进位,第3节会提及)的时候,上一级的carry_in与下一级的carry_out连接起来,才能发挥作用。
但是,如果初始将carry_in置为1,就能够发挥它的作用了,它在补码转换过程,起到了加1的作用。
无论输入的数据是1位还是32位,加1只需要在最低位加1,也就是只需要把单独存在的,不与carry_out连接的caryy_in置为1,就能实现加1操作。
十进制的2:0000 0000 0000 0010
先取反: 1111 1111 1111 1101
再加1: + 1
————————————————————————
1111 1111 1111 1110
其中:取反操作使用取反选择器完成
加1操作只需将carry_in置为1
这样一来,取反选择器与carry_in = 1紧密合作,就完成了十进制数到补码的转换,也就实现了整数的加减法。
备注:如果这个部分看不懂,请看完第3节再回看此节。
至此,我想你能够理解实现整数减法的硬件设计原理了。
思考点:
这里留一个问题给读者思考,试想,如果采用大多数老师讲解的原码、反码和补码的原则去转换补码,硬件设计会是怎样的?
这里我直接给你结果分析,具体设计不再讲解,自行完成。
显然,按照这样的方式,设计会非常复杂,而且没有必要,既违背了硬件设计简单性原则,也增加了数学运算的复杂度
一般老师讲解的原码、反码和补码的转换方式是
先求原码,再求反码,再求补码我教你的是
全部取反再加1这二者是区别就是
前者教你 1 + 10 - 9 = 2 后者教你: 1 + 1 = 2对比之下,哪个更加简洁不言而喻,事实上,这些都是人为规定,怎么计算都可以,在数学上都说的通,但是要考虑硬件简单性原则,后者显然更加占优势。
假定a,b均为非负整数,则:
a - b = a + ( b取反 + 1 )
但是事实的情况往往会更加复杂,比如:-a - b又如何处理?
目前从原理上能够实现减法,但这远远不够,还需要根据实际需求进一步改进,这就涉及到了将其添加到MIPS指令上,这个以后再说。
3 建模:32位加法器这里采用串行进位方式进行连接,并非并行进位(超前进位)。
关于基础加法器的超前进位实现,参照我的文章:全面剖析:加法器——从1位到4位,从一般加法(串行进位)到快速加法(并行进位/超前进位)【此处链接待完善】
3.1 科技黑箱:外部端口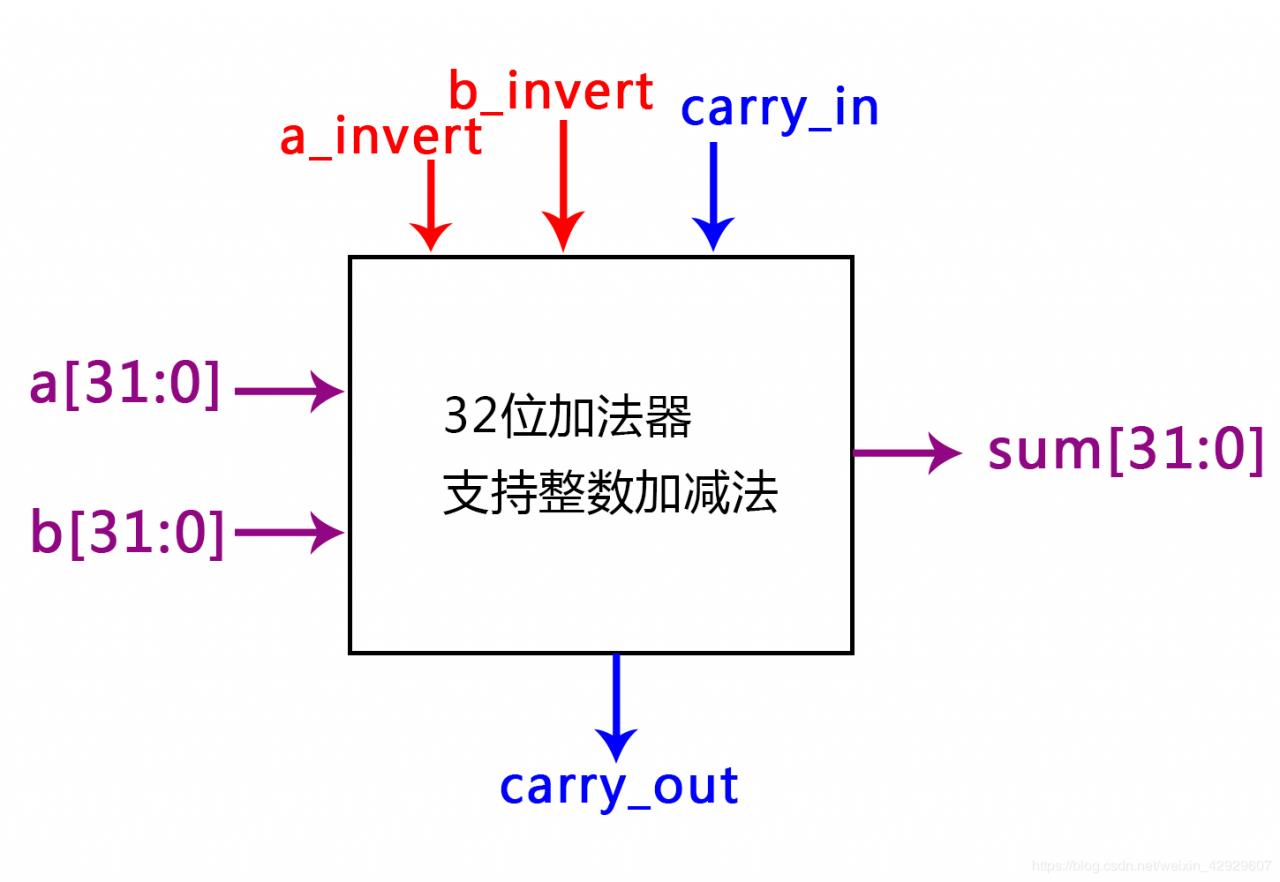
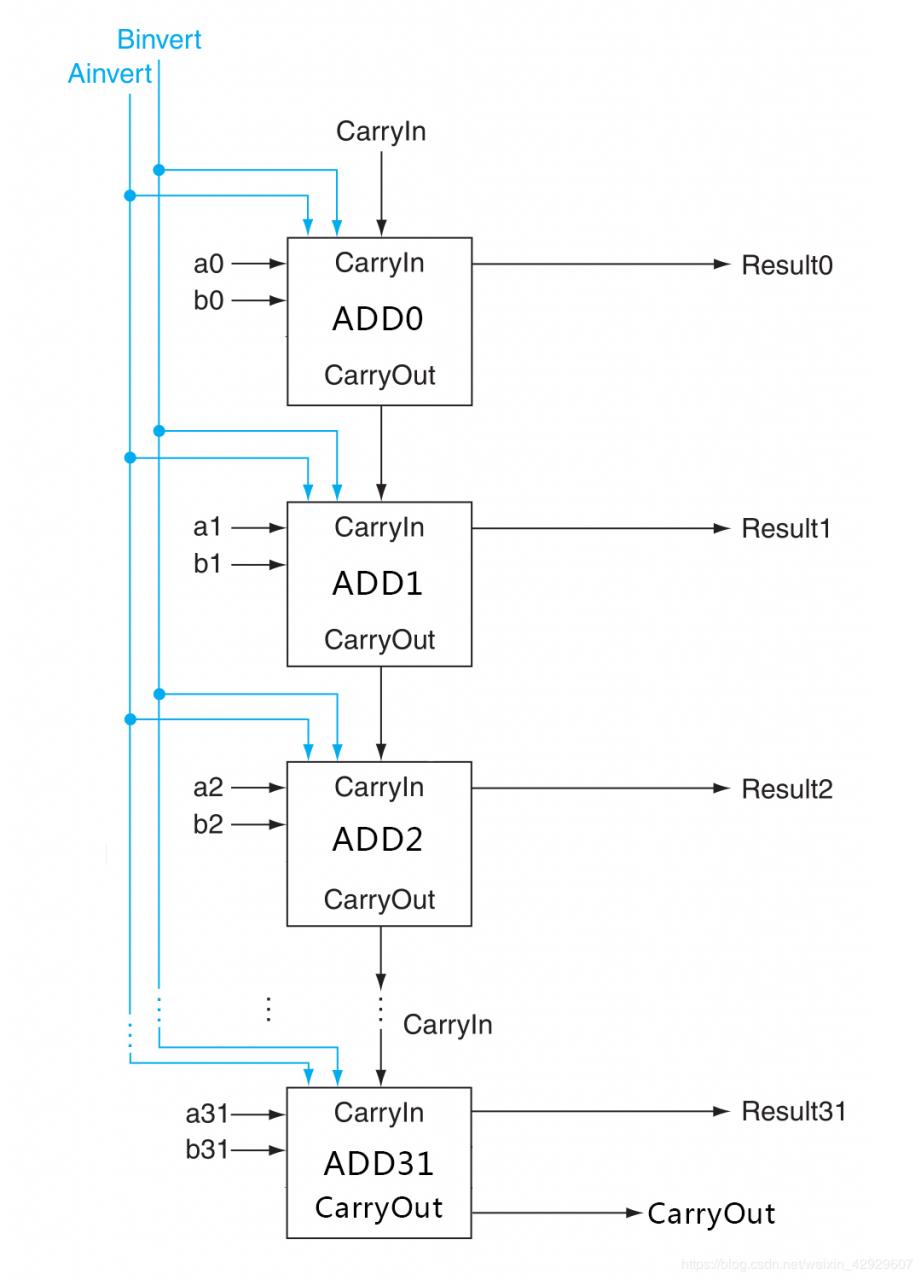

此处直接使用前面设计好的1位加法器,再次强调,此处为串行进位
module add_32sizes (
input [31:0] a,b,
input a_invert,b_invert,
input carry_in,
output carry_out,
output [31:0] sum
);
// 设置内部线网
wire carry_out_in [30:0]; // 内部串行进位传递
// 调用模块实例
add_1size ADD0 (a[0],b[0],a_invert,b_invert,carry_in,carry_out_in[0],sum[0]);
add_1size ADD1 (a[1],b[1],a_invert,b_invert,carry_out_in[0],carry_out_in[1],sum[1]);
add_1size ADD2 (a[2],b[2],a_invert,b_invert,carry_out_in[1],carry_out_in[2],sum[2]);
add_1size ADD3 (a[3],b[3],a_invert,b_invert,carry_out_in[2],carry_out_in[3],sum[3]);
add_1size ADD4 (a[4],b[4],a_invert,b_invert,carry_out_in[3],carry_out_in[4],sum[4]);
add_1size ADD5 (a[5],b[5],a_invert,b_invert,carry_out_in[4],carry_out_in[5],sum[5]);
add_1size ADD6 (a[6],b[6],a_invert,b_invert,carry_out_in[5],carry_out_in[6],sum[6]);
add_1size ADD7 (a[7],b[7],a_invert,b_invert,carry_out_in[6],carry_out_in[7],sum[7]);
add_1size ADD8 (a[8],b[8],a_invert,b_invert,carry_out_in[7],carry_out_in[8],sum[8]);
add_1size ADD9 (a[9],b[9],a_invert,b_invert,carry_out_in[8],carry_out_in[9],sum[9]);
add_1size ADD10 (a[10],b[10],a_invert,b_invert,carry_out_in[9],carry_out_in[10],sum[10]);
add_1size ADD11 (a[11],b[11],a_invert,b_invert,carry_out_in[10],carry_out_in[11],sum[11]);
add_1size ADD12 (a[12],b[12],a_invert,b_invert,carry_out_in[11],carry_out_in[12],sum[12]);
add_1size ADD13 (a[13],b[13],a_invert,b_invert,carry_out_in[12],carry_out_in[13],sum[13]);
add_1size ADD14 (a[14],b[14],a_invert,b_invert,carry_out_in[13],carry_out_in[14],sum[14]);
add_1size ADD15 (a[15],b[15],a_invert,b_invert,carry_out_in[14],carry_out_in[15],sum[15]);
add_1size ADD16 (a[16],b[16],a_invert,b_invert,carry_out_in[15],carry_out_in[16],sum[16]);
add_1size ADD17 (a[17],b[17],a_invert,b_invert,carry_out_in[16],carry_out_in[17],sum[17]);
add_1size ADD18 (a[18],b[18],a_invert,b_invert,carry_out_in[17],carry_out_in[18],sum[18]);
add_1size ADD19 (a[19],b[19],a_invert,b_invert,carry_out_in[18],carry_out_in[19],sum[19]);
add_1size ADD20 (a[20],b[20],a_invert,b_invert,carry_out_in[19],carry_out_in[20],sum[20]);
add_1size ADD21 (a[21],b[21],a_invert,b_invert,carry_out_in[20],carry_out_in[21],sum[21]);
add_1size ADD22 (a[22],b[22],a_invert,b_invert,carry_out_in[21],carry_out_in[22],sum[22]);
add_1size ADD23 (a[23],b[23],a_invert,b_invert,carry_out_in[22],carry_out_in[23],sum[23]);
add_1size ADD24 (a[24],b[24],a_invert,b_invert,carry_out_in[23],carry_out_in[24],sum[24]);
add_1size ADD25 (a[25],b[25],a_invert,b_invert,carry_out_in[24],carry_out_in[25],sum[25]);
add_1size ADD26 (a[26],b[26],a_invert,b_invert,carry_out_in[25],carry_out_in[26],sum[26]);
add_1size ADD27 (a[27],b[27],a_invert,b_invert,carry_out_in[26],carry_out_in[27],sum[27]);
add_1size ADD28 (a[28],b[28],a_invert,b_invert,carry_out_in[27],carry_out_in[28],sum[28]);
add_1size ADD29 (a[29],b[29],a_invert,b_invert,carry_out_in[28],carry_out_in[29],sum[29]);
add_1size ADD30 (a[30],b[30],a_invert,b_invert,carry_out_in[29],carry_out_in[30],sum[30]);
add_1size ADD31 (a[31],b[31],a_invert,b_invert,carry_out_in[30],carry_out,sum[31]);
endmodule
4.2 激励块
注意,因为在Verilog中,reg自动以二进制补码形式存储,所以此处验证负数的时候,我们假定计算机没有以补码存储这一功能,我们假定b = -5,并且手动设置b的值,将b的值设置为5的补码,5的补码就是其二进制表示0101B,以此来验证5的补码经过全部取反加1后,是否变成了-5的补码,从而验证了设计的正确性。
如果你没有看懂,那么请看完第6节的补充链接,再回顾此内容。
module test;
reg [31:0] a,b; // 注意reg为无符号数
reg a_invert,b_invert;
integer carry_in;
wire carry_out;
wire [31:0] sum;
add_32sizes AD0 (a,b,a_invert,b_invert,carry_in,carry_out,sum);
// 设置信号,假设b = -5;a = 8;求a + b
initial
begin
a = 4'b1000; // 8的补码
b = 4'b0101; // reg为无符号数,自动把-5存为补码,无法验证结果,因此使用 |-5| = 5 的补码
a_invert = 0; b_invert = 1; // b取反
carry_in = 1; // b取反加1
#1 $display("a = %d, b = -%d\na + b = %d\n",a,b,sum); // 模拟 a - b
if(sum == 3)
$display("验证成功! 8 + (- 5) = 3");
end
endmodule
4.2.1 报错解决方案
对于这样的错误:[XSIM 43-3238] Failed to link the design.
通常情况下,是因为激励块与设计块的连接出了问题,可能是
模块调用错误 模块忘记实例化 模块接口连接错误可以按照这个思路依次排查
4.3 仿真验证
前面说了那么多,其实,真正硬件编程的时候没有那么麻烦,强大的EDA工具让我们能够只需要描述其行为,就能完成设计,这是抽象层次足够高的设计,让我们来看一下。
这里你可能想要摔电脑了,什么????我做了这么半天,实际上只需要几行??那你写了这么多有啥用!!
冷静一下,仔细想一下,你是不是在之前的操作中,对于加法器已经非常熟悉了?如果你认真做了,我想应该是的,这就是Learning by doing,在做中学,能够快速掌握知识,加深对于知识的理解程度,这一点是很必要的,因此你必须花时间来完成它。
5.1 设计块module add_32bits(
input [31:0] a,b,
input ADDctl, // 控制端,用于识别加减法 0代表加法,1代表减法
output reg [31:0] result
);
always @(a,b,ADDctl)
begin
case(ADDctl)
0: result = a + b;
1: result = a - b;
endcase
end
endmodule
5.2 激励块
module test;
// reg signed [31:0] a,b;
integer a,b;
reg ADDctl;
wire signed [31:0] result;
add_32bits ADD_0 (a,b,ADDctl,result);
initial
begin
// 测试加法
a = -1; b = 20;
ADDctl = 0;
#1 $display("%d + %d = %d",a,b,result);
#1
// 测试减法 【1-20= 溢出值,因为不识别补码!???怎么办】
a = -10; b = 28;
ADDctl = 1;
#1 $display("%d - %d = %d",a,b,result);
end
endmodule
5.3 结果验证

%d形式输出的时候,并不会显示负数,而是显示一个超大的正数,如何解决?
如何正确显示激励块输入的负数,输入端口的reg类型,可否使用integer类型?
以上问题,看完下一小结的扩展链接,你就能得知答案。
6 由行为级描述掌握几大重要思想设计的思想有
分治思想 归一思想 实战验证思维 查阅资料的能力我单独写了一篇文章,以阐述一些重要的理论和思想。请看:待完善
7 待求解决方案的错误[XSIM 43-3345] Unable to remove previous simulation file xsim.dir/test_behav/xsimk.exe. Please check if you have another instance of this simulation running on your system, terminate it and then recompile your design. System Error Message: boost::filesystem::status: 拒绝访问。: "xsim.dir/test_behav/xsimk.exe".
[XSIM 43-3238] Failed to link the design.
我不知道为什么会拒绝访问,并且此状态下,系统不能删除文件,唯一的办法就是重新建立一个文件,并且将设计块和激励块copy过去。
问题待解决中!如有读者知道解决方案,欢迎私聊我~
作者:姜海天—计算机科学与技术专业