【学习计算机组成原理】补码的乘运算

Jessica ·

更新时间:2024-11-10

· 684 次阅读

文章目录补码一位乘运算补码两位乘运算
如果看了原码的乘运算，这篇更容易理解。 补码一位乘运算

假设：
[X]补=xn-1xn-2……x1x0
[Y]补=yn-1yn-2……y1y0

已知补码的性质：X=−xn−1×2n−1+xn−2×2n−2+……+x1×21+x0×20X=-x_{n-1}\times2^{n-1}+x_{n-2}\times2^{n-2}+……+x_{1}\times2^{1}+x_{0}\times2^{0}X=−xn−1×2n−1+xn−2×2n−2+……+x1×21+x0×20

令n=32则：
Y=−y31×231+y30×230+……+y1×21+y0×20Y=-y_{31}\times2^{31}+y_{30}\times2^{30}+……+y_{1}\times2^{1}+y_{0}\times2^{0}Y=−y31×231+y30×230+……+y1×21+y0×20
Y=−y31×231+(y30×231−y30×230)+……+(y1×22−y1×21)+(y0×21−y0×20)Y=-y_{31}\times2^{31}+(y_{30}\times2^{31}-y_{30}\times2^{30})+……+(y_{1}\times2^{2}-y_{1}\times2^{1})+(y_{0}\times2^{1}-y_{0}\times2^{0})Y=−y31×231+(y30×231−y30×230)+……+(y1×22−y1×21)+(y0×21−y0×20)
Y=(y30−y31)×231+(y29−y30)×230+……+(y0−y1)×21+(y−1−y0)×20Y=(y_{30}-y_{31})\times2^{31}+(y_{29}-y_{30})\times2^{30}+……+(y_{0}-y_{1})\times2^{1}+(y_{-1}-y_{0})\times2^{0}Y=(y30−y31)×231+(y29−y30)×230+……+(y0−y1)×21+(y−1−y0)×20
这里y-1=0时等式成立
为了便于处理，我们对Y乘2-32，这样小数点位于最前面。
2−32×[X×Y]补=X×(y30−y31)×2−1+X×(y29−y30)×2−2+……+X×(y−1−y0)×2−322^{-32}\times[X\times Y]_{补}=X\times(y_{30}-y_{31})\times2^{-1}+X\times(y_{29}-y_{30})\times2^{-2}+……+X\times(y_{-1}-y_{0})\times2^{-32}2−32×[X×Y]补=X×(y30−y31)×2−1+X×(y29−y30)×2−2+……+X×(y−1−y0)×2−32
2−32×[X×Y]补=2−1×(X×(y30−y31)+2−1×(X×(y29−y30)+……+2−1×(X×(y−1−y0))))2^{-32}\times[X\times Y]_{补}=2^{-1}\times(X\times(y_{30}-y_{31})+2^{-1}\times(X\times(y_{29}-y{30})+……+2^{-1}\times(X\times(y_{-1}-y_{0}))))2−32×[X×Y]补=2−1×(X×(y30−y31)+2−1×(X×(y29−y30)+……+2−1×(X×(y−1−y0))))
我们可以看到等式中存在y31y_{31}y31，表明补码的符号位也参加运算。
我们根据上面得到递推公式：
Pi+1=2−1×(X×(yi−1−yi)+Pi)P_{i+1}=2^{-1}\times(X\times(y_{i-1}-y_{i})+P_{i})Pi+1=2−1×(X×(yi−1−yi)+Pi)
P0=0P_{0}=0P0=0

yi-1	yi	操作
0	0	算术右移
0	1	减X后算术右移
1	0	加X后算术右移
1	1	算术右移

举例说明：
X=-3 Y=-2
[X]补=1101
[Y]补=1110
[X]变补=0011（减X时用）
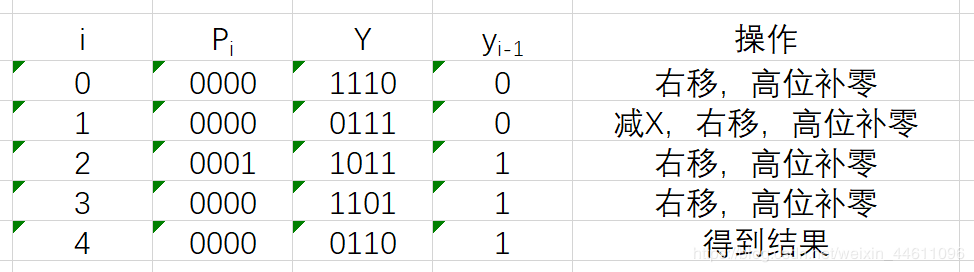
在这里插入图片描述
根据yi-1和yi两位来判断操作是什么，移位是算术移位，因为上面符号位始终都是0，所以每次都补0。
结果0000 0110表示+6，可以看出如果高四位全是0或1，则结果可以用4位数存放而不会溢出。
溢出判断：高四位不全为0或不全为1

补码两位乘运算

推导：
(1)Pi+1=2−1×(X×(yi−1−yi)+Pi)(1)P_{i+1}=2^{-1}\times(X\times(y_{i-1}-y_{i})+P_{i})(1)Pi+1=2−1×(X×(yi−1−yi)+Pi)
(2)Pi+2=2−1×(X×(yi−yi+1)+Pi+1)(2)P_{i+2}=2^{-1}\times(X\times(y_{i}-y_{i+1})+P_{i+1})(2)Pi+2=2−1×(X×(yi−yi+1)+Pi+1)
将(1)式代入(2)式得：
Pi+2=2−1×(X×(yi−yi+1)+2−1×(X×(yi−1−yi)+Pi))P_{i+2}=2^{-1}\times(X\times(y_{i}-y_{i+1})+2^{-1}\times(X\times(y_{i-1}-y_{i})+P_{i}))Pi+2=2−1×(X×(yi−yi+1)+2−1×(X×(yi−1−yi)+Pi))
Pi+2=2−1×2−1×(X×(2yi−2yi+1)+X×(yi−1−yi)+Pi)P_{i+2}=2^{-1}\times2^{-1}\times(X\times(2y_{i}-2y_{i+1})+X\times(y_{i-1}-y_{i})+P_{i})Pi+2=2−1×2−1×(X×(2yi−2yi+1)+X×(yi−1−yi)+Pi)
Pi+2=2−2×(X×(yi−1+yi−2yi+1)+Pi)P_{i+2}=2^{-2}\times(X\times(y_{i-1}+y_{i}-2y_{i+1})+P_{i})Pi+2=2−2×(X×(yi−1+yi−2yi+1)+Pi)

yi+1	yi	yi-1	操作	迭代公式
0	0	0	右移两位	2−2×(0+Pi)2^{-2}\times(0+P_{i})2−2×(0+Pi)
0	0	1	加X，右移两位	2−2×(X+Pi)2^{-2}\times(X+P_{i})2−2×(X+Pi)
0	1	0	加X，右移两位	2−2×(X+Pi)2^{-2}\times(X+P_{i})2−2×(X+Pi)
0	1	1	加2X，右移两位	2−2×(2X+Pi)2^{-2}\times(2X+P_{i})2−2×(2X+Pi)
1	0	0	减2X，右移两位	2−2×(−2X+Pi)2^{-2}\times(-2X+P_{i})2−2×(−2X+Pi)
1	0	1	减X，右移两位	2−2×(−X+Pi)2^{-2}\times(-X+P_{i})2−2×(−X+Pi)
1	1	0	减X，右移两位	2−2×(−X+Pi)2^{-2}\times(-X+P_{i})2−2×(−X+Pi)
1	1	1	右移两位	2−2×(0+Pi)2^{-2}\times(0+P_{i})2−2×(0+Pi)