B1计算机组成与体系结构——数据的表示

1.满十进一，满二十进二，以此类推……

2.按权（底数 * 指数）展开，第一位权值为10^0，第二位10^1……以此类推，第N位10^（N-1），该数的数值等于每位位的数值*该位对应的权值之和，

如 (1234)10 = 1* 10^3 + 2* 10^2 + 3*10 ^1 + 4*10^0;

由十进制到二进制，再到 N 进制，按权展开。

因为 b111 = o7 ,即一位八进制数字最大可由三位二进制数表示，  故 二进制转八进制时，先将二进制从右往左按3个数字划开，再写出对应的八进制数；

十六进制同理，按4位数划分。

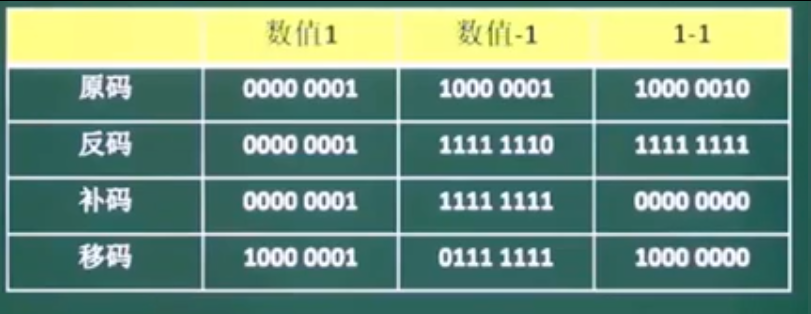
用8位数来表示码制，从左往右，第一位为符号位（高位，0表示正数，1表示负数）。

原码：正数，正常8位数二进制表示；负数，符号位为1，其余正常表示。

反码：正数，反码=原码；负数，在原码基础上，符号位不动，剩余位全部取反（0->1，1->0）。

补码：正数，补码=原码；负数，在反码基础上，符号位不动，加 1。

移码：正数，符号位取反（0->1）；负数，在补码基础上，符号位取反（1->0）。

补码常用作加减运算（超过8位，高位溢出）；移码做浮点数运算；

定点，定点整数就是位数全在点的左边，定点小数就是位数全在点的右边，点不占位数。

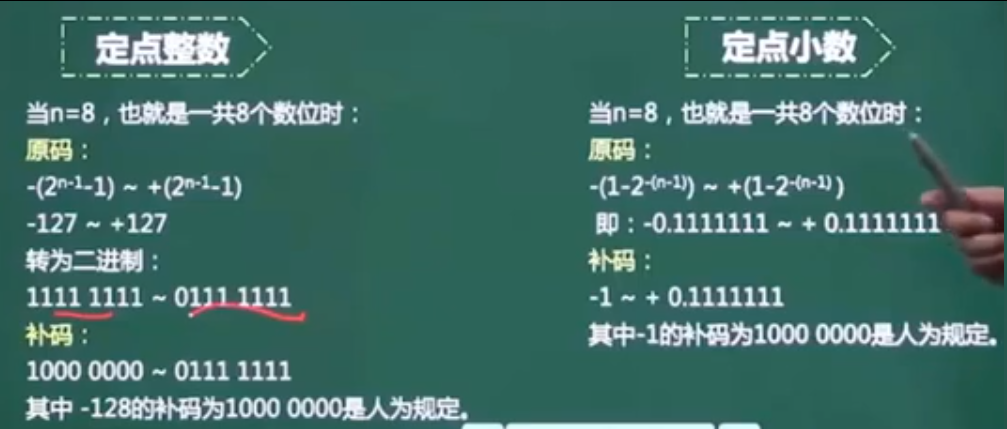
 浮点数

以 a = 3.14 x 10^3 为例：尾数：3.14，基数：10，指数：3;

同时，0.314 x 10^4，0.0314 x 10^5也可表示 a，阶码：3，4，5；

对阶，如 5.12 x 10^3 + 0.0314 x 10^5，0.0314 x 10^5应将尾数右移，变成 3.14 x 10^3，再来运算

尾数右移也可看做算术右移。

从熟悉的十进制出发，代入数字进行检验！

数据 计算机组成