06_第六章 广度优先搜索(bfs)
本章内容:
学习使用新的数据结构图来构建网络模型 学习广度优先搜索(breadth-first search BFS),你可对图使用这种算法诸如 “ 到x的最短距离是什么 ” 等问题 学习有向图和无向图 学习拓扑排序,这种排序算法指出了节点之间的依赖首先,这个图,不涉及x轴y轴,表示的节点以及各个节点之间的关系
广度优先搜索让你能够找出两样东西之间的距离,但是最短距离的含义有很多!使用广度优先搜索可以:
编写国际跳棋AI,计算走多少步就可以获胜; 编写拼写检查器,计算最少编辑多少个地方就可以将错的单词改为正确的; 根据你的人际关系找人。图算法应该是最有用的!
目录
1 图简介
1.1 问题一(最短路径是是什么)
1.2 图是什么
2 广度优先搜索
2.1 问题二(有无最短路径)
2.2 队列
3 实现图和算法
3.1 解决问题二
3.2 解决问题一
4 运行时间
5 小结
1 图简介 1.1 问题一(最短路径是是什么)比如,猪猪家在浙江,猪猪很想念珊珊,猪猪想要去珊珊家,珊珊家在湖南,希望走的省份越少越好,希望早点见到珊珊!
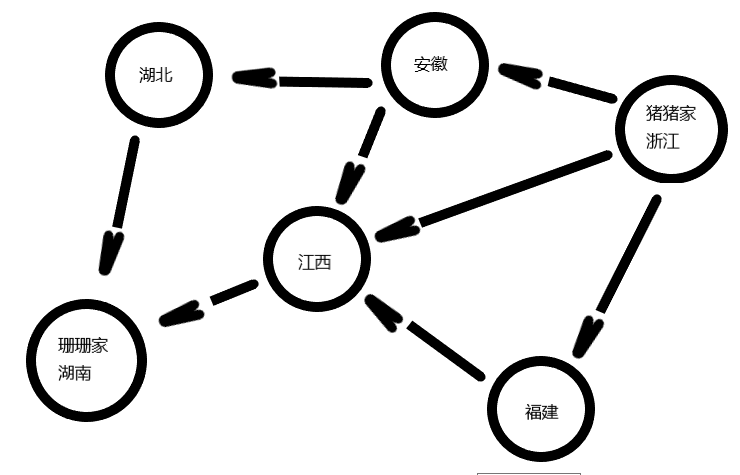
那么,最快的方案是什么?
浙江——江西——湖南,两步到达珊珊家
要确定如何从浙江前往湖南,需要两个步骤:
使用图来建立问题模型 使用广度优先搜索解决问题这个问题留在后面解决!
1.2 图是什么很简单,图是由节点(node)和边(edge)组成

一个节点可能和众多节点直接相连,这些节点被称为邻居。如果不直接相连那么便不是邻居。
图用于模拟不同的东西是如何相连的。
2 广度优先搜索广度优先搜索可以回答两类问题:
第一类问题:从节点A出发,有前往节点B的路径吗? 第二类问题:从节点A出发,前往节点B的哪一条路最短? 2.1 问题二(有无最短路径)朋友是你的一度关系,朋友的朋友便是你的二度关系,在你看来,一度关系甚于你的二度关系。
也就是说,先从一度关系里面去找,要是找不到,那么从二度关系里面找。

必须按照添加的顺序开始检查,有一个可以实现这种目的的数据结构就是——队列(queue)
2.2 队列用七个字概括一下队列:先进先出的数组(first in first out FIFO)
提示:更新队列的时候,可使用术语“入队”和“出队”,或者是术语“压入”和“弹出”,都一个意思
在Python中,可使用函数deque来创建一个双端队列,deque模块是python标准库collections中的一项。
我这里参照网上的教程总结了大部分的应用:
import collections
#或者是:from collections import deque
d = collections.deque()
#或者是:d = deque()
#创建双向队列
d.append(1)
d.append(2)
print(d)
#deque([1, 2])
#从右边添加一个元素
d.appendleft(3)
print(d)
#deque([3, 1, 2])
#从左边添加队列
d.clear()
#清空队列
d.copy()
#拷贝队列
d.count(2)
#返回指定元素2的出现次数
d.extend([1,6,4])
d.extendleft([1,6,4])
#从队列 右边/左边 扩展一个列表的元素
d.index(6)
#查找某个元素的索引位置
d.insert(2,"b")
#在指定位置插入元素
d.pop()
d.popleft()
#获取 右边/左边 的一个元素,并在队列中删除
d.remove("b")
#指定删除的元素
d.reverse()
#队列反转
d.rotate(2)
#把右边的元素放到左边,默认为1,这里指定操作两次
3 实现图和算法
首先,需要用代码来实现图。图由多个节点组成。
每个节点都与临近的节点相连,如果表示类似于 ” 你 ——> Bob “ 这样的关系呢?散列表这个结构可以好好的表示这样的关系。
在这里,散列表将节点映射到其所有的邻居。
3.1 解决问题二
对于 ” you “ 这个节点和邻居的映射关系的python代码如下:
graph = {}
graph["you"] = ["alice","bob","claire"]
注意 ” you ” 被映射到了一个数组,因此graph["you"]是一个数组,其中包含了“you”的所有的邻居
Anuj、Peggy、Thom、Jonny都没有邻居,这里因为虽然有指向他们的箭头,但是没有从他们出发指向其他人的箭头。这被称为有向图(directed graph),其中的关系是单项的。因此,Anuj是Bob的邻居,但是Bob不是Anuj的邻居。无向图(undirected graph)没有箭头,直接相连的节点互为邻居,相当于互相所指的有向图。
因此,对于图的所有的映射关系的python代码如下:
graph = {}
graph["you"] = ["alice","bob","claire"]
graph["bob"] = ["anuj",'geggy']
graph['alice'] = ['peggy']
graph['claire'] = ['thom','jonny']
graph['anuj'] = []
graph['peggy'] = []
graph['thom'] = []
graph['jonny'] = []
print(graph)
#输出
{'you': ['alice', 'bob', 'claire'], 'bob': ['anuj', 'geggy'], 'alice': ['peggy'], 'claire': ['thom', 'jonny'], 'anuj': [], 'peggy': [], 'thom': [], 'jonny': []}
另外,由于散列表是无序的,因此无需管散列表中的键值对的顺序。
首先,使用函数deque来创建一个双端队列
from collections import deque
serach_queue = deque()
serach_queue.extend(graph['you'])
print(serach_queue)
#输出
deque(['alice', 'bob', 'claire'])
再来看看其他代码,循环语句来判断有无芒果销售商
while serach_queue:
#只要队列不为空,循环就一直继续
person = serach_queue.popleft()
#从队列的左侧取出第一个人
if person_is_mango_seller(person):
#这个函数判断这个人是不是芒果销售商,如果是返回Ture,执行if语句
print(person + 'is a mango seller!')
else:
#如果这个人不是芒果销售商,那么执行else语句
serach_queue.extend(graph[person])
#把这个人的邻居都加入到搜索队列当中
对于判断这个人是芒果销售商的函数如下:
(只要名字的最后一个字母是m,那么就是对的人)
def person_is_mango_seller(name):
return name[-1] == 'm'
但是有个问题,发现没有。peggy既是alice的好友又是bob的好友,因此ta两次加入到队列中。因此搜索队列中会有两个peggy,不仅做了无用功,而且若是有无向图的情况会导致无向图之间的无限循环。因此,在检查一个人之前,需要判断这个人有没有检查过。
考虑这一点后,广度优先搜索的最终代码如下:
from collections import deque
graph = {}
graph["you"] = ["alice","bob","claire"]
graph["bob"] = ["anuj",'peggy']
graph['alice'] = ['peggy']
graph['claire'] = ['thom','jonny']
graph['anuj'] = []
graph['peggy'] = []
graph['thom'] = []
graph['jonny'] = []
def person_is_mango_seller(name):
return name[-1] == 'm'
def serach(name):
serach_queue = deque()
serach_queue.extend(graph[name])
serached = []
#用于记录已经被查找过的人
while serach_queue:
#只要队列不为空,循环就一直继续
person = serach_queue.popleft()
#从队列的左侧取出第一个人
if person not in serached:
if person_is_mango_seller(person):
#这个函数判断这个人是不是芒果销售商,如果是返回Ture,执行if语句
return (person + ' is a mango seller!')
else:
#如果这个人不是芒果销售商,那么执行else语句
serach_queue.extend(graph[person])
#把这个人的邻居都加入到搜索队列当中
searched.append(person)
return ("without mango seller!")
print(serach('you'))
#输出
thom is a mango seller!
OK, the second programe have solved !
3.2 解决问题一
显然,解决完我们的问题二,我们可以得到时候存在最短路径。但是对于问题一而言,我们已经知道一定存在最短路径,求解的目标是找出那条最短路径。于是,我们需要在前一个问题的基础之上,加以改进,代码如下:
from collections import deque
place = {}
place["zhejiang"] = ["anhui","jiangxi","fujian"]
place["anhui"] = ["hubei",'jiangxi']
place['jiangxi'] = ['hunan']
place['fujian'] = ['jiangxi']
place['hubei'] = ['hunan']
place['hunan'] = []
start = 'zhejiang'
end = 'hunan'
#这个函数返回的是遍历每一个顶点的顺序
def serach(site_name):
serach_queue = deque()
serach_queue.extend(place[site_name])
serached = []
while serach_queue:
site = serach_queue.popleft()
if site not in serached:
if site == end:
break
else:
serach_queue.extend(place[site])
serached.append(site)
allline_for_serached = ['zhejiang'] + serached + ['hunan']
return allline_for_serached
#这个函数打印出在可求的最短路径中找出那条最短路径
def find_shortest_line(allline_for_serached):
#‘hunan’作为最后一个节点
every_end = 'hunan'
shortest_line = [every_end]
#只要没有遍历到起点‘浙江’,那么继续
while every_end != start:
#遍历allline_for_serached的顶点
for i in allline_for_serached:
#如果找得到节点every_end的父节点
if every_end in place[i]:
#将父节点加入到队列当中去
shortest_line.append(i)
#替换父节点,将其变成子节点,继续找父亲的父亲
every_end = i
#break跳出当前的for循环回到执行while语句
break
return shortest_line[::-1]
print(serach(start))
print(find_shortest_line(serach(start)))
#输出
['zhejiang', 'anhui', 'jiangxi', 'fujian', 'hubei', 'hunan']
['zhejiang', 'jiangxi', 'hunan']
对于这个问题你有没有这样想过,对于路径图而言,这里指向”湖南“的节点有好多个,但是在上述代码当中,只要找到了一个父节点就不会再去找第二个父节点了,这个是为什么呢?
因为广度优先搜索所找的路径就是最短路径,最短路径要么只有一条,要么就是几条相同长度的路径。因此,代码中即便一个节点有多个父节点,但是找出来的那一条路一定是最短路径。然而这也有一个问题,就是,要是最短路径有多条,那么这个方法只能找出其中的一条。
OK, the first programe have solved !
现在有这样一个问题,是原来第一个问题的加强版,要求计算猪猪到珊珊家的最短路程。
地图路线里程如下:
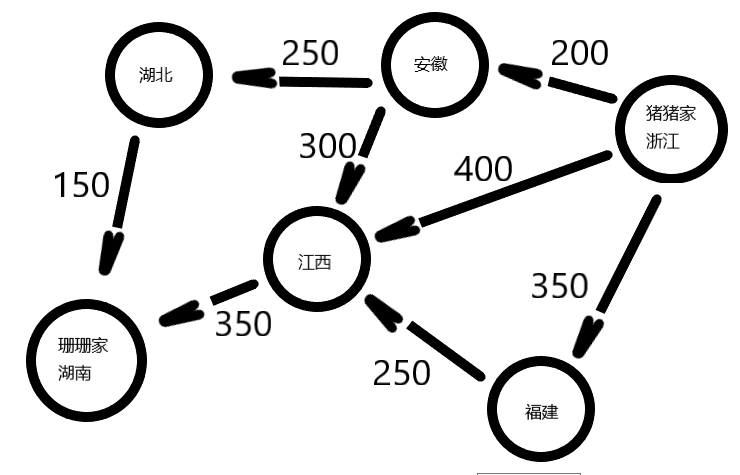
相对于上一个问题,大部分的东西都没有变,多的只是节点之间的边有了相对应的数据。
这个问题怎么解决呢?答案在下一章!因为广度优先搜索无法解决这一类加权图的问题!
4 运行时间
由于广度优先搜索是对每一个节点进行搜索,就意味着你将沿每一条边前行(记住,边是从一个人到另一个人的箭头或连接),因此运行时间至少为 O(边数)
你还使用了队列,其中包含检查的每一个人。将一个人添加到队列里面需要的时间是固定的,即O(1),因此对于每一个人做这样的事情就需要时间O(人数)。
所以广度优先搜索的运行时间为 O(人数+边数) ,这个通常写作 O(V+E) ,其中V为顶点数(vertice),E为边数。
另外,从某种程度上来说,列表是有序的。如果任务A依赖于任务B,在列表中任务A就必须在任务B的后面。这个被称作拓扑排序。
此图即为此树!哈哈哈
5 小结
这一章的内容比较多,还是小结一下:
广度优先搜索可以解决有无从A到B的路径以及最短路径是什么
广度优先搜索只适用无权重的图,占用内存比较多,但是速度比较快
对于检查过的人一定不要再去检查,否则可能导致无限循环
 手可摘星辰不敢高声语
手可摘星辰不敢高声语
 原创文章 8获赞 2访问量 369
关注
私信
展开阅读全文
原创文章 8获赞 2访问量 369
关注
私信
展开阅读全文
作者:手可摘星辰不敢高声语