Leetcode 刷题(12)队列应用:广度优先搜索求完全平方数
题目
63. 完全平方数
作者:吕诺

难度:中等
题目分析:找一个和的可能拆分,在不清楚数学解析解的时候,就是一个状态空间搜索的问题。对于搜索问题,有两种策略。一种是广度优先搜索,即BFS;另一种是深度优先搜索,即DFS。这里答案是需要我们找到个数最少的拆分,所以,用广度优先搜索是最合适的策略。使用深度优先搜索,只能是找到所有解后,从中确定最优解。
这道题不要求我们写出拆分方式,只要个数,所以,最合适的是BFS。
from collections import deque
class Solution:
def numSquares(self, n: int) -> int:
# 平方数最少,那肯定从最大的开始试
# 可以递归,可以自己调用队列
# 定义一个辅助函数,先算出最大的平方数可以是多少
# 结束条件有两个,一是等于(这就是解),二是大于(要排除)
if n == 1:
return 1
k = self.maxInt(n) # 算出最大的k,之后从k遍历递减到1
if k*k == n:
return 1
ans_list = [n] # 储存for循环里面的步数
for num in range(k, 1, -1): # 多个起点
temp_q = deque()
res = n
step = 0
temp_q.append((res, num, step)) # num是下一个测试的元素,step是当前步数
while len(temp_q):
res, test_n, step = temp_q.popleft()
res = res - test_n * test_n
step += 1
# 这个if增加了,解答就错了!
# if res < 4:
# ans_list.append(step + res)
# break
# res 有没有可能小于 0?
for ii in range(test_n, 1, -1):
if ii * ii == res:
ans_list.append(step + 1)
temp_q = deque() # 清空队列,为了退出while循环
break
elif ii * ii < res:
temp_q.append((res, ii, step))
else: # ii平方大于 res, 不需要储存
pass
return min(ans_list)
def maxInt(self, n):
'''
求当前数字n,能接收的最大平方数是多少
'''
# 更快的解法,求平方根啊!虽然平方根里面也有循环
i = 1
while i*i <= n:
i += 1
return i - 1
分析:
探索各种情况的时候,没有记录,导致重复探索,最后程序运行超时
简单求平方根,使用了笨拙的while循环,其实用开根或是指数求解即可
增加了冗余的条件,使答案出错:
# 这个if增加了,解答就错了!
# if res < 4:
# ans_list.append(step + res)
# break
解法一:标准BFS
from collections import deque
class Solution:
def numSquares(self, n: int) -> int:
# 参考评论区标准的BFS解法,很有启发性
my_queue = deque() # 存储探索的位置
visited = set() # 存取已经求过的和,先存入的,肯定是距离最短
# 这里不采用减法,而是使用加法,可以省去余数,求平方根的过程
step = 0
my_queue.append(0) # 出发点
visited.add(0) # 已经探索的值
while len(my_queue): # 要遍历到队列结束
size = len(my_queue)
step +=1 # 此时队列size个数,是同一层能达到的距离
for i in range(size):
cur = my_queue.popleft() # 取出
j = 1
while j * j + cur <= n:
next = j * j + cur
if next == n: # 找到了
return step
if next not in visited:
visited.add(next)
# 加入队列是关键
my_queue.append(next)
j += 1
return step
运行结果:
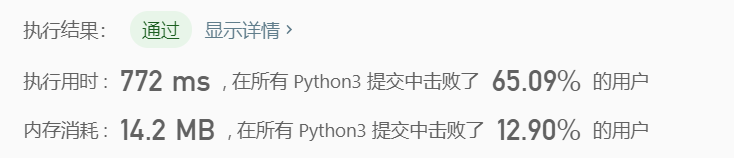


这个方法也不能说慢
在队列元素出队之前,求size, 使用for循环,是为了把统一距离的中间节点,再同时往前推;这样做的好处,就是能明确区分每一步。如果不使用size这个for循环,那么队列不仅要存储当前的数,还要存储步数。
解法二: 基于减法策略的BFS使用减法,结合了上述分步数的优势
from collections import deque
class Solution:
def numSquares(self, n: int) -> int:
# 尝试使用减法来求解
my_queue = deque()
visited = set()
step = 0
# 起始点入队
my_queue.append(n)
visited.add(n) # 其实可以不加
while len(my_queue): # 队列有元素
size = len(my_queue) # 可以区分步数而减少存储,两种都试
step += 1
for i in range(size):
cur = my_queue.popleft()
res = [cur - j*j for j in range(1, int(cur**0.5) + 1)]
for r in res:
if r == 0: # 找到解
return step
# 这里都是 r > 0的
if r not in visited: # 第一次出现
visited.add(r)
my_queue.append(r) #
# 这里可以不用返回
运行结果:

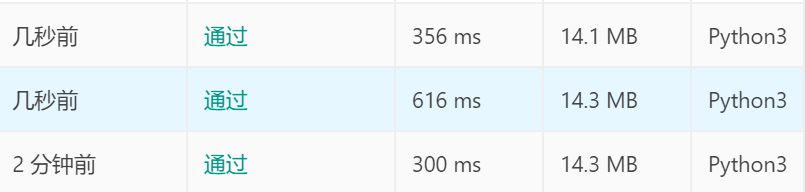
运行了3次,这个方法大概率是更快的,因为引入了for循环代替while循环
from collections import deque
class node:
def __init__(self,value,step=0):
self.value = value
self.step = step
def __str__(self):
return ''.format(self.value,self.step)
class Solution:
def numSquares(self, n: int) -> int:
queue = [node(n)]
visited = set([node(n).value])
while queue:
vertex = queue.pop(0)
residuals = [vertex.value - n*n for n in range(1,int(vertex.value**.5)+1)]
for i in residuals:
new_vertex = node(i, vertex.step+1)
if i==0:
return new_vertex.step
elif i not in visited:
queue.append(new_vertex)
visited.add(i)
return -1
运行结果:

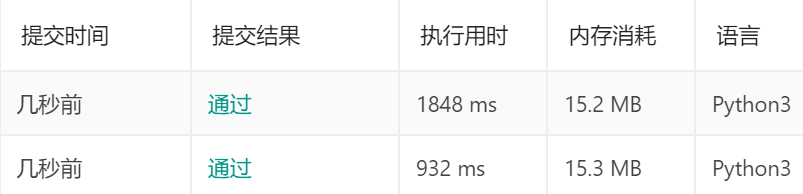

是真的慢!
因此,对于追求性能的应用来说,单独定义类还是要避免。虽然定义成类,对于数据的封装和安全性,非常有帮助。
解法三:动态规划,比较巧妙的方法但是却很慢
class Solution:
def numSquares(self, n: int) -> int:
dp = [0]*(n+1) # 建立一个比n多一个的数组,存储其需要的因子数
for i in range(1, len(dp)):
dp[i] = i # 理论上,总可以用1来拼出需要的数
j = 1
while i - j *j >= 0:
dp[i] = min(dp[i], dp[i - j*j] + 1) # dp[i]负责存储当前最小的数
j += 1 # 其实是在遍历
return dp[n]
运行结果:

!!!慢到出不了结果……这里面重复遍历的地方太多了!
类似递归的解法。
作者:吕诺