二叉查找树,AVL树
二叉查找树
若它的左子树不为空,则左子树上所有的节点值
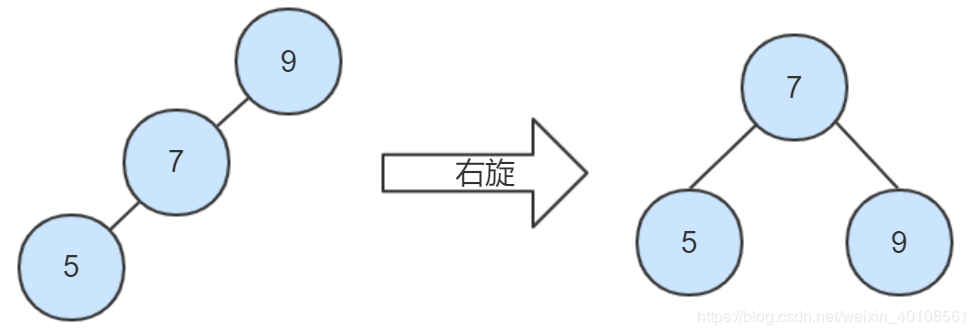 右-右型:左旋。
右-右型:左旋。
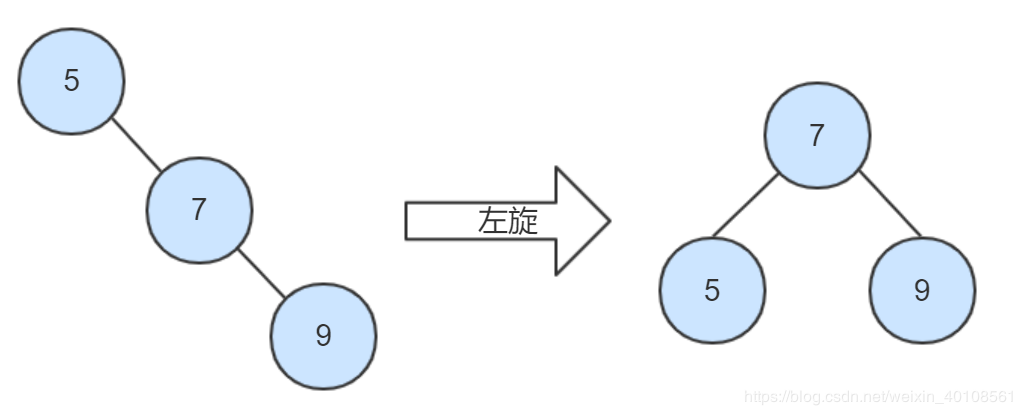 左-右型:先
左-右型:先
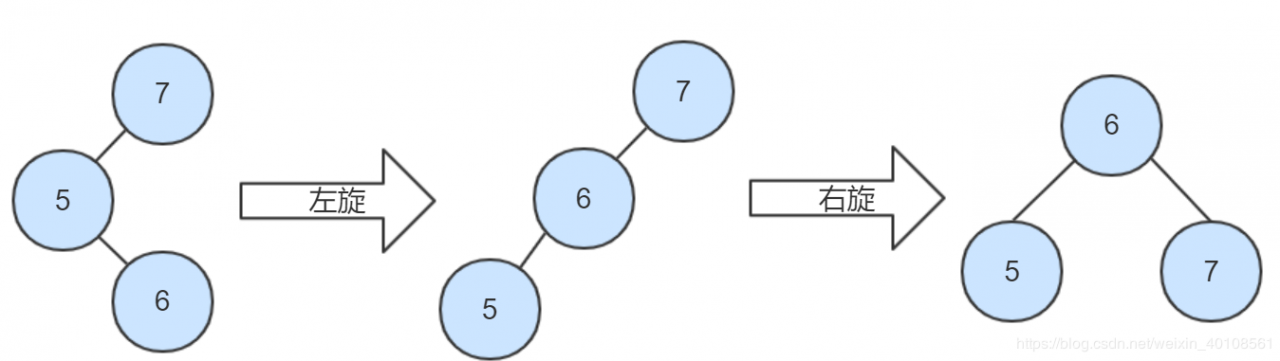 右-左型:先
右-左型:先
作者:KeyboardMan6
都小于它的根节点值。
若它的右子树不为空,则右子树上所有的节点值都大于它的根节点值。
它的左右子树也分别可以充当为二叉查找树。
查找的平均复杂度是O(log(n))的,最坏情况是O(N)的。
查找所需的次数是二叉查找树的最大深度。
AVL树(平衡二叉查找树)
具有二叉查找树的全部特性。
每个节点的左子树的高度和右子树高度差值小于等于1(平衡二叉树的性质)
左旋:逆时针旋转两个节点,原先的右节点成为新的父节点,原先的父节点成为原先的右节点的左节点。如果原先的右节点有左节点,则将该左节点挂到原先的父节点的右侧。
右旋:顺时针旋转两个节点,原先的左节点成为新的父节点,原先的父节点成为原先的左节点的右节点。如果原先的左节点有右节点,则将该右节点挂到原先的父节点的左侧。
调整规则如下:
左-左型:右旋。 右-右型:左旋。
右-右型:左旋。 左-右型:先
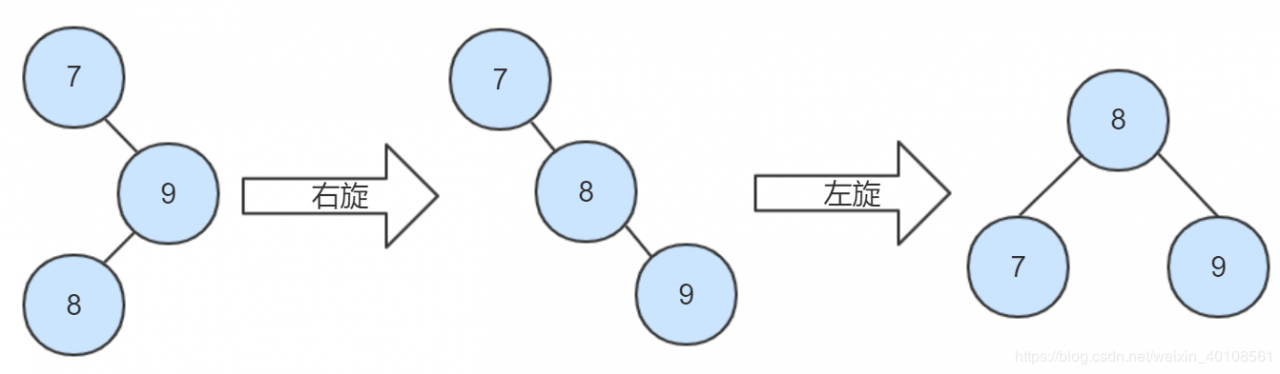
左-右型:先左旋左节点和该左节点的右节点(交换),再右旋父亲节点和左节点。 右-左型:先
右-左型:先右旋右节点和该右节点的左节点(交换),再左旋父亲节点和右节点。
作者:KeyboardMan6