Java实现二叉查找树的增删查详解
目录
定义
增加节点
查询节点
删除节点
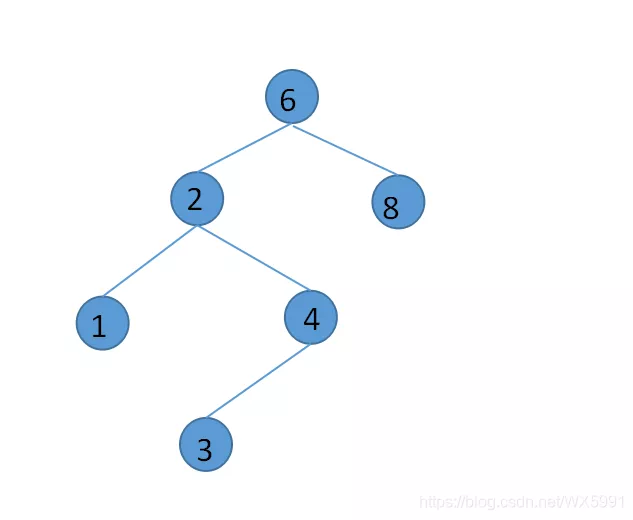
定义二叉查找树(ADT)是一个具有对于树种的某个节点X,它的左节点都比X小,它的右节点都比X大的二叉树。如下就是一个符合
要求的二叉查找树:
1.定义节点类:
class Node{
int val;
Node left;
Node right;
public Node(int val){
this.val=val;
}
}
2.插入元素
我们采用递归的方法:
1.判断与根节点是否相同,相同无需操作
2.比根元素小往左边查找,左节点不存在的话则作为左节点插入即可
3.比根元素大往右边查找,右节点不存在的话则作为右节点插入即可
代码实现如下:
Node root;
/**
* 添加元素
* @param val
*/
public void add(int val){
if(root==null){
root=new Node(val);
return;
}
addNode(val,root);
}
private void addNode(int val,Node root){
if(root==null || root.val==val){
return;
}
if(root.val>val){
if(root.left==null){
root.left=new Node(val);
}else {
addNode(val,root.left);
}
}else {
if(root.right==null){
root.right=new Node(val);
}else {
addNode(val,root.right);
}
}
}
查询节点
我们采用递归的方法:
1.判断与根节点是否相同,相同则返回true
2.比根元素小往左边查找,左节点为null则返回false表示不存在
3.比根元素大往右边查找,右节点为null则返回false表示不存在
代码实现如下:
/**
* 判断指定值是否存在
* @param val 指定值
* @return true--存在 false--不存在
*/
public boolean findVale(int val){
return isExit(root,val);
}
private boolean isExit(Node node,int val){
if(node==null){
return false;
}
if(node.val==val){
return true;
}else if(node.val>val){
return isExit(node.left,val);
}else {
return isExit(node.right,val);
}
}
删除节点
删除元素时要判断元素的情况:
1.删除的元素没有叶子节点,直接删除,如删除值为1的节点,虽然平衡性不是太好,但是还是符合二叉查找树的特性
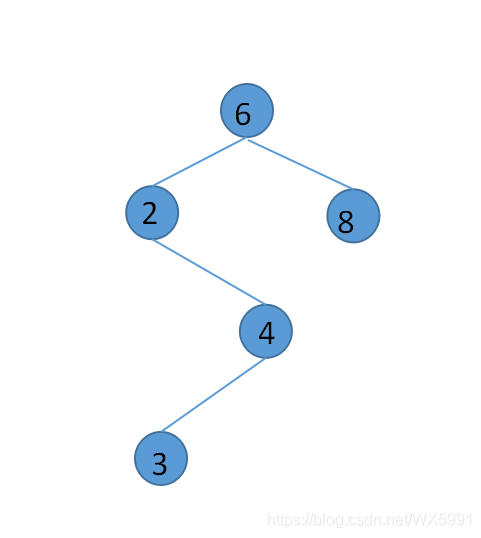
2.删除的元素只有一个节点,删除元素并将指针指向其子节点 ,如删除值为4的节点:
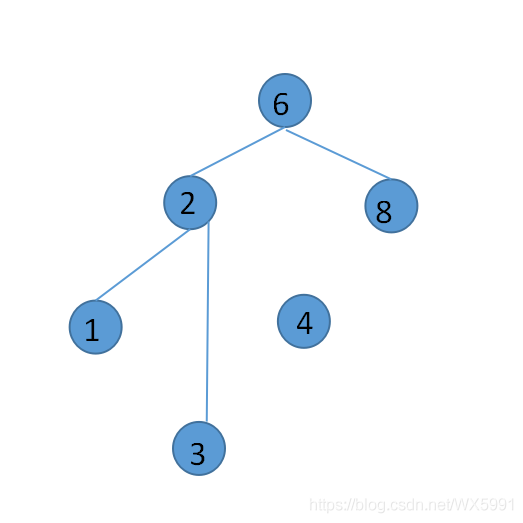
3.删除的元素有左右两个节点,从右节点中找出大于该节点的最小节点,作为新的节点A,如删除节点值为2的节点:

代码实现如下:
/**
* 删除元素
* 1.删除的元素没有叶子节点,直接删除
* 2.删除的元素只有一个节点,删除元素并将指针指向其子节点
* 3.删除的元素有两个节点,从右节点中找出大于该元素的最小值,作为新的节点
* @param val
*/
public void deleteElement(int val){
deleteElement(null,root,val,true);
}
/**
* 删除元素
* @param prev 父节点
* @param root 当前节点
* @param val 删除值
* @param isright 是否是右节点
*/
private void deleteElement(Node prev,Node root,int val,boolean isright){
if(root.val==val){
//删除的元素没有叶子节点,直接删除
if(root.left==null && root.right==null){
changeValue(prev,null,isright);
}else if(root.left!=null && root.right!=null){
//3.删除的元素有两个节点,从右节点中找出大于该元素的最小值,作为新的节点
changeValue(prev,new Node(findMinGt(root,root.right,true)),isright);
if(prev==null){
//对于头结点的删除特殊处理
prev=this.root;
prev.left=root.left;
prev.right=root.right;
return;
}
if(isright){
prev.right.right=root.right;
prev.right.left=root.left;
}else {
prev.left.right=root.right;
prev.left.left=root.left;
}
}//删除的元素只有一个节点,删除元素并将指针指向其子节点
else if(root.left!=null){
changeValue(prev,root.left,isright);
}else {
changeValue(prev,root.right,isright);
}
return;
}
if(root.val>val){
deleteElement(root,root.left,val,false);
}else{
deleteElement(root,root.right,val,true);
}
}
//改变元素值
private void changeValue(Node prev,Node value,boolean isright){
if(prev==null){
root=value;
return;
}
if(isright){
prev.right=value;
}else {
prev.left=value;
}
}
//寻找大于根节点的最小值
private int findMinGt(Node prev,Node root,boolean isRight){
if(root.left==null && root.right==null){
changeValue(prev,null,isRight);
return root.val;
}
if(root.left==null){
changeValue(prev,null,isRight);
return root.val;
}
return findMinGt(root,root.left,false);
}
到此这篇关于Java实现二叉查找树的增删查详解的文章就介绍到这了,更多相关Java二叉查找树增删查内容请搜索软件开发网以前的文章或继续浏览下面的相关文章希望大家以后多多支持软件开发网!