潜析AVL树--AVL树的双旋转
接上篇博文:简析AVL树–AVL树的概念及单旋转
AVL树如何恢复平衡之双旋转首先假设我们有一颗已经处于平衡的AVL树:
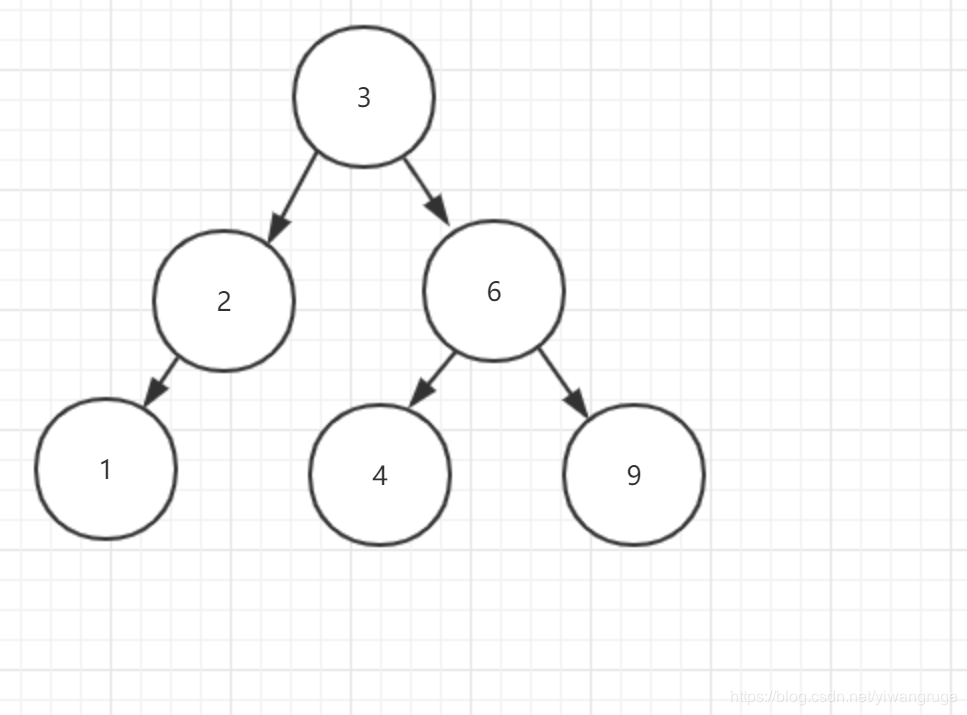
上篇博文已经解决了LL和RR两种情况的平衡恢复解决方案----单旋转。这篇博文来看双旋转情形。这时候我们插入结点7,我们可以发现这时这棵树并没有失去平衡:
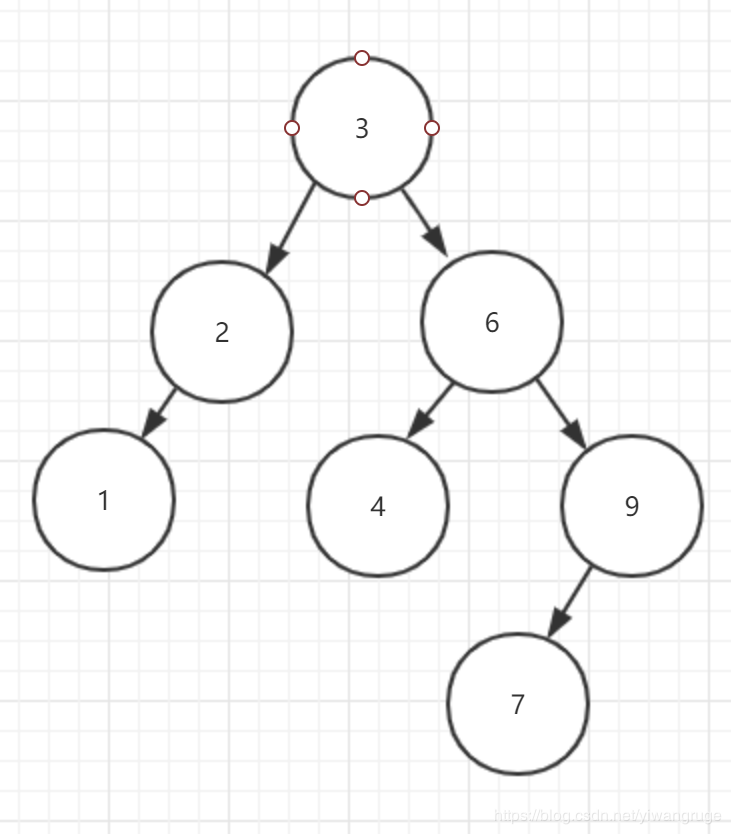
但是,如果我们继续插入结点8,这棵树就会再次处于失衡状态:
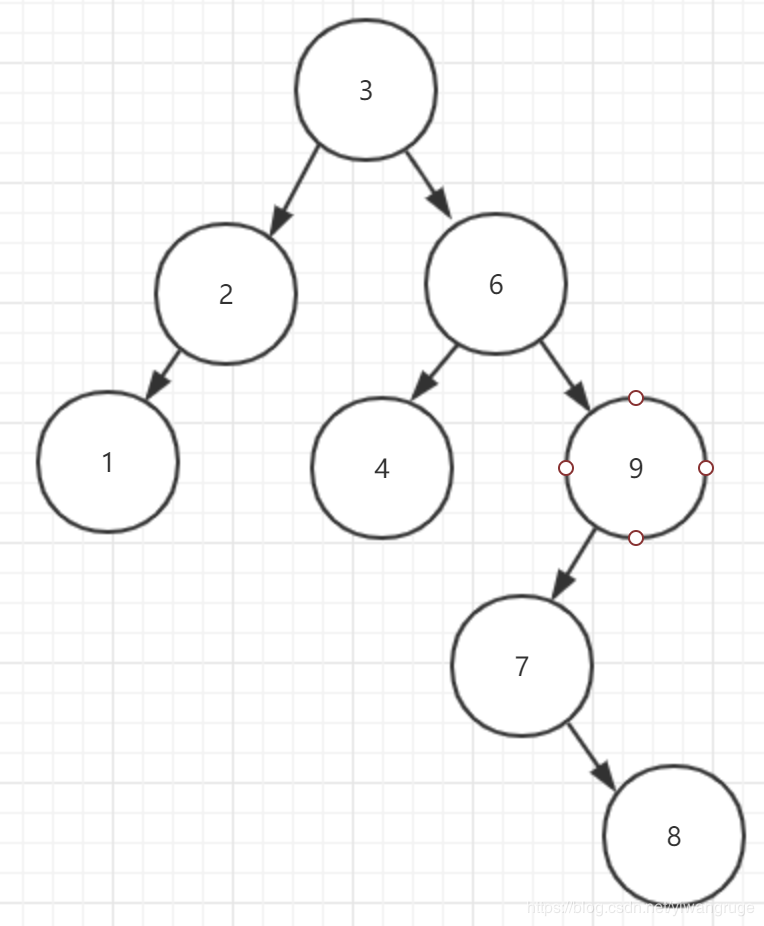
我们首先可以发现结点9左右子树高度差2—这是第一个失衡的结点。
然后我们可以发现结点6左右子树高度差2—这是第二个失衡的结点。
最后发现根节点3也失衡了—它的左右子树高度同样差2。
我们首先从离插入的结点8最近的结点9开始处理。为了方便起见我们将结点9单独提出来考虑:
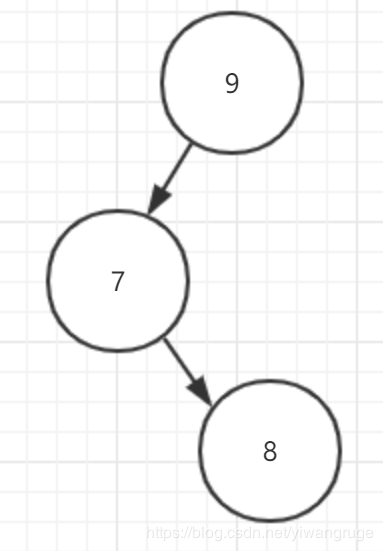
可以看到此时结点9失衡的原因是结点9的左儿子(L)的右子树(R)被插入了新结点8。如果我们这时候尝试单旋转对它进行修复,我们会发现这种修复方式无效:
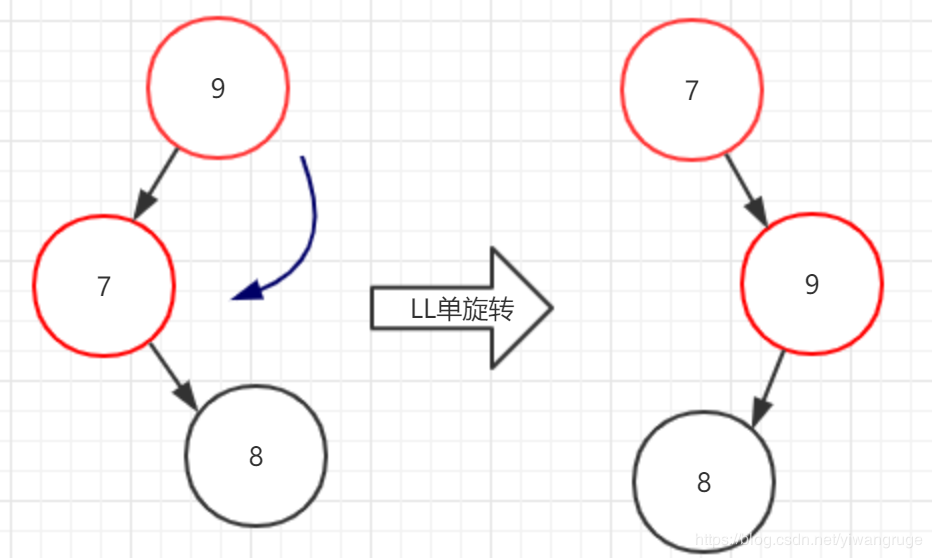
但是,我们这样想:如果先将结点7和结点8执行RR单旋转,那么这棵树就变成了LL单旋转可修复情形了:
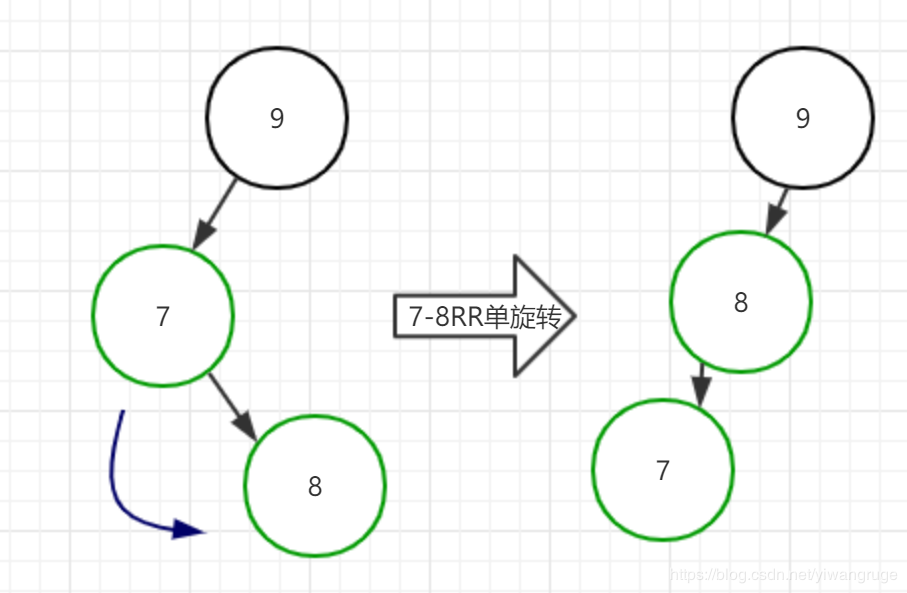
然后我们可以执行LL单旋转进行修复:
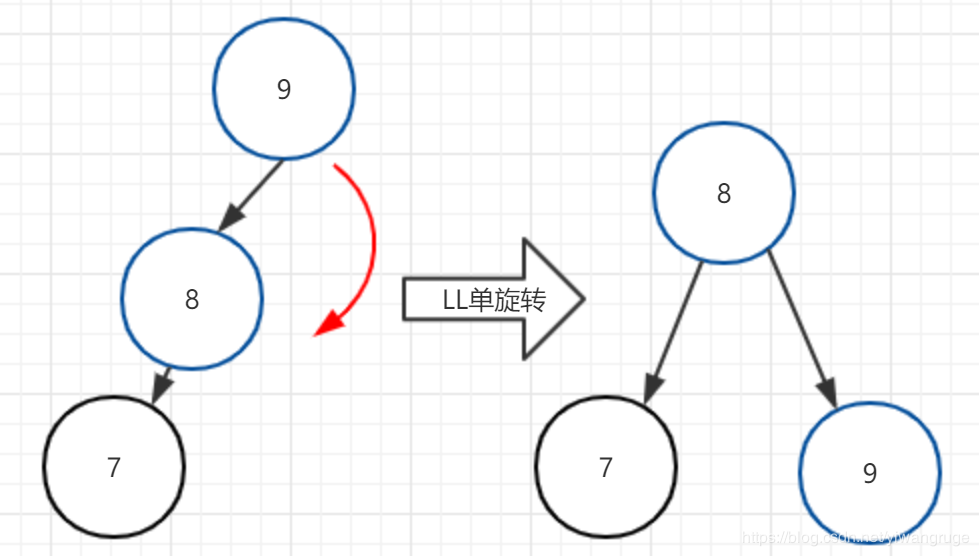
如上图所示,我们成功地将新插入结点8而造成的失衡成功通过两次单旋转修复,这种修复的方式我们称为LR双旋转(因为树的失衡原因是在结点9的左儿子的右子树插入了新结点)。有些童鞋可能会担心旋转之前结点8可能还会有左右儿子从而被覆盖丢失,其实无需担心,因为执行的两次单旋转里已经考虑到了这个问题而对结点8的左右儿子进行了挪动。
通过上面这个例子,我们可以总结LR双旋转的伪代码如下:
对当前结点的左儿子进行RR单旋转;
对当前结点进行LL单旋转;
返回旋转后结果;
执行完一次修复后此时整棵树如下:
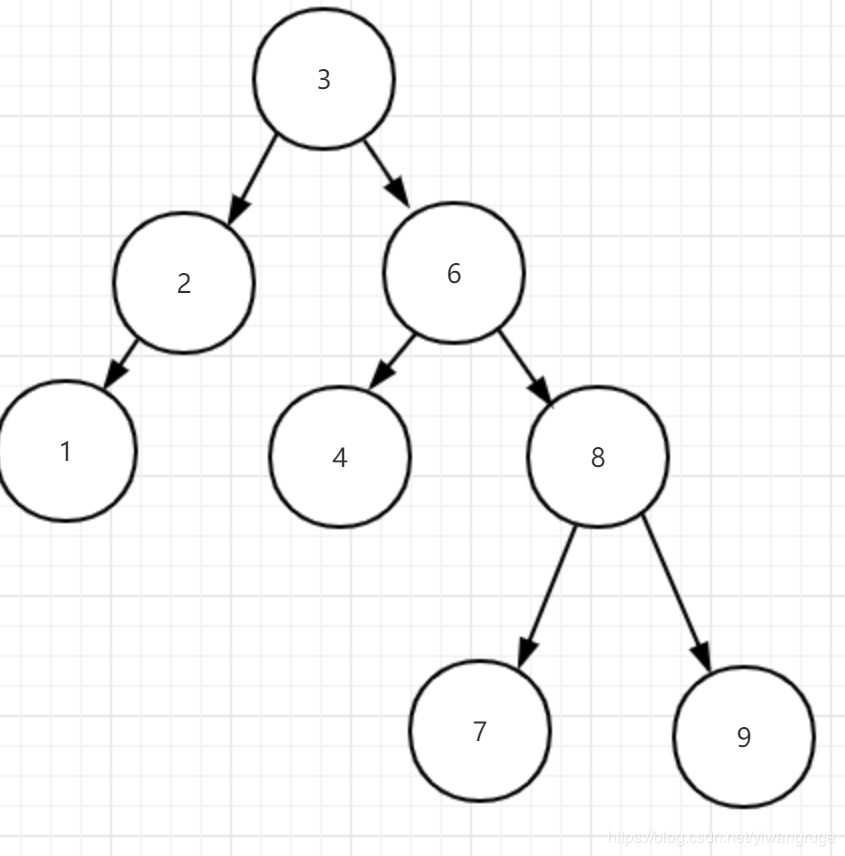
我们发现这棵树再次平衡了–结点6和结点3也平衡了,这是因为本身这两个结点失衡的原因就是结点6、结点3的右子树高度改变了,修复之后,自然就平衡了。
对应的,假如上面失衡的情况是这样的:
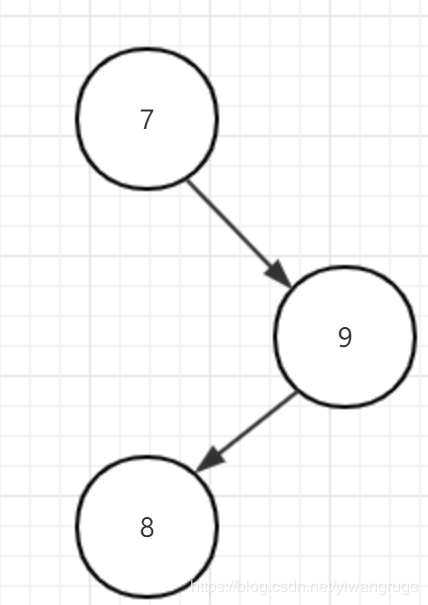
这种情况称为RL失衡。我们可以通过进行RL双旋转来进行修复,即先对结点9和结点8进行一次LL单旋转,再对整棵树进行一次RR单旋转:
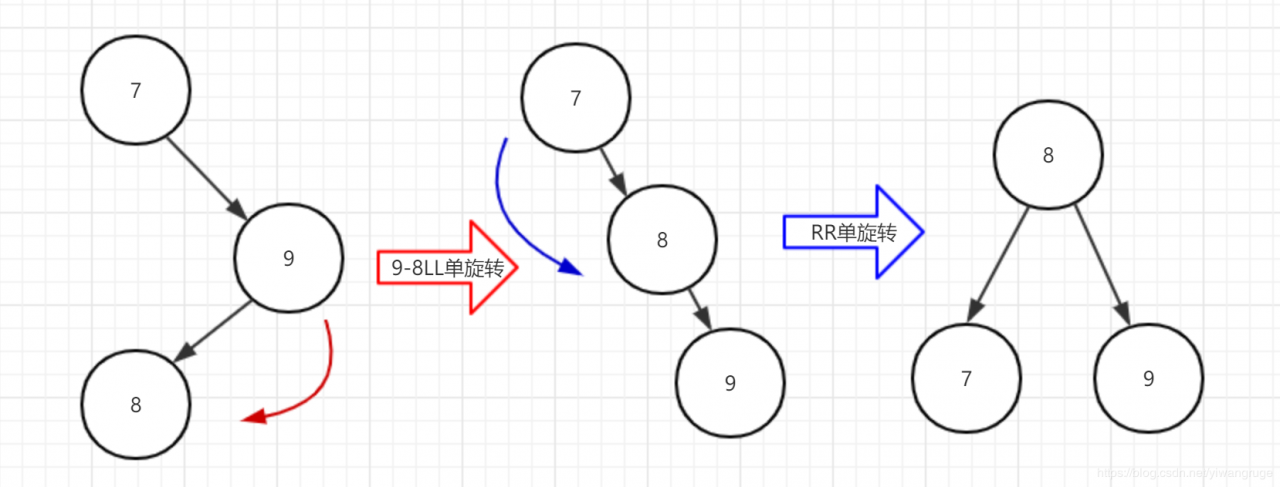
我们可以总结出RL双旋转的伪代码如下:
对当前结点的右儿子进行LL单旋转;
对当前结点进行RR单旋转;
返回旋转后结果;
关于AVL树的C++实现请看下篇博文:
潜析AVL树–AVL树的C++实现
作者:一只巴扎黑