知识蒸馏论文读书笔记

突然觉得，我应该做一点笔记，梳理一下学过的东西，否则年一过，整个人就跟失忆了一样。
知识蒸馏这个名字非常高大上（不得不说大佬不仅想法清新脱俗，名字也起的情形脱俗啊）。如果直白地说老师学生模型，那就不酷了。
下面是论文的总结梳理，

第一次尝试-Model Compression

在2015年hinton 的知识蒸馏文章发表出来之前，就有人尝试过让一个小模型去学习一个大模型的表现，以期能够达到与大模型等同的性能。
这篇文章的标题就叫“Model Comperssion”，是2006年的文章，大家都还在用CPU训练模型，不会有什么很大的神经网络是需要大家去压缩。这里的需要被压缩的“Model”是一个集成学习的模型。
作者在文中提到的压缩集成学习模型的目的与现在压缩神经网络的原因如出一辙。

集成模型往往体积大且运算缓慢，这使得集成学习算法在面对低内存，低空间（应该是硬盘），低运算能力，以及实时性要求高的场景下比较无力。

模型压缩的流程也比较类似。

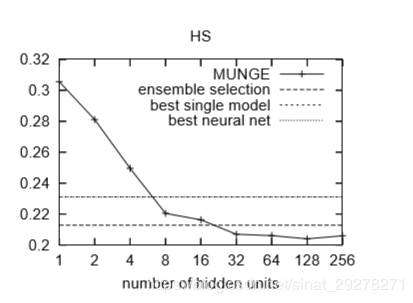
用训练数据训练D1D_1D1​集成学习模型TTT 用MUNGE算法生成无标签数据，将无标签数据作为TTT的输入，得到相应的标签得到人工数据集D2D_2D2​ 用人工数据集D2D_2D2​训练神经网络模型S1S_1S1​ 用原始数据D1D_1D1​训练神经网络模型S2S_2S2​作为对照组

上面提到的MUNGE算法，是一个数据生成算法，目的是生成足够数量的数据用于神经网络的训练。在这片文章中还占相当大的篇幅，下面这张图右下角是生成的伪数据，左上角是真实数据。
在实验的设置中，D2D_2D2​的规模大概是D1D_1D1​的100倍。

最后的实验结果中有一些有趣的现象，第一点是，用人工数据集D2D_2D2​训练出的神经网络S1S_1S1​要比用原始数据D1D_1D1​训练出来的模型S1S_1S1​要好，第二点是S1S_1S1​的表现有时候会比原始的集成模型TTT更好，作者认为这可能是因为原始模型TTT过拟合了。

Do Deep Nets Really Need to be Deep?

先记录两个之前看到的结论，可能能更好地理解为什么作者要写这篇文章，

年就已经证明单层的神经网络只要够宽，再加上一个非线性映射，就足以模拟任何连续函数。 CS231n上曾经讲过为什么神经网络需要更深：浅的神经网络往往拥有更少的局部最优点，SGD在浅的神经网络上会更容易收敛到这些局部最优点，但浅网络的局部最优点loss都比较高。深的神经网络拥有更多的局部最优点，这些局部最优点的loss相对而言要低一些。因此浅的神经网络训练loss往往多变，深的神经网络训练结果比较一致也比较好。 还有一个解释是，神经网络本质是表示学习，深的神经网络能够通过层与层之间的变化表达出更复杂的特性

所以神经网络需要更深的目的更多的是，方便我们找到那个想找的函数。
那么，有没有什么办法，我们可以再在一个浅的神经网络上面，也找到我们想要的那个函数呢，注意这篇论文比较的是深和浅，所以做对照实验的时候，参数规模是要保持一致的。

为了验证这个结论，作者提出了一个算法尝试让浅的模型去学习深的模型的logits，损失函数为L2loss。logits是神经网络最后一层softmax层的输入。

用训练数据DDD训练一个深的神经网络TTT 用浅的神经网络SSS学习TTT在数据DDD上的logits

有两个点需要记录一下

为什么是学习logits而不是学习softmax输出的概率呢？作者的解释是模型最后的概率输出往往差距很大，类似[2e−9,4e−5,0.9999]这样的输出基本可以等同于one-hot标签了，本来学习大模型的目的就是希望大模型能给小模型的训练提供hint，要是直接学习概率输出，还不如干脆学习原始数据的one-hot标签算了。
（在之后的知识蒸馏开山论文中，Hinton 用temperature 的思想解决了这个问题。） 训练的过程中还用到了一个加速训练的方法，把H∗DH*DH∗D的全连接层分解成H∗k,k∗DH*k, k*DH∗k,k∗D两个全连接层，其中k≪H，Dk \ll H，Dk≪H，D，这是模型压缩方法中的低秩近似。

最后得到的结果是，浅层的神经网络有良好的大模型指导的的情况下，可以获得与同等参数数量的深层网络相似的性能。其次，如果直接用训练数据去训练浅层模型却无法获得等同的效果，这可能是由于相对于one-hot的label, logits能提供更多的信息。这还说明我们当前的优化算法不够好，在浅层神经网络情况下很难将loss降下去。

我的猜测

已经训练好的神经网络是见过所有的训练数据的，深层网络的logits蕴藏着所有训练数据的信息，而sgd毕竟每次只采样一部分数据，容易走偏路，如果做一个对比试验，使用gd而不是sgd去优化浅层网络，可能会有所发现。

Distilling the Knowledge in a Neural Network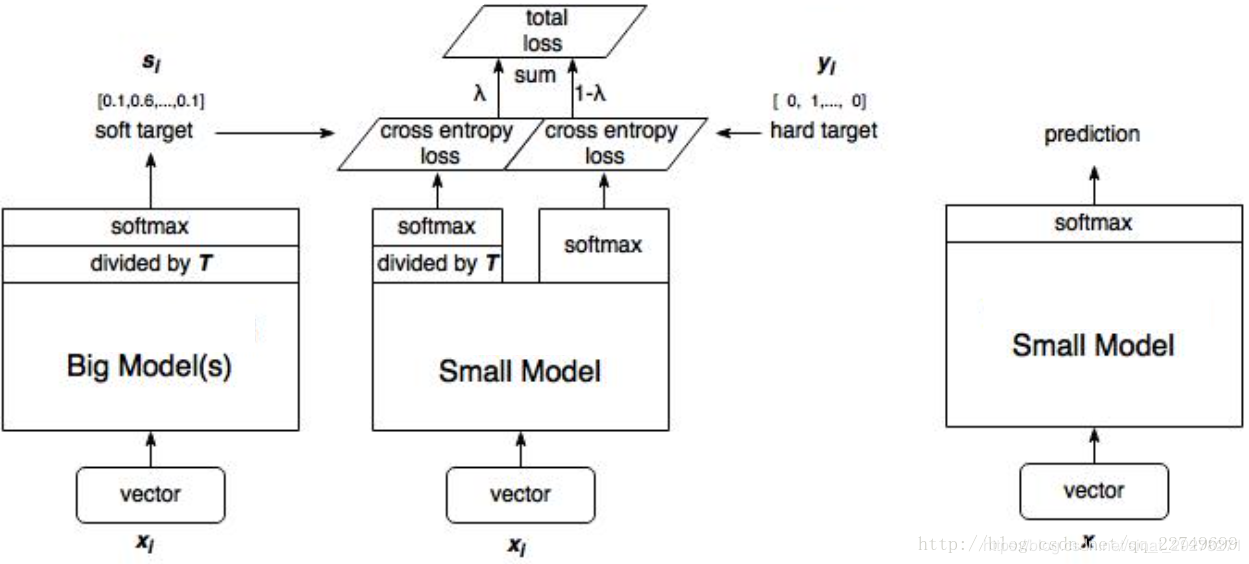

这篇文章就是知识蒸馏的开山之作了，思路可以用上面这张图讲清楚。

而且这篇文章解决了“Do Deep Nets Really Need to be Deep?”中，无法直接用softmax的输出值进行训练的问题。通过引入温度参数TTT，qi=exp(zi/T)∑jexp(zj/T)q_{i}=\frac {exp({z_i}/{T})}{\sum_jexp(z_j/T)}qi​=∑j​exp(zj​/T)exp(zi​/T)​软化softmax的输出，使得模型可以直接学习softmax的输出。同时作者也在论文中证明了，学习logits是参数T的一个特殊情况。可以说，这一步，是在学习logits和学习概率直接做了一个trade-off。这样想一想的话，你要不要在训练的过程中顺便调节一下温度，就像模拟退火算法那样。

算法的过程如下

先用hard target，也就是训练数据训练老师模型TTT。 利用训练好的TTT来计算soft target，也就是“软化后”的softmax输出。 训练小模型，在小模型与hard label的损失函数L1L_1L1​之外再加一个额外的soft target的损失函数L2L_2L2​，最终的损失函数L=L1+λL2L = L_1+\lambda L_2L=L1​+λL2​。λ\lambdaλ可以调节两个损失函数的权重。
作者：Uncle_Sugar

读书