数字滤波器matlab与FPGA实现读书笔记(三)FIR滤波器matlab和VHDL实现
FIR滤波器的FPGA实现
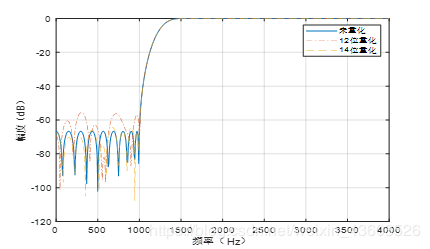
ex:设计一个高通最优FIR滤波器,过渡带为1000~1500Hz,采样频率为8000Hz,通带纹波最大为0.01,阻带纹波最大为0.001绘制比较系数12位、14位量化以及无量化是的幅度响应曲线,将14位量化结果转换成十六进制补码格式,并将14位量化的十进制存放在文本文件中。
设计一个对纹波及截至频率有确定要求的滤波器,需要使用firpm函数设计最优滤波器。而firpm函数无法确定滤波器的阶数,因此需要使用kaiserord函数先求取满足设计需求的最小滤波器阶数。
matlab行结果如图
2.1串行结构的FIR滤波器实现
滤波器实际上就是一个乘累加运算,且乘累加运算的次数还是由滤波器的阶数来决定。由于FIR滤波器大多是具有线性相位的滤波器,也就是说滤波器系数均呈一定的对称性。
所谓串行结构,即串行实现滤波器的累加运算,将每级延时单元与相应系数的乘积结果进行累加后输出,因此整个滤波器实际上只需要一个乘法器运算单元。串行结构还可分为全串行及半串行结构。全串行结构是指进行对称系数的加法运算也由一个加法器串行实现,半串行结构则指用多个加法器同时实现对称系数的加法运算。两种串行结构实现FIR滤波器的结构图如图1和图2所示
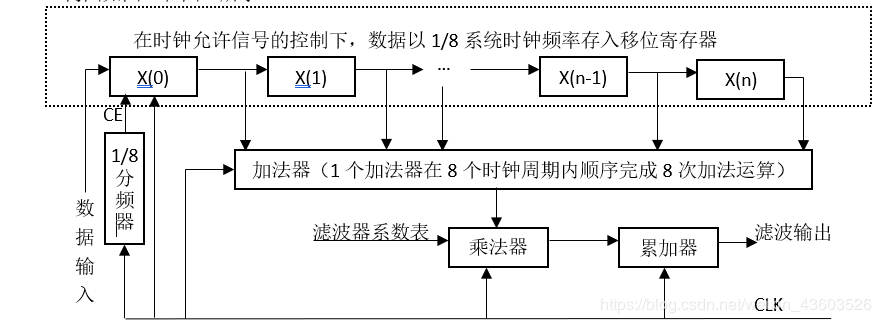
图1 具有线性相位的全串行FIR滤波器结构
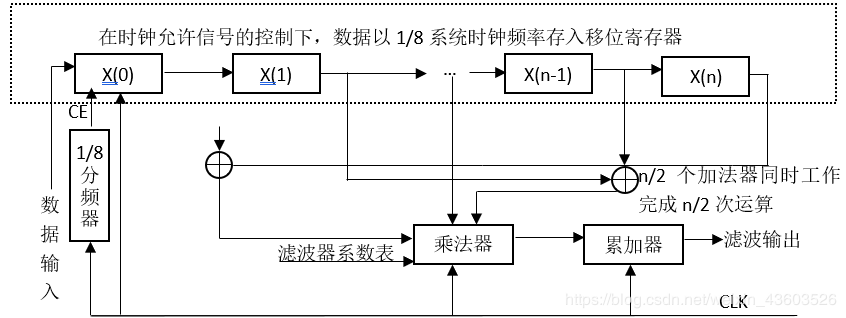
图2 具有线性相位的半串行FIR滤波器结构
两种结构的区别在于实现对称系数的加法运算实现方式。很明显,全串行结构利用更少的激发器资源
例:设计一个15阶(长度为16)的低通线性相位FIR滤波器,采用布莱克曼窗函数设计,截至频率为500Hz,采样频率为2000Hz;采用FPGA实现全串行结构的滤波器,系数的量化位数为23比特,输入数据位宽为12比特,输出的数据位宽为29比特,系统时钟为16kHz。
设计思路:首先采用MATLAB软件根据要求设计出滤波器的系数,并仿真出系数量化前后的幅频响应图;根据图4-18所示的结构采用VHDL语言在FPGA中实现滤波器;采用MATLAB软件仿真出具有白噪声特性的输入信号,以及由200Hz及800Hz单点频信号叠加的输入信号;采用MATLAB软件分析滤波器输出信号,比较输入/输出信号的时域及频域图。
第一步:用matlab软件设计出滤波器系数。
第二步:用matlab软件仿真滤波器测试数据、仿真测试数据经滤波器滤波后的输出数据,以便与FPGA程序实现后的结果进行比较,并判断FPGA程序实现的正确性。首先需要仿真生成12比特量化的采样频率为2000Hz的高斯白噪声、两个频率分别为200Hz与800Hz信号的合成信号,并将仿真的数据转换成二进制数据写入文本文件种,供FPGA仿真程序读取;然后,仿真出量化后的数据经滤波器滤波后的输出结果。
第三步:采用VHDL语言设计串行结构的FIR滤波器。
第四步:编写VHDL测试激励文件,在测试激励文件中设置时钟信号频率
第五步:运行Modelsim仿真软件对FPGA程序进行功能及时许仿真
第六步:编写MATLAB程序,从Modelsim仿真软件生成的文本文件种读取滤波器输出数据,对数据进行时域及频域分析。
2.2 FPGA并行结构的FIR滤波器
所谓并行结构,即并行实现滤波器的累加运算,具体来讲,即并行将对称系数的输入数据进行相加,而后采用多个乘法器并行实现系数与数据的乘法运算,最后将所有乘积结果相加输出。毫无疑问,这种结构具有最高的运行速度,由于不需要累加运算, 因此系数时钟频率可以与数据输出时钟频率一致。
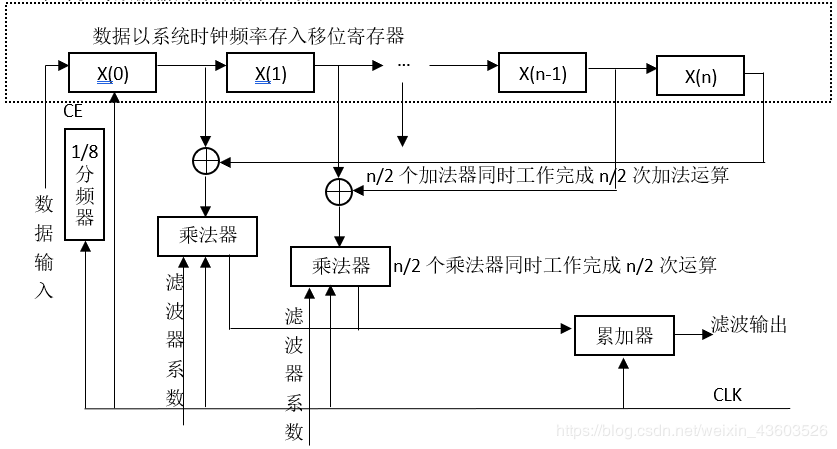
具有线性相位的并行FIR滤波器结构
2.3分布式结构的FPGA
分布式算法是一种专门针对乘加运算的运算方法。因此,严格来讲,分布式算法并不是针对FIR滤波器的算法,只是FIR滤波器的本质上刚好就是一个标准的乘加运算,分布式算法就正好在FIR滤波器设计中大有用武之地。
与传统算法相比,分布式算法可极大地减少硬件电路规模,很容易实现流水线处理,提高电路的执行速度,也就是提高系统运算速度
所谓分布式算法,就是指在完成乘加功能时通过将各输入数据每一对应位产生的结果预先进行相加形成相应的部分积,然后再对各部分积进行累加形成最终结果;而传统算法则是等到所有乘积结果产生后再进行相加,从而完成整个乘加运算。需要说明的是分布式算法应用的一个限定条件在于,每个乘法运算中必须有一个乘数为常数。
作者:久伴一生