《走近分形与混沌》读书笔记(part12)--随机过程与混沌

我们所说的混沌现象的确并不完全等同于随机，但是和随机过程有关系，它是随机过程和决定规律的结合。洛伦茨方程产生的混沌，显然不同于三体问题产生的混沌，它们有不同形态的奇异吸引子，分别作为它们各自的标签！这些奇异吸引子对应于不同的分形，分形有决定的一面，也有其随机的一面。

在这里，我们玩一个混沌游戏，使分形从随机过程中产生。

总结我们迄今为止所介绍过的分形，大概有如下三类：

1．科赫曲线、谢尔宾斯基三角形、分形龙等，可以从线性迭代过程产生；

2．曼德勃罗集、朱利亚集，从非线性复数迭代过程产生；

3．奇异吸引子，由洛伦茨方程或三体运动方程等非线性微分方程组产生。

我们都知道，谢尔宾斯基三角形可以用两种不同的方法产生。第一种方法就是如下图所示那样，将第一个涂黑的三角形挖掉它中心的三角形，成为第二个图，然后再继续挖下去…

第二种方法就是，从下图最左边的一个曲线开始迭代，迭代无限次之后，最后也得到谢尔宾斯基三角形。

现在我们通过混沌游戏，即随机过程的方式，得到谢尔宾斯基三角形：

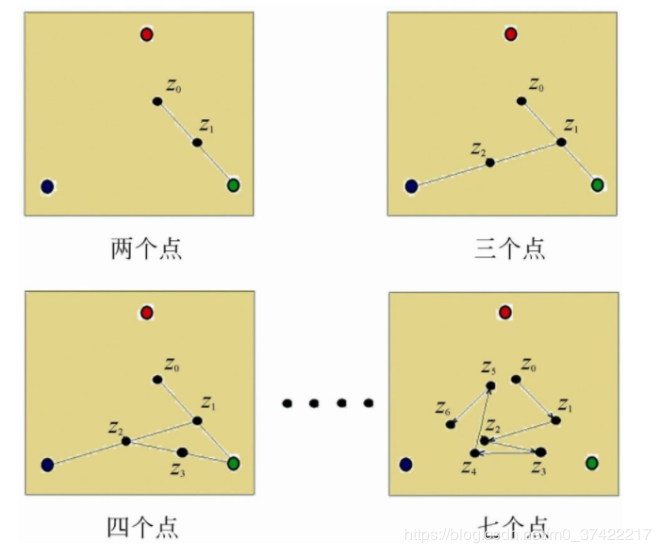
在左上角的初始图形上，画上红、绿、蓝三个顶点，并随意选择起始点Z0Z_0Z0​，再准备一个能随机产生红、绿、蓝之一的随机发生器。从Z0Z_0Z0​开始，利用随机选出的颜色点(这时是绿色)，取Z0Z_0Z0​到绿点的中点，作为下一个点Z1Z_1Z1​，然后，又利用再次随机选出的颜色点(这时是蓝色)，取Z1Z_1Z1​到蓝点的中点，作为Z2Z_2Z2​，以此往复地做下去，得到Z3,Z4,Z5...Z_3, Z_4, Z_5...Z3​,Z4​,Z5​...当我们得到的点足够多时，就构成了谢尔宾斯基三角形：

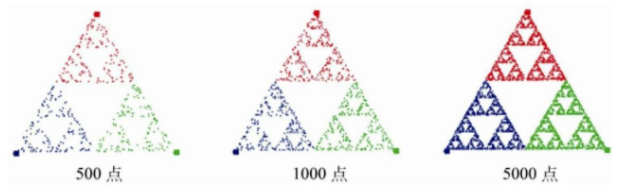
通过随机过程产生谢尔宾斯基三角形的过程，我们发现：看起来混沌，本质上却和迭代的效果是一样的。

那么除了谢尔宾斯基三角形，一般分形是否可以由混沌游戏产生？

产生分形所用的迭代方法，可以抽象成一组收缩变换函数，数学家们将此称为迭代函数系统(IFS)。任何分形，只要找到了对应的IFS，就能用迭代法(或者是混沌游戏的方法)产生出来，非线性的情况也一样。比如下面公式即为谢尔宾斯基三角形的IFS:
f1(z)=z/2f2(z)=z/2+1/2f3(z)=z/2+(3+1)/2 f_1(z)=z/2 \\f_2(z)=z/2 +1/2 \\f_3(z)=z/2 + (\sqrt{3} + 1)/2 f1​(z)=z/2f2​(z)=z/2+1/2f3​(z)=z/2+(3​+1)/2

随机过程 part 读书