随机过程基础(7)

Winona ·

更新时间:2024-09-21

· 795 次阅读

目录互功率谱非平稳过程的功率谱广义功率谱密度时变功率谱例子matlab互相关函数估计matlab功率谱估计例子：数字图像直方图随机过程应用：判断说话中的清音浊音归一化自协方差 互功率谱

类似从自相关函数推出互相关函数，也可以从单个随机过程的功率谱推出互功率谱。两个随机过程X(t)和Y(t)，它们的互功率谱定义是
GXY(ω)=E[lim⁡T→∞12TXT(ω)YT∗(ω)]G_{XY}(\omega)=E[\lim_{T\rightarrow \infty}\frac{1}{2T}X_T(\omega)Y_T^*(\omega)]GXY(ω)=E[T→∞lim2T1XT(ω)YT∗(ω)]
XT(ω)=∫−TTX(t)e−jωtdtX_T(\omega)=\int_{-T}^TX(t)e^{-j\omega t}dtXT(ω)=∫−TTX(t)e−jωtdt
YT(ω)=∫−TTY(t)e−jωtdtY_T(\omega)=\int_{-T}^TY(t)e^{-j\omega t}dtYT(ω)=∫−TTY(t)e−jωtdt
如果X(t)和Y(t)是联合平稳的，则RXY(τ)R_{XY}(\tau)RXY(τ)绝对可积。则它们的互功率谱和互相关函数是一对傅里叶变换对：
GXY(ω)=∫−∞inftyRXY(τ)e−jωτdτG_{XY}(\omega)=\int_{-\infty}^{infty}R_{XY}(\tau)e^{-j\omega \tau}d\tauGXY(ω)=∫−∞inftyRXY(τ)e−jωτdτ
RXY(τ)=12π∫−∞∞GXY(ω)ejωτdωR_{XY}(\tau)=\frac{1}{2\pi}\int_{-\infty}^{\infty}G_{XY}(\omega)e^{j\omega \tau}d\omegaRXY(τ)=2π1∫−∞∞GXY(ω)ejωτdω
互功率谱的性质：
GXY(ω)=GYX∗(ω)G_{XY}(\omega)=G_{YX}^*(\omega)GXY(ω)=GYX∗(ω)
∣GXY(ω)∣2≤GX(ω)GY(ω)|G_{XY}(\omega)|^2\le G_X(\omega)G_Y(\omega)∣GXY(ω)∣2≤GX(ω)GY(ω)

非平稳过程的功率谱 广义功率谱密度

设非平稳随机过程X(t)的自相关函数RX（t1,t2)是两个时间点的函数，则RX(t1,t2)R_X(t_1,t_2)RX(t1,t2)的二维傅里叶变换
GX(ω1,ω2)=∫−∞+∞∫−∞+∞RX(t1,t2)e−j(ω2t1−ω2t2)dt1dt2G_X(\omega_1,\omega_2)=\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}R_X(t_1,t_2)e^{-j(\omega_2t_1-\omega_2t_2)}dt_1dt_2GX(ω1,ω2)=∫−∞+∞∫−∞+∞RX(t1,t2)e−j(ω2t1−ω2t2)dt1dt2
为X(t)的广义功率谱密度，逆变换为
RX(t1,t2)=14π2∫−∞+∞∫−∞+∞GX(ω1,ω2)ej(ω1t1−ω2t2)dω1dω2R_X(t_1,t_2)=\frac{1}{4\pi^2}\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}G_X(\omega_1,\omega_2)e^{j(\omega_1t_1-\omega_2t_2)}d\omega_1d\omega_2RX(t1,t2)=4π21∫−∞+∞∫−∞+∞GX(ω1,ω2)ej(ω1t1−ω2t2)dω1dω2
广义谱的定义在数学上与平稳随机过程是相通的。假设GX(ω1,ω2)G_X(\omega_1,\omega_2)GX(ω1,ω2)仅在两者相等处有值，两者不等时的结果是0，则
GX(ω1,ω2)=GX(ω1)δ(ω1−ω2)G_X(\omega_1,\omega_2)=G_X(\omega_1)\delta (\omega_1-\omega_2)GX(ω1,ω2)=GX(ω1)δ(ω1−ω2)这就是平稳情况下的功率谱。

时变功率谱

假设t1=t,t2=t+τ，则非平稳过程的自相关函数
RX(t+τ,t)=RX(t,τ)=E[X(t+τ)X(t)]R_X(t+\tau,t)=R_X(t,\tau)=E[X(t+\tau)X(t)]RX(t+τ,t)=RX(t,τ)=E[X(t+τ)X(t)]
是t和τ\tauτ的函数，时变谱定义成
GX(t,ω)=∫−∞∞RX(t,τ)e−jωτdτG_X(t,\omega)=\int_{-\infty}^{\infty}R_X(t,\tau)e^{-j\omega \tau}d\tauGX(t,ω)=∫−∞∞RX(t,τ)e−jωτdτ
如果采用对称相关函数
RX(t,τ)=E[X(t+τ/2)X(t−τ/2)]R_X(t,\tau)=E[X(t+\tau/2)X(t-\tau/2)]RX(t,τ)=E[X(t+τ/2)X(t−τ/2)]
则这种时变谱称为维格纳-威利谱（WV谱）其中，GX(t,ω)=∫−∞∞RX(t,τ)e−jωτdτG_X(t,\omega)=\int_{-\infty}^{\infty}R_X(t,\tau)e^{-j\omega \tau}d\tauGX(t,ω)=∫−∞∞RX(t,τ)e−jωτdτ还可以写成
GX(t,ω)=E[WX(t,ω)]G_X(t,\omega)=E[W_X(t,\omega)]GX(t,ω)=E[WX(t,ω)]
其中
WX(t,ω)=∫−∞∞[X(t+τ/2)X(t−τ/2)]e−jωτdτW_X(t,\omega)=\int_{-\infty}^{\infty}[X(t+\tau/2)X(t-\tau/2)]e^{-j\omega \tau}d\tauWX(t,ω)=∫−∞∞[X(t+τ/2)X(t−τ/2)]e−jωτdτ
WX(t,ω)W_X(t,\omega)WX(t,ω)称为维格纳分布，非平稳随机过程X(t)的WV时变谱是该过程维格纳分布的数学期望。

例子

设噪声调制的振荡信号
X(t)=N(t)cosω0tX(t)=N(t)cos\omega_0tX(t)=N(t)cosω0t其中N(t)是平稳噪声，求X(t)的功率谱。
观察这个信号，发现不同时刻的信号（可能的）均值受到了三角函数的调制。X(t)是非平稳随机过程。求功率谱的方法一般就是求相关函数的傅里叶变换，而对于非平稳过程，有广义功率谱密度、时变功率谱等表示形式，但最常用的还是对即时相关函数做时间平均，然后进行傅里叶变换，如下。
RX(τ,t)=12RN(τ)[cosω0(2t+τ)+cosω0τ]R_X(\tau,t)=\frac{1}{2}R_N(\tau)[cos\omega_0(2t+\tau)+cos\omega_0\tau]RX(τ,t)=21RN(τ)[cosω0(2t+τ)+cosω0τ]
所谓的对时间函数求平均，指的是
RX(τ)‾=lim⁡T→∞12T∫−TT12RN(τ)[cosω0(2t+τ)+cosω0τ]dt\overline {R_X(\tau)}=\lim_{T\rightarrow\infty}\frac{1}{2T}\int_{-T}^{T}\frac{1}{2}R_N(\tau)[cos\omega_0(2t+\tau)+cos\omega_0\tau]dtRX(τ)=T→∞lim2T1∫−TT21RN(τ)[cosω0(2t+τ)+cosω0τ]dt=12RN(τ)cosω0τ=\frac{1}{2}R_N(\tau)cos\omega_0\tau=21RN(τ)cosω0τ
对上述自相关函数求时间平均就得到了结果：
GX(ω)=14[GN(ω+ω0)+GN(ω−ω0)]G_X(\omega)=\frac{1}{4}[G_N(\omega+\omega_0)+G_N(\omega-\omega_0)]GX(ω)=41[GN(ω+ω0)+GN(ω−ω0)]

matlab互相关函数估计

参见文档https://www.mathworks.com/help/matlab/ref/xcorr.html

>> a=0.8;
>> sigma=2;
>> N=500;
>> u=randn(N,1);
>> x(1)=sigma*u(1)/sqrt(1-a^2);
>> for i=2:N
x(i)=a*x(i-1)+sigma*u(i);
end
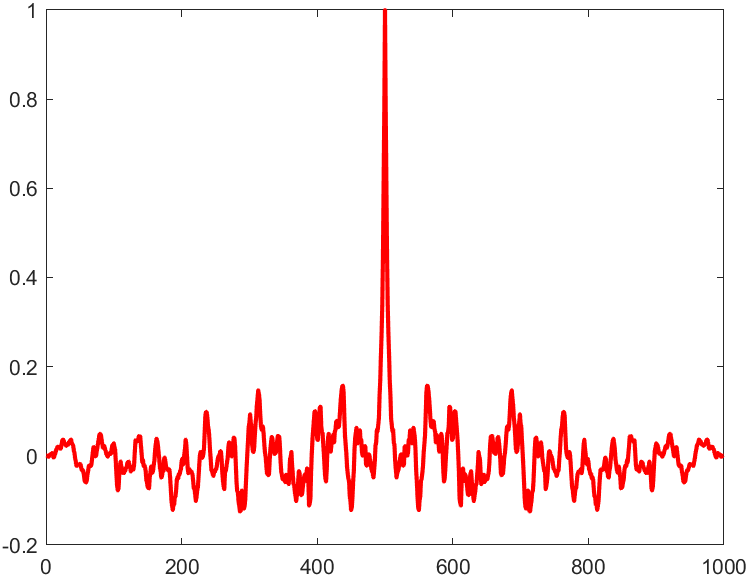
>> R=xcorr(x,'coeff');
>> plot(R,'r','linewidth',2);

原创文章 30获赞 12访问量 5193 关注私信展开阅读全文
作者：粽子哥哥123