随机过程的理解

随机过程的理解随机变量分布函数期望相关性方差抽样随机过程稳态自相关函数其他解释参考 一个六面的骰子,每一面都是一个确定的实数,每次投骰子的结果都是一个确定的实数,可以把该骰子视为随机变量,每次投骰子都的结果都对应一个随机变量的取值. 一个六面的骰子,每一面都是一个函数,每次投骰子的结果都是一个确定的函数,可以把该骰子视为随机过程,每一时刻投骰子的结果都是一个确定的函数(随机变量). 随机变量 一个实验可能出现的结果的集合 一个实验的可能性 分布函数 横坐标视为实验(随机变量),每个值表示实验结果(随机变量的取值),纵左边为每个实验结果发生的概率. 随机变量的结果虽然是一个确定的数,如{1,2,3,…},但可以表示的是一段时间,二段时间,三段时间…等. 期望 对一个随机变量，已知其分布函数，可以定义一个期望。这个东西由每个结果的取值(横坐标)和它的可能性(纵坐标)共同决定，表达未来结果的加权平均值。 相关性 对于两个随机变量，描述一个随机变量随另一个而变化的趋势.它是现实生活中我们说两个事物相关性的精确表达. 方差 实验结果(随机变量)距离均值(期望)的偏差程度. 抽样 抽样就是已知分布函数取得一个随机的结果的过程. 随机过程 确定性过程研究一个量随时间确定的变化,而随机过程描述的是一个量随时间可能的变化,在这个过程里,每一个时刻变化的方向都是不确定的,或者说随机过程就是由一系列随机变量组成,每一个时刻系统的状态都由一个随机变量表述,而整个过程则构成态空间的一个轨迹(随机过程的实现). 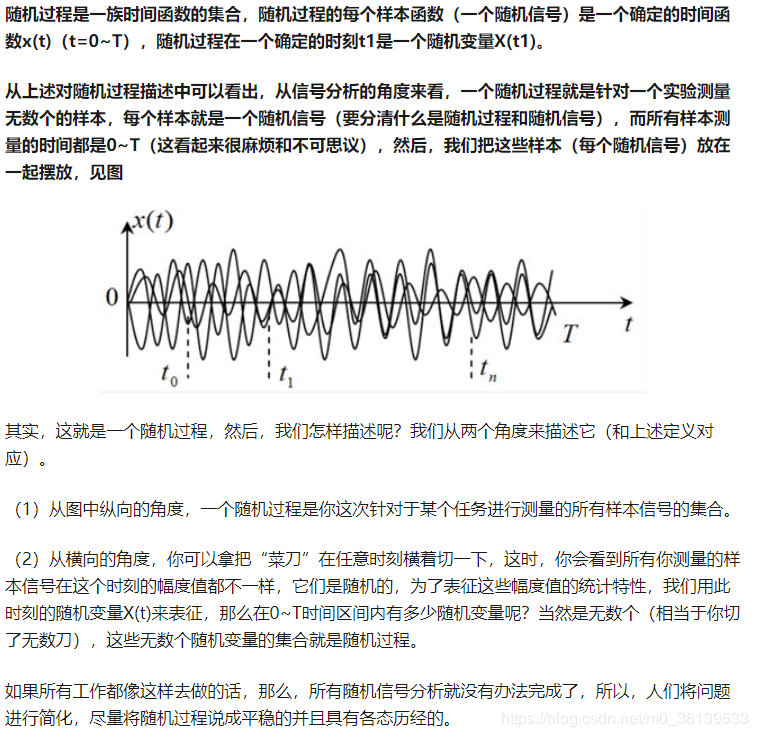随机过程横坐标为时间,纵坐标为实验结果(随机变量),即同一时刻可能得到不同的实验结果(随机变量). 可以理解为x坐标为时间,y坐标为随机变量,z坐标为随机变量的概率分布. 稳态 稳态的含义正是在平均值附近扰动 计算方差,来看扰动的剧烈程度. 自相关函数 它描述的就是此时的扰动和彼时的扰动的相关性.
其他解释

参考

链接: 参考.

作者：夜雪-初霁

随机过程