【论文笔记】Highway Network: Training Very Deep Networks (2015)

Adeline ·

更新时间:2024-11-10

· 838 次阅读

这篇论文提出了著名的Highway Network，用于解决深层网络的训练问题。这个结构已经得到了广泛的应用，也有很多资料。我之所以阅读这篇五年前的论文，主要是看现在的资料觉得对网络的结构理解的还是比较浅，于是想看看发明者的思路，在这里对收获做了一些总结。

1.介绍

网络深度的增加会为网络带来更多的表现力，但网络深度同时也让网络很难去训练。在这篇论文之前，解决方案大致从这几个方面出发：

优化器： Training deep and recurrent networks with hessian-free optimization On the importance of initialization and momentum in deep learning Identifying and attacking the saddle point problem in high-dimensional non-convex optimization 初始化策略 Understanding the difficulty of training deep feedforward neural networks Delving deep into rectifiers: Surpassing human-level performance on ImageNet classification 激活函数 Maxout networks. Compete to compute 层之间的Skip connections Deep learning made easier by linear transformations inperceptrons Generating sequences with recurrent neural networks

另外还有一种很清奇的思路，是用一些浅层网络（称为教师网络）来分阶段地辅助训练更深的学生网络（ FitNets: Hints for thin deep nets）。学生网络去预测教师网络的参数。但这样的设计毕竟不如直接训练。

2. 模型和实验

作者从LSTM得到启发，发明了Highway Network。

在普通（plain）前馈网络中，一个典型的层结构(block)是：
y=H(x,WH)y = H(x, W_H)y=H(x,WH)
意为在参数WHW_HWH参与下进行非线性变化HHH。

而在Highway Network中，模型被定义如下：
y=H(x,WH)⋅T(x,WT)+x⋅C(x,WC)y=H(x,W_H)·T(x,W_T)+x·C(x, W_C)y=H(x,WH)⋅T(x,WT)+x⋅C(x,WC)
其中(⋅)(·)(⋅)是按位乘法(element-wise multiplication)。与上面不同，这个结构的输出信息不仅包括经过转换的信息H(x,WH)H(x,W_H)H(x,WH)，还包括原输入xxx。

而新引入了两个值，TTT（transform gate, 转换门）和CCC（carry gate, 携带门）的值定义了两道“门”，他们决定了这两部分在总输出中占有多大比例。这两部分也通过xxx的非线性变换得到。

为了简化，一般设置C=1−TC=1-TC=1−T，这就得出：
y=H(x,WH)⋅T(x,WT)+x⋅(1−T(x,WT))y=H(x,W_H)·T(x,W_T)+x·(1-T(x,W_T))y=H(x,WH)⋅T(x,WT)+x⋅(1−T(x,WT))
因此，根据转换门的输出，highway 层就可以让行为从进行计算到直接穿过之间平滑地转换。

不难看出在这个模型里有一个限制，即输入和输出必须维度相同，论文中也给出了解决方案，即对x进行变化，比如当输出维度大于输入时，为xxx填0,；当输出小于输入维度，做xxx的上采样。

模型里省略了偏置，而在实际使用时，转换门 TTT 的偏置 bTb_TbT 的初始化对训练有一定影响。一般而言，当其他参数以0为均值正常初始化时，可以初始化为负数，例如-1,-3，当层数很多（指多个highway），应选用更小的值。

这样带来的影响是，初始时每个转换门都很小，这样信息更倾向于直接穿过，以此避免在一开始时由于陷入退化为普通深层网络而导致无法训练的情况。

在实际构建模型时，不只是全连接层可以Highway化，RNN，CNN一样可以。但LSTM不用，因为这本身就相当于一个简化的LSTM单元。

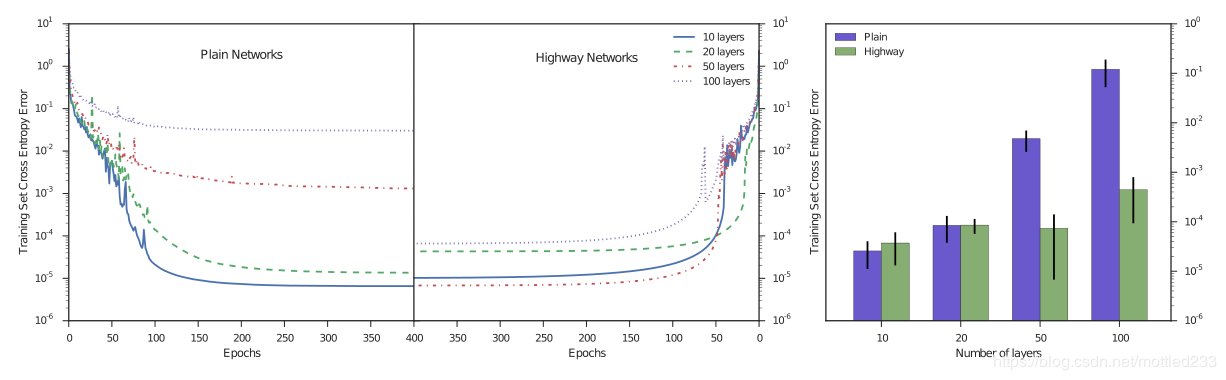
作者在MNIST和CIFAR上做了测试，在参数量相同的情况下，不同层数对训练的影响如下图：
在这里插入图片描述

3.分析

在这一部分，作者别出心裁地给出了下面的图对参数进行了可视化，这个图描述了在MNIST和CIFAR任务搭建的50层的Highway网络中，网络各部分的运行情况。
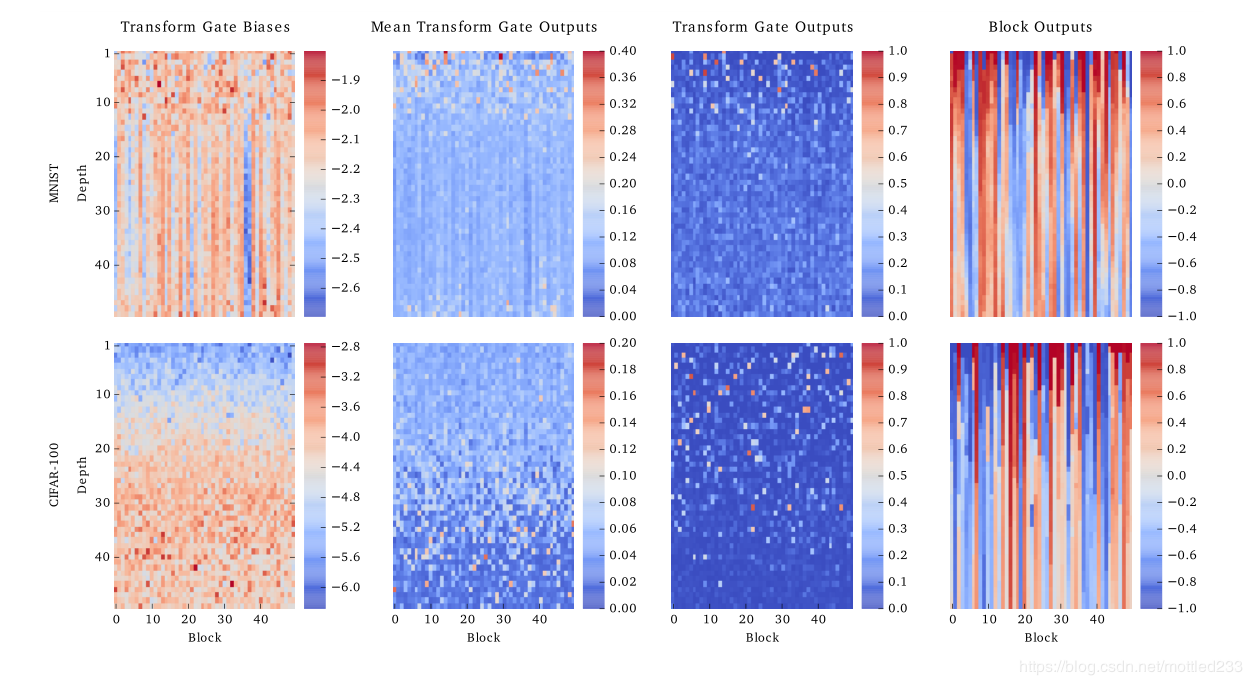
在这里插入图片描述
图片中，第一行是MNIST任务训练得到的网络，第二行是CIFAR任务中的网络。而按列，四张图分别代表：转换门的偏置，转换门的平均输出，单个随机样本的转换门输出，单个随机样本整个结构的输出。

其中每张图中，每一行代表一层网络，一层中的每一列代表对应的特征的值。

论文中，从图上得到值得关注的结论如下：

初始化时，两个网络的转换门偏置分别被赋值-2和-4，但从图上可以看出，在训练后大多数偏置值反而变得比最初还要低。在MNIST网络的第二张转换门的平均输出图中，可以看出转换门的输出显著集中于前15层。而在CIFAR网络的第一张和第二张图中，可以发现偏置随着层数增加而逐渐变大，但是与之相反，转换门输出随层数逐渐减小。这意味着更小的偏置并没有让这个门关闭，而是让它更有选择性。在第三张图中可以看出，实际上输出是较为稀疏的，这意味着对特征的选择性很强。第四张图便显出了“信息高速公路”的视觉化概念。大多数输出在多层上保持恒定，形成了条纹图案；而越接近下层，变化就越小。对于MNIST数据集，这些发生在约前15层，对CIFAR数据集主要发生在前40层。这是因为MNIST数据集简单，并不需要更为复杂的网络。这也说明Highway网络有能力判断网络的层数影响。

基于以上结论，特别是对第三条，作者分析Highway网络与传统的“硬连线”的跳跃连接相比，这种方式可以对根据输入的信息进行动态的路由。而从图中的转换门平均输出可以看出，这种能力是有着泛化性的，而不是只对训练集数据的一种静态路由。

而对第二条和第四条结论的推测进行验证，作者进行了消融分析，通过让一些层的转换门输出变为0，基本上等同于禁用这个层，查看禁用层对准确率的影响来判断层起到了多大的作用，得到了下图：
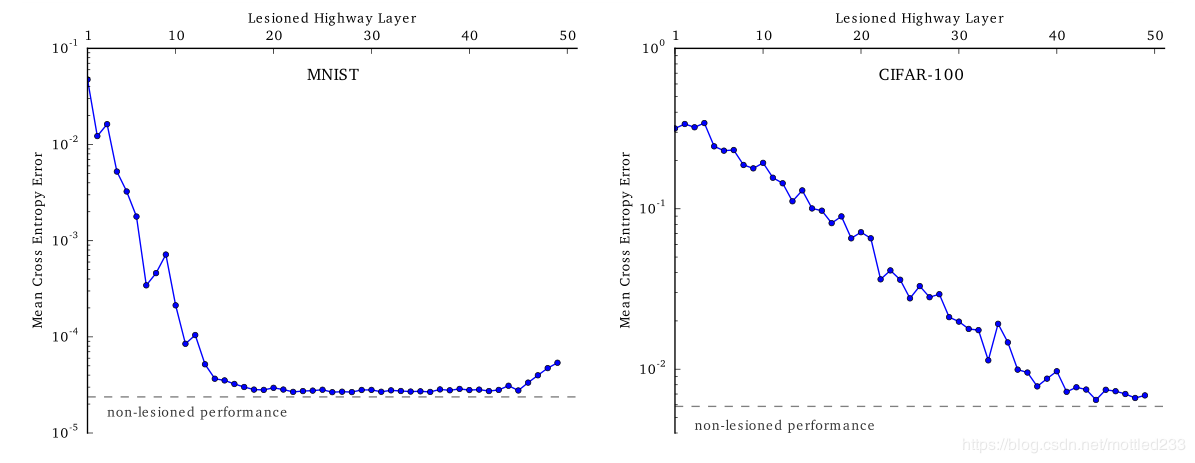
在这里插入图片描述
可以看出，在MNIST数据集中，前面的15层对结果影响尤为重要，而CIFAR数据集上野与结论类似。