混淆矩阵Confusion Matrix概念分析翻译

在机器学习领域，混淆矩阵（confusion matrix），又称为可能性表格或是错误矩阵。它是一种特定的矩阵用来呈现算法性能的可视化效果，通常是监督学习（非监督学习，通常用匹配矩阵：matching matrix）。

其每一列代表预测值，每一行代表的是实际的类别。这个名字来源于它可以非常容易的表明多个类别是否有混淆（也就是一个class被预测成另一个class）。

假设有一个用来对猫（cats）、狗（dogs）、兔子（rabbits）进行分类的系统，混淆矩阵就是为了进一步分析性能而对该算法测试结果做出的总结。假设总共有 27 只动物：8只猫， 6条狗， 13只兔子。结果的混淆矩阵如下图：

在这个混淆矩阵中，实际有 8只猫，但是系统将其中3只预测成了狗；对于 6条狗，其中有 1条被预测成了兔子，2条被预测成了猫。从混淆矩阵中我们可以看出系统对于区分猫和狗存在一些问题，但是区分兔子和其他动物的效果还是不错的。所有正确的预测结果都在对角线上，所以从混淆矩阵中可以很方便直观的看出哪里有错误，因为他们呈现在对角线外面。

在预测分析中，混淆表格（有时候也称为混淆矩阵），是由false positives，falsenegatives，true positives和true negatives组成的两行两列的表格。它允许我们做出更多的分析，而不仅仅是局限在正确率。准确率对于分类器的性能分析来说，并不是一个很好地衡量指标，因为如果数据集不平衡（每一类的数据样本数量相差太大），很可能会出现误导性的结果。例如，如果在一个数据集中有95只猫，但是只有5条狗，那么某些分类器很可能偏向于将所有的样本预测成猫。整体准确率为95%，但是实际上该分类器对猫的识别率是100%，而对狗的识别率是0%。

对于上面的混淆矩阵，其对应的对猫这个类别的混淆表格如下：

假定一个实验有 P个positive实例，在某些条件下有 N 个negative实例。那么上面这四个输出可以用下面的偶然性表格（或混淆矩阵）来表示：

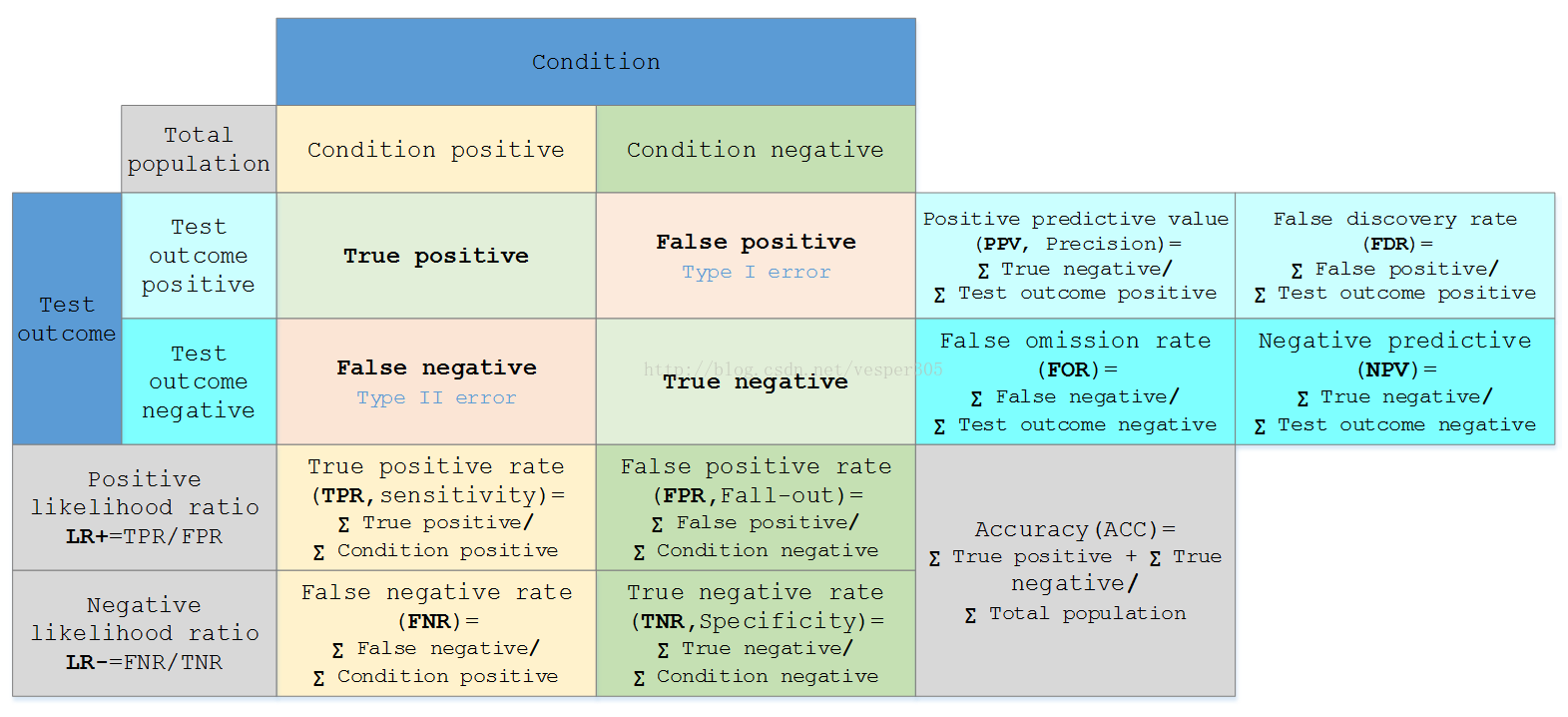
公式陈列、定义如下：

以上就是混淆矩阵Confusion Matrix分析翻译的详细内容，更多关于混淆矩阵Confusion Matrix的资料请关注软件开发网其它相关文章！

matrix