Codeforces 1316 D. Nash Matrix（dfs）

Grace ·

更新时间:2024-11-10

· 616 次阅读

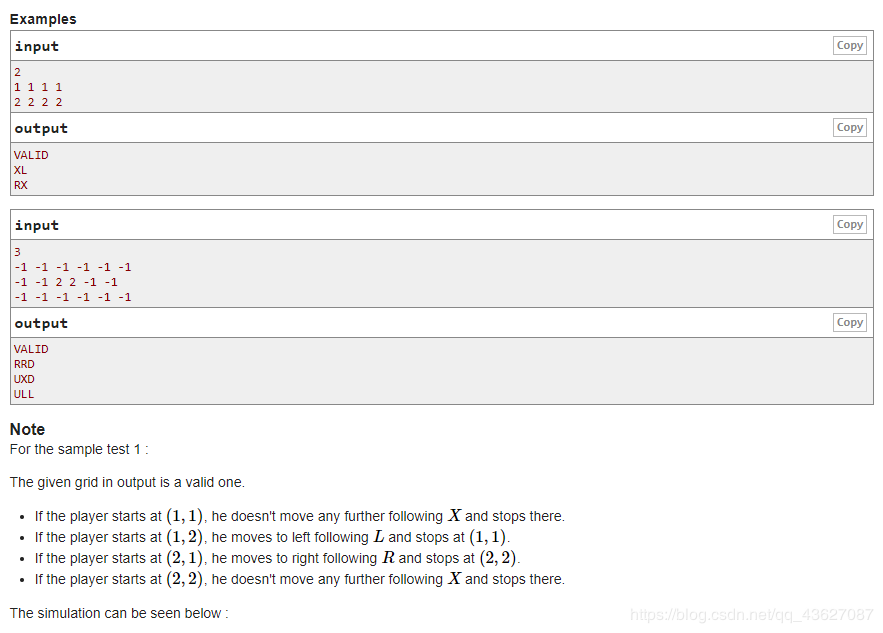
在这里插入图片描述

题意：

给出一个 n∗nn*nn∗n 的棋盘和每个棋盘位置最后能走到的位置，如果一直走不停下来就是 (−1,−1)(-1,-1)(−1,−1) ，可以停下来就是走到的最后位置，让你输出每个位置的操作字符，U,D,L,RU,D,L,RU,D,L,R上下左右和 XXX，停在此位置。

我们先找到所有可以停下的位置，那么这个位置的字符一定是
XXX，然后以这个位置为终点，方向搜索找到可以停在此位置的，搜索过程填上相反方向的字符即可。然后就是处理一直走不停的，找到一个走不停的格子，如果他相邻格子也是一直不停，就可以继续搜索下去。 AC代码：

const int N = 1e3 + 5;
struct node
{
    int x, y;
} a[N][N];
char g[N][N];
int n;
int mov[4][2] = {-1, 0, 1, 0, 0, -1, 0, 1};
char mc[4] = {'D', 'U', 'R', 'L'};  //反向
char mc2[4] = {'U', 'D', 'L', 'R'}; //正向
void dfs(int nx, int ny, int fx, int fy)
{
    rep(i, 0, 3)
    {
        int tx = nx + mov[i][0];
        int ty = ny + mov[i][1];
        if (tx  n || ty  n || g[tx][ty] != '0')
            continue;
        if (a[tx][ty].x == fx && a[tx][ty].y == fy)
        {
            g[tx][ty] = mc[i];
            //cout << tx << " " << ty << " " << g[tx][ty] << " " << fx << " " << fy << endl;
            dfs(tx, ty, fx, fy);
        }
    }
}
void init()
{
    rep(i, 1, n)
        rep(j, 1, n)
            g[i][j] = '0';
}
int main()
{
    sd(n);
    init();
    rep(i, 1, n)
        rep(j, 1, n)
            sdd(a[i][j].x, a[i][j].y);
    rep(i, 1, n)
    {
        rep(j, 1, n)
        {
            if (a[i][j].x == i && a[i][j].y == j)
            {
                g[i][j] = 'X';
                dfs(i, j, i, j);
            }
        }
    }
    rep(i, 1, n)
    {
        rep(j, 1, n)
        {
            if (a[i][j].x == -1 && a[i][j].y == -1 && g[i][j] == '0')//一直走循环的情况
            {
                bool flag = false;
                rep(k, 0, 3)
                {
                    int tx = i + mov[k][0];
                    int ty = j + mov[k][1];
                    if (tx  n || ty  n || g[tx][ty] != '0')
                        continue;
                    if (a[tx][ty].x == -1 && a[tx][ty].y == -1)//前一个位置也循环了
                    {
                        g[i][j] = mc2[k];
                        flag = true;
                        break;
                    }
                }
                if (flag)
                    dfs(i, j, -1, -1);
            }
        }
    }
    rep(i, 1, n)
    {
        rep(j, 1, n)
        {
            if (g[i][j] == '0')
            {
                puts("INVALID");
                return 0;
            }
        }
    }
    puts("VALID");
    rep(i, 1, n)
    {
        rep(j, 1, n)
            printf("%c", g[i][j]);
        puts("");
    }
    return 0;
}

作者：邵光亮

CodeForces dfs matrix

1024 个赞