图论——最短路径——Floyd算法的证明[1.0]
Floyd算法考虑的是一条最短路径上的中间结点。
什么是中间节点举个例子:
一个简单路径p = 上的中间结点指的就是除了v1和vl之外的任意节点, 也就是处于集合内的结点。
Floyd算法是解决多源最短路径的一个算法, 它可以允许存在负边, 但不允许存在负环路。
算法证明:假设图G的所有节点V = {1,2,…,n}, 考虑其中的子结点k是某个小于n的整数。对于任意一对结点i, j ∈ V, 考虑从节点i到j的路径, 其所有中间结点均取自集合{1,2,3…,k}, 并且设当前的最短路径为p。
Floyd算法利用的是已知p和 k = k-1时的关系(即{1,2,3…,k-1}时的关系), 判断k是否是路径p上的一个中间结点。
基于上面的观察, 我们可以定义一个最短路径估计的递归公式。设dkij为从结点i到结点j的所有中间结点全部取自集合{1,2,3,…,k}的一条最短路径。当k = 0时, 从结点i到结点j的最短路径是一条不包含编号大于0的路径(即没有任何中间结点)。 这样的路径最多只有一条边, 因此, d0ij = wij。 根据上面的讨论, 递归定义dkij如下:
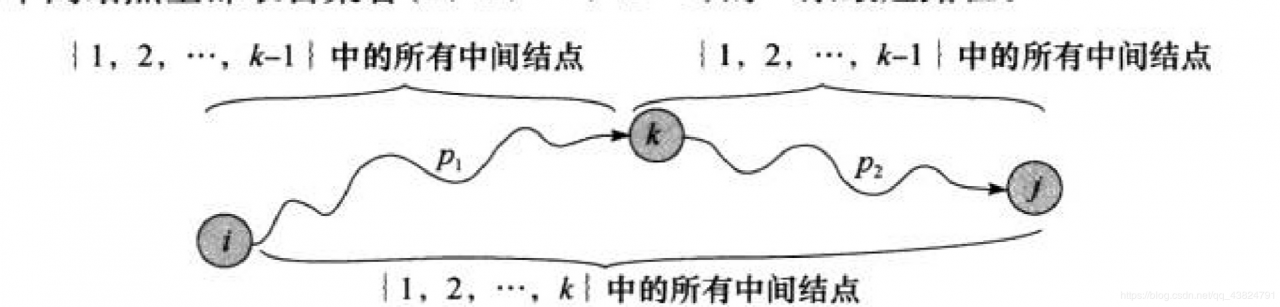
图1-1[来自算法导论]
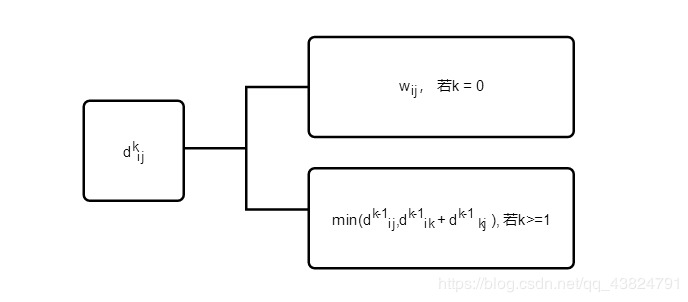
(公式25.5)
所以当k = n时, 就计算出了最终答案。
自底向上计算最短路径根据公式25.5,我们就可以使用自底向上的算法以递增次序计算dkij的值。
这个算法的实现, 就是我们常说的三个for循环
这只是我个人的一个实现, 相信大家还求更好的实现方式
for(k = 0;k < n;k++)
for(i = 0;i< n;i++)
for(j = 0;j grap[i][k]+grap[k][j])
grap[i][j] = grap[i][k]+grap[k][j];
引理24.1:
这一引理简单的说就是:
最短路径上的子路径也是最短路径。
具体内容如下:
(最短路径的子路径也是最短路径)
给定带权重的有向图G = (V,E)和权重函数wi, E→R,设p = 为从结点v0到结点vk的一条最短路径, 并且对于任意的i和j , 0<= i<=j <=k, 设pij = 为路径p从结点i到结点j的子路径,那么pij是从结点i到结点j的一条最短路径。
算法导论, 是从严谨证明的角度, 讲述算法一本书, 如果想要知道某些算法的更加严谨的证明过程, 算法导论是一本不错的书。
作者:Probie Tao