python3实现无权最短路径的方法
现有一个有向无权图。如下图所示:

问题:使用某个顶点s作为输入参数,找出从s到所有其他顶点的最短路径。
说明:因为是无权图,因此我们可以为每台边赋值为1。这里选择v3为s作为起点。
此时立刻可以说,从s到v3的最短路径是长为0的路径,标记此信息,得到下图。
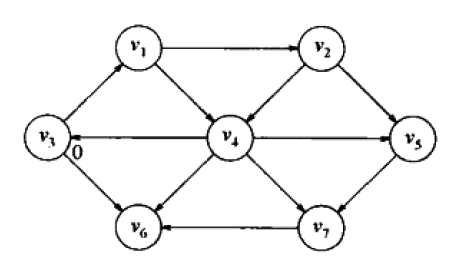
现在开始寻找从s出发距离为1的顶点。这些顶点肯定是与s邻接的顶点,很明显,v1,v6从s出发只需要一条边就到了。所以,从s出发距离为1的顶点,为v1,v6。
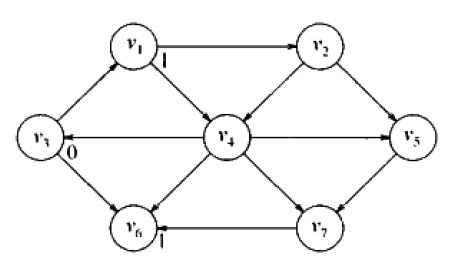
现在开始寻找从s出发距离为2的顶点。这些顶点肯定是与v1,v6(距离为1的顶点)邻接的顶点。发现与v1邻接的顶点为v2,v4,与v6邻接的顶点没有(不能往回走,没有出边)。所以,从s出发距离为2的顶点,为v2,v4。
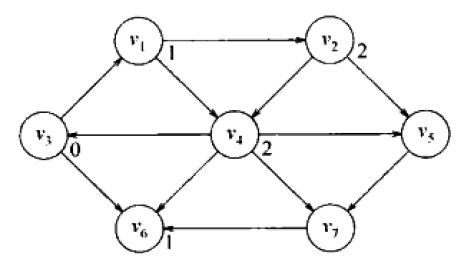
最后,考察与v2,v4邻接的顶点,即v5,v7。所以,从s出发距离为3的顶点,为v5,v7。
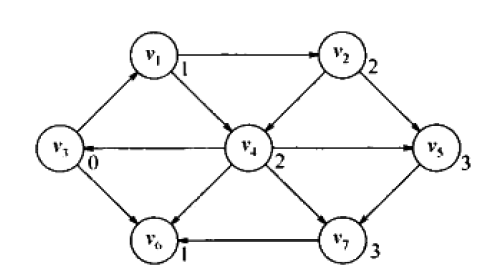
这种搜索图的方法称为广度优先搜索(breadth-first search)。按层处理顶点,距离起点近的顶点先处理,距离起点远的后处理。
伪代码(处理节点)
void unweighted(Vertex s){
Queue<Vertex> q = new Queue<Vertex>();
//把每个顶点的距离设为无穷大
for each Vertex v
v.dist = INFINITY
//将起点的距离设为0
s.dist = 0;
//起点入队,作为算法的开始
q.enqueue(s);
//只要队列不为空,便继续循环
while( !q.isEmpty() ){
//获得出队顶点
Vertex v = q.dequeue();
//对与v邻接的每个顶点进行处理
for each Vertex w adjacent to v
if(w.dist == INFINITY){
w.dist = v.dist + 1;
w.path = v;//代表w的上一个经过的顶点为v
//完成操作后,便入队,以用来接着分析与w邻接的顶点们
q.enqueue( w );
}
}
}
实现过程

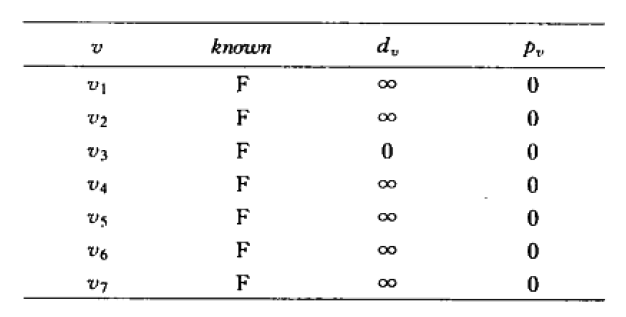
从s开始到顶点的距离放到dv列里,pv列用来代表,当前行代表的顶点的上一个经过的顶点。known列代表此顶点已经被处理过了。
初始化时,将起点的距离设置为0,且所有的顶点都不是know的。
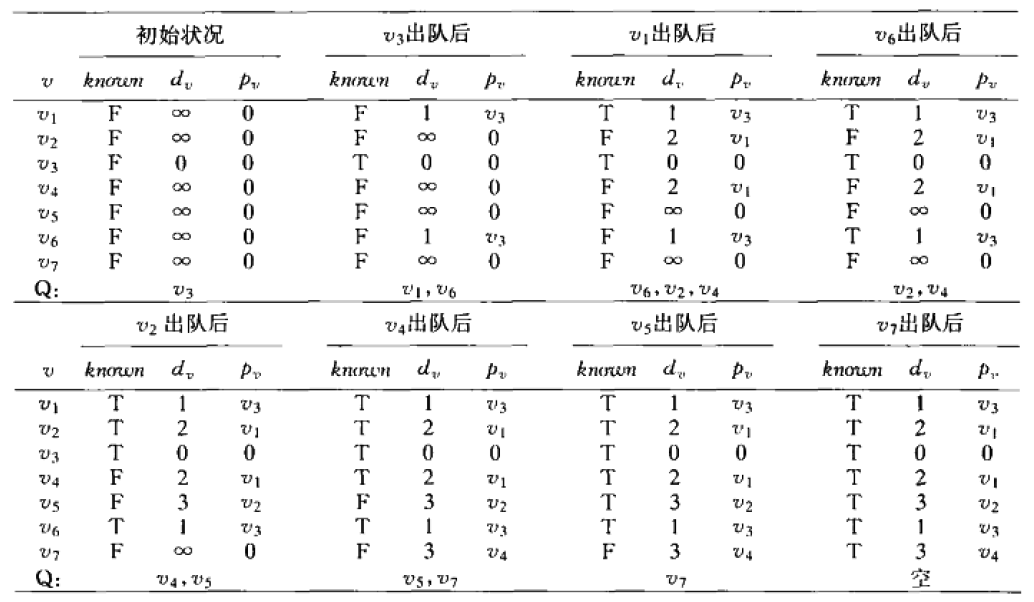
结合伪代码进行分析:
【1】当第一次循环中,出队的是v3(每次循环只出队一个顶点)
【2】而第一次循环结束时,就是上表中“v3出队后”的数据情况,如下
【3】此时,对v3的邻接的顶点们都作了处理,所以v3就从F变成了T(即已知)
【4】与v3邻接的顶点v1,v6都作了处理,dv都变成了1,pv都为v3
【5】而因为与v1,v6的邻接顶点都还没有开始处理呢,所以v1,v6的F还不能变成T
通过观察图,可以发现有两条路径长为3的最短路径。
【1】v3 => v1 => v2 => v5
【2】v3 => v1 => v4 => v7
我们可以通过数据变化表的最终情况来找到这两条路径。

注意,第一行代表v1,以此类推。
以找到v3 => v1 => v2 => v5路径为例,过程如下:
【1】找到距离为0的顶点,0在且只在第三行,所以第一个顶点为v3
【2】找到距离为1且pv为v3的顶点,有第一行和第六行,这里必须选一个,这里选第一行,所以第二个顶点为v1
【3】找到距离为2且pv为v1的顶点,有第二行和第四行,这里选第二行,所以第三个顶点为v2
【4】找到距离为3且pv为v2的顶点,只有第五行,所以第四个顶点为v5
【5】找到距离为4且pv为v5的顶点,没有,结束。
其实,以上步骤,是给出了,在对顶点进行数据处理后,找出无权最短路径的算法的思想。
其实可以,维护一些顶点间指针,用来指向下一个顶点,这样就可以用递归的思路来做,从起点开始,每递归到下一层距离dv便加1,用一个中间变量存储经过的顶点,每调用一次递归,便打印这个中间变量,这样,便能得到所有的无权最短路径。
这里得到无权最短路径的伪代码也不给出了,以上分析供大家理解参考。
纸上得来终觉浅,绝知此事要躬行!还是觉得用代码实现一遍比较好。
from queue import Queue
class Vertex:
#顶点类
def __init__(self,vid,outList):
self.vid = vid#出边
self.outList = outList#出边指向的顶点id的列表,也可以理解为邻接表
self.know = False#默认为假
self.dist = float('inf')#s到该点的距离,默认为无穷大
self.prev = 0#上一个顶点的id,默认为0
#创建顶点对象
v1=Vertex(1,[2,4])
v2=Vertex(2,[4,5])
v3=Vertex(3,[1,6])
v4=Vertex(4,[3,5,6,7])
v5=Vertex(5,[7])
v6=Vertex(6,[])
v7=Vertex(7,[6])
#创建一个长度为8的数组,来存储顶点,0索引元素不存
vlist = [False,v1,v2,v3,v4,v5,v6,v7]
def unweighted():
#起点为v3
vlist[3].dist = 0
q = Queue()
q.put(vlist[3])
while(not q.empty()):
v = q.get()#返回并删除队列头部元素
for w in v.outList:
if(vlist[w].dist == float('inf')):
vlist[w].dist = v.dist + 1
vlist[w].prev = v.vid
q.put(vlist[w])
unweighted()
print('v1.prev:',v1.prev,'v1.dist',v1.dist)
print('v2.prev:',v2.prev,'v2.dist',v2.dist)
print('v3.prev:',v3.prev,'v3.dist',v3.dist)
print('v4.prev:',v4.prev,'v4.dist',v4.dist)
print('v5.prev:',v5.prev,'v5.dist',v5.dist)
print('v6.prev:',v6.prev,'v6.dist',v6.dist)
print('v7.prev:',v7.prev,'v7.dist',v7.dist)
运行结果:
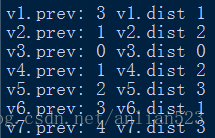
与数据变化表的最终情况一致。
这里你可能会问,Vertex类的init函数中,明明有know成员,为什么在程序没有使用know成员(在处理节点后,就把该节点的know置为Ture),因为if(vlist[w].dist == float('inf'))的判断就相当于判断节点的know是否为Ture,因为一个已知的节点,它的距离就肯定不是无穷大了。
然后再使用递归,打印出所有可能的最短路径,把以下代码和以上代码合在一起就可以了。
traj_list = [3]#v3是起点直接加上
def print_traj(dist):
last = traj_list[-1]
print(traj_list,'该路径的长度为:',vlist[last].dist)
temp_list = []#存储下一步的选项
for i in range(1,len(vlist)):
v = vlist[i]
if((v.dist==dist) and (v.prev==last)):
temp_list.append(i)
if(len(temp_list)==0):
return#终点
#递归每个选项
for i in temp_list:#i为顶点的索引
traj_list.append(i)
print_traj(dist+1)
traj_list.pop()
print_traj(1)

到此这篇关于python3实现无权最短路径的方法的文章就介绍到这了,更多相关python3 无权最短路径内容请搜索软件开发网以前的文章或继续浏览下面的相关文章希望大家以后多多支持软件开发网!