泛统计理论初探——余弦距离简介
介绍余弦距离
在衡量变量之间距离的时候,我们发现可以用欧式距离、绝对值距离,本文我们将来介绍另一种距离,即余弦距离。余弦距离在实际问题中经常用到,由于它的计算方法是把各个维度的点积相乘并相加,然后除以模长得到余弦相似度,再用1减去余弦相似度得到余弦距离,该方法和欧式距离等直接计算距离差的计算方法不同,可以较好地消除变量本身的数值大小带来的距离计算问题。
余弦相似度的公式如下: 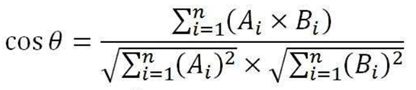
余弦距离=1-余弦相似度
根据上述的表达式,我们可以看到,余弦相似度就是把两个向量进行点积然后相加后去除以各自的模长,余弦相似度的实际含义如下图。
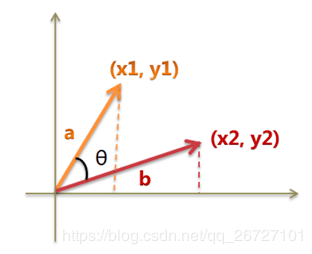
通过上图我们可以看出,余弦相似度是介于-1和1之间的值,如果上图的a向量和b向量的夹角是0度,那么余弦相似度是1,而余弦距离是0,即两者非常相似,没有差异。如果上图的a向量和b向量的夹角是90度,那么余弦相似度是0,余弦距离是1,即两者完全不相似,有很大的差异。
那么余弦距离和之前提到的欧式距离有哪些关系呢,下面我们来进行公式推导,首先是欧式距离的定义如下:
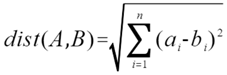
然后当A向量和B向量的模长进行归一化,让它们的模长都变为1,如下式子:
![]()
在这个时候,我们可以将欧式距离进行公式推导如下,发现欧式距离和余弦距离是可以通过推导得出的:
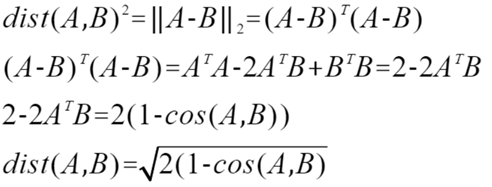
根据上述的公式推导,我们发现余弦距离公式和欧式距离公式在满足一定条件的时候可以互相转化,而余弦距离在应用时和欧式距离还是有差别的,余弦距离更关注两个变量之间的相对差异性,欧式距离更关注两个变量之间的绝对差异性。下面我们通过例子进行说明:
| 文章A-足球 | 文章B-篮球 | 文章C-育儿 | 文章D-综艺 | |
|---|---|---|---|---|
| 用户X | 1 | 1 | 0 | 0 |
| 用户Y | 0 | 0 | 1 | 1 |
有X用户和Y用户,平时看的文章的主题完全不同,X用户喜欢篮球类和足球类的文章,Y用户喜欢育儿类和综艺类的文章。所以它们之间的余弦距离和欧式距离分别是:(如果将上述数据进行归一化,是满足之前的公式推导的)
欧式距离=dist(X,Y)=2
余弦距离=1-cos(X,Y)=1
| 登录网站次数 | 平均观看时长 | |
|---|---|---|
| 用户U | 3 | 4 |
| 用户V | 30 | 40 |
有U用户和V用户,平时登录网站的次数和在网站上观看电影的时间长完全不同,U用户是不太登录这个网站的,而V用户则是这个电影网站的常驻用户。所以它们之间的余弦距离和欧式距离分别是:
欧式距离=dist(X,Y)=45
余弦距离=1-cos(X,Y)=0.93675
因此从上面两个案例我们发现,在第一个例子中,用户X和Y其实是完全不同的两类人,这个时候使用余弦距离衡量可以认为它们是完全没有共同点的,因为余弦距离值是1,达到了余弦距离的上限。在第二个例子中,用户U和V是完全不同的两类人,用户V比用户U要更活跃,通过欧式距离计算可以发现用户U和V是有很大差异的,但是余弦距离计算的效果不明显。即说明了在绝对差距问题上,使用欧式距离效果较好;在相对差距的问题上,使用余弦距离的效果更好。
值得注意的是,余弦距离不满足传统距离的三大公理,即正定性、对称性、三角不等式,所以使用者在使用余弦距离作为距离衡量标准需要慎重一些。
总的来说,余弦距离在衡量相对误差时是可以使用的,通常效果较好,但是由于其自身不满足欧氏空间的距离三大公理中的三角不等式性质,所以初学者使用时需要慎重一些。而欧式距离公式在绝对差异较为明显的问题上是可以使用的,也可以考虑绝对值距离公式,但对于一些离散型特征的问题,欧式距离公式的使用也需要慎重。
作者:喷火龙与水箭龟