python实现余弦相似度文本比较的示例
向量空间模型VSM:
VSM的介绍:
VSM的例子:
TF-IDF权重计算:
TF的由来:
IDF的出现:
TF-IDF的计算:
余弦相似度的计算:
文本比较实例:
对文本进行去停用词和分词:
余弦相似度代码实现:
向量空间模型VSM: VSM的介绍:一个文档可以由文档中的一系列关键词组成,而VSM则是用这些关键词的向量组成一篇文档,其中的每个分量代表词项在文档中的相对重要性。
VSM的例子:比如说,一个文档有分词和去停用词之后,有N个关键词(或许去重后就有M个关键词),文档关键词相应的表示为(d1,d2,d3,...,dn),而每个关键词都有一个对应的权重(w1,w1,...,wn)。对于一篇文档来说,或许所含的关键词项比较少,文档向量化后的向量维度可能不是很大。而对于多个文档(2篇文档或两篇文档以上),则需要合并所有文档的关键词(关键词不能重复),形成一个不重复的关键词集合,这个关键词集合的个数就是每个文档向量化后的向量的维度。打个比方说,总共有2篇文档A和B,其中A有5个不重复的关键词(a1,a2,a3,a4,a5),B有6个关键词(b1,b2,b3,b4,b5,b6),而且假设b1和a3重复,则可以形成一个简单的关键词集(a1,a2,a3,a4,a5,,b2,b3,b4,b5,b6),则A文档的向量可以表示为(ta1,ta2,ta3,ta4,ta5,0,0,0,0,0),B文档可以表示为(0,0,tb1,0,0,tb2,tb3,tb4,tb5,tb6),其中的tb表示的对应的词汇的权重。
最后,关键词的权重一般都是有TF-IDF来表示,这样的表示更加科学,更能反映出关键词在文档中的重要性,而如果仅仅是为数不大的文档进行比较并且关键词集也不是特别大,则可以采用词项的词频来表示其权重(这种表示方法其实不怎么科学)。
TF-IDF权重计算: TF的由来:以前在文档搜索的时候,我们只考虑词项在不在文档中,在就是1,不在就是0。其实这并不科学,因为那些出现了很多次的词项和只出现了一次的词项会处于等同的地位,就是大家都是1.按照常理来说,文档中词项出现的频率越高,那么就意味着这个词项在文档中的地位就越高,相应的权重就越大。而这个权重就是词项出现的次数,这样的权重计算结果被称为词频(term frequency),用TF来表示。
IDF的出现:在用TF来表示权重的时候,会出现一个严重的问题:就是所有 的词项都被认为是一样重要的。但在实际中,某些词项对文本相关性的计算来说毫无意义,举个例子,所有的文档都含有汽车这个词汇,那么这个词汇就没有区分能力。解决这个问题的直接办法就是让那些在文档集合中出现频率较高的词项获得一个比较低的权重,而那些文档出现频率较低的词项应该获得一个较高的权重。
为了获得出现词项T的所有的文档的数目,我们需要引进一个文档频率df。由于df一般都比较大,为了便于计算,需要把它映射成一个较小的范围。我们假设一个文档集里的所有的文档的数目是N,而词项的逆文档频率(IDF)。计算的表达式如下所示:
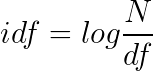
通过这个idf,我们就可以实现罕见词的idf比较高,高频词的idf比较低。
TF-IDF的计算:TF-IDF = TF * IDF
有了这个公式,我们就可以对文档向量化后的每个词给予一个权重,若不含这个词,则权重为0。
余弦相似度的计算:有了上面的基础知识,我们可以将每个分好词和去停用词的文档进行文档向量化,并计算出每一个词项的权重,而且每个文档的向量的维度都是一样的,我们比较两篇文档的相似性就可以通过计算这两个向量之间的cos夹角来得出。下面给出cos的计算公式:
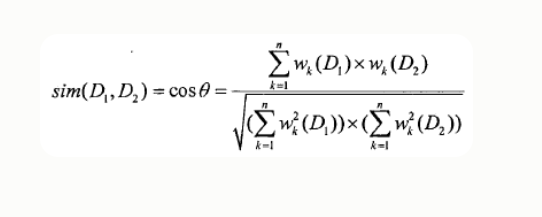
分母是每篇文档向量的模的乘积,分子是两个向量的乘积,cos值越趋向于1,则说明两篇文档越相似,反之越不相似。
文本比较实例: 对文本进行去停用词和分词:文本未分词前,如下图所示:
文本分词和去停用词后,如下图所示:

词频统计和文档向量化
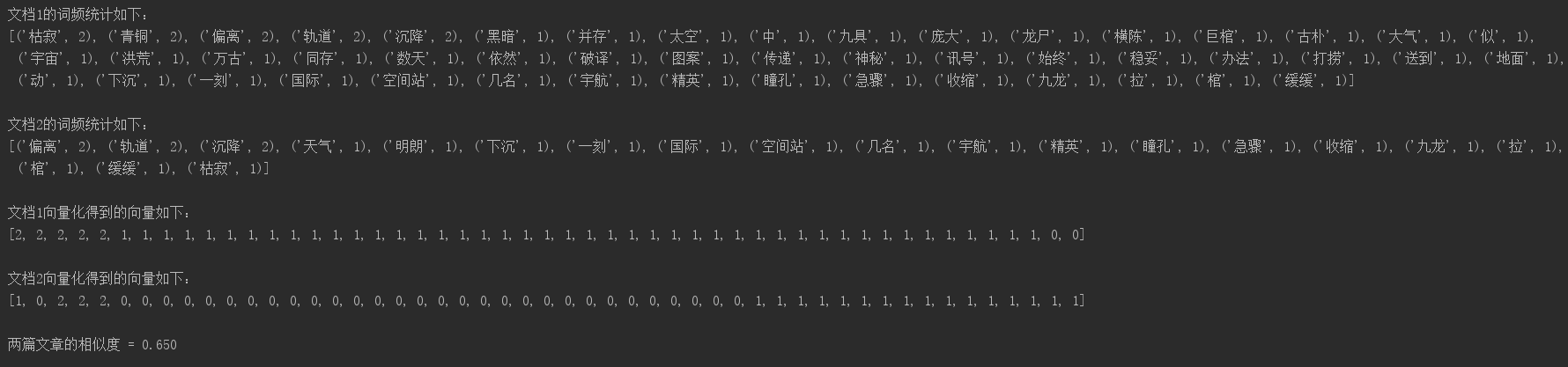
对经过上一步处理过的文档,我们可以统计每个文档中的词项的词频,并且将其向量化,下面我直接给出文档向量化之后的结果。注意:在这里由于只是比较两篇文档的相似性,所以我只用了tf来作为词项的权重,并未使用tf-idf:

向量化后的结果是:
[1,1,1,1,1,1,1,1,1,1,1,1,1,1]
两篇文档进行相似度的计算,我会给出两篇文档的原文和最终计算的相似度:
文档原文如下所示:

文档A的内容

文档B的内容
import math
# 两篇待比较的文档的路径
sourcefile = '1.txt'
s2 = '2.txt'
# 关键词统计和词频统计,以列表形式返回
def Count(resfile):
t = {}
infile = open(resfile, 'r', encoding='utf-8')
f = infile.readlines()
count = len(f)
# print(count)
infile.close()
s = open(resfile, 'r', encoding='utf-8')
i = 0
while i < count:
line = s.readline()
# 去换行符
line = line.rstrip('\n')
# print(line)
words = line.split(" ")
# print(words)
for word in words:
if word != "" and t.__contains__(word):
num = t[word]
t[word] = num + 1
elif word != "":
t[word] = 1
i = i + 1
# 字典按键值降序
dic = sorted(t.items(), key=lambda t: t[1], reverse=True)
# print(dic)
# print()
s.close()
return (dic)
def MergeWord(T1,T2):
MergeWord = []
duplicateWord = 0
for ch in range(len(T1)):
MergeWord.append(T1[ch][0])
for ch in range(len(T2)):
if T2[ch][0] in MergeWord:
duplicateWord = duplicateWord + 1
else:
MergeWord.append(T2[ch][0])
# print('重复次数 = ' + str(duplicateWord))
# 打印合并关键词
# print(MergeWord)
return MergeWord
# 得出文档向量
def CalVector(T1,MergeWord):
TF1 = [0] * len(MergeWord)
for ch in range(len(T1)):
TermFrequence = T1[ch][1]
word = T1[ch][0]
i = 0
while i < len(MergeWord):
if word == MergeWord[i]:
TF1[i] = TermFrequence
break
else:
i = i + 1
# print(TF1)
return TF1
def CalConDis(v1,v2,lengthVector):
# 计算出两个向量的乘积
B = 0
i = 0
while i < lengthVector:
B = v1[i] * v2[i] + B
i = i + 1
# print('乘积 = ' + str(B))
# 计算两个向量的模的乘积
A = 0
A1 = 0
A2 = 0
i = 0
while i < lengthVector:
A1 = A1 + v1[i] * v1[i]
i = i + 1
# print('A1 = ' + str(A1))
i = 0
while i < lengthVector:
A2 = A2 + v2[i] * v2[i]
i = i + 1
# print('A2 = ' + str(A2))
A = math.sqrt(A1) * math.sqrt(A2)
print('两篇文章的相似度 = ' + format(float(B) / A,".3f"))
T1 = Count(sourcefile)
print("文档1的词频统计如下:")
print(T1)
print()
T2 = Count(s2)
print("文档2的词频统计如下:")
print(T2)
print()
# 合并两篇文档的关键词
mergeword = MergeWord(T1,T2)
# print(mergeword)
# print(len(mergeword))
# 得出文档向量
v1 = CalVector(T1,mergeword)
print("文档1向量化得到的向量如下:")
print(v1)
print()
v2 = CalVector(T2,mergeword)
print("文档2向量化得到的向量如下:")
print(v2)
print()
# 计算余弦距离
CalConDis(v1,v2,len(v1))
到此这篇关于python实现余弦相似度文本比较的文章就介绍到这了,更多相关python余弦相似度内容请搜索软件开发网以前的文章或继续浏览下面的相关文章希望大家以后多多支持软件开发网!