牛客练习赛62(基于官方题解的补题 A ~ D)
难度中等,需要一定的分析,主要是跟榜跟的心态爆炸了,感觉A C D 比B好想一些
A-牛妹的游戏题意:给你n节点m条边的无向图,问原图和补图是否有三元环。
做法:知道不合法的肯定很少,但不知道怎么暴力求三元环(这里的确是菜了,其实很简单,就枚举三个点i-j j-k k-i 就可以了)

#include
#define rep(i,a,b) for(int i=a;i=(b);--i)
#define mem(a,x) memset(a,x,sizeof(a))
#define pb push_back
#define pi pair
#define mk make_pair
using namespace std;
typedef long long ll;
ll gcd(ll a,ll b) { return b?gcd(b,a%b):a;}
const int N=100;
int n,m,flag;
int dp[N][N];
void solve()
{
scanf("%d%d",&n,&m);
if(n>18){
int u,v;
rep(i,1,m) scanf("%d%d",&u,&v);
puts("yes");
return ;
}
mem(dp,0);
rep(i,1,m){
int u,v;
scanf("%d%d",&u,&v);
dp[u][v]=dp[v][u]=1;
}
flag=0;
for(int i=1;i<=n;++i){
for(int j=i+1;j<=n;++j){
for(int k=j+1;k>_;while(_--)
solve();
}
B-病毒扩散


直接按照题意来很难写,需要转换:

能想到这个题意模型有点不容易。
#include
#define rep(i,a,b) for(int i=a;i=(b);--i)
#define mem(a,x) memset(a,x,sizeof(a))
#define pb push_back
#define pi pair
#define mk make_pair
using namespace std;
typedef long long ll;
ll gcd(ll a,ll b) { return b?gcd(b,a%b):a;}
const int N=5e3+10;
const ll mod=998244353 ;
ll f[N];
void init()
{
f[0]=1;
rep(i,1,N-1) f[i]=f[i-1]*i%mod;
}
ll powmod(ll a,ll b)
{
ll res=1;
for(;b;b>>=1){
if(b&1) res=res*a%mod;
a=a*a%mod;
}
return res;
}
ll C(int n,int m)
{
return f[n]*powmod(f[m],mod-2)%mod*powmod(f[n-m],mod-2)%mod;
}
void solve()
{
int x,y,t;
scanf("%d%d%d",&x,&y,&t);
if(t>_;while(_--)
solve();
}
C-牛牛染颜色

做法,经典树形dp:dp[u][0]代表u这个节点不为黑色的方案数,dp[u][1]代表u这个节点变为黑色节点的个数
dp[u][1]的方案数好计算,dp[u][1]=
#include
#define rep(i,a,b) for(int i=a;i=(b);--i)
#define mem(a,x) memset(a,x,sizeof(a))
#define pb push_back
#define pi pair
#define mk make_pair
using namespace std;
typedef long long ll;
ll gcd(ll a,ll b) { return b?gcd(b,a%b):a;}
const ll mod=1e9+7;
const int N=1e6+10;
struct node
{
int v,ne;
}e[2*N];
int head[N],cnt;
int n;
ll dp[N][2];
void add(int u,int v)
{
e[++cnt]={v,head[u]};
head[u]=cnt;
e[++cnt]={u,head[v]};
head[v]=cnt;
}
void dfs(int u,int fa)
{
dp[u][0]=1;
dp[u][1]=1;
for(int i=head[u];i;i=e[i].ne){
int v=e[i].v;
if(v==fa) continue;
dfs(v,u);
dp[u][1]=dp[u][1]*(dp[v][0]+dp[v][1])%mod;
dp[u][0]=(dp[u][0]+dp[v][1]+dp[v][0]-1)%mod;
}
}
void solve()
{
scanf("%d",&n);
rep(i,2,n)
{
int u,v;
scanf("%d%d",&u,&v);
add(u,v);
}
dfs(1,-1);
printf("%lld\n",(dp[1][1]+dp[1][0])%mod);
}
int main()
{
//int _;cin>>_;while(_--)
solve();
}
D-牛牛的呱数
题意:

没看到数据范围,没想到p这么的小
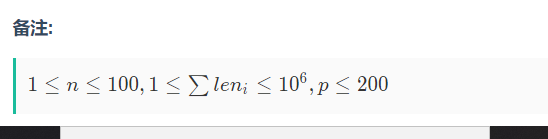
其实就是特别简单的bfs一下,将所有的模数全部覆盖即可。每次bfs取出当前数now 那就从n个里面进行连接即可。。
#include
using namespace std;
const int N=2e2+10,M=1e6+10;
typedef long long ll;
ll dp[N],a[N],mod,f[M];
int vis[N],len[N],n;
int main()
{
cin>>n>>mod;
f[0]=1;
for(int i=1;i<M;++i) f[i]=f[i-1]*10%mod;
for(int i=0;i<N;++i) dp[i]=1e18+10;
for(int i=1;i>s;
int now=0;
for(int j=0;j<s.size();++j)now=(now*10+s[j]-'0')%mod;
a[i]=now;
len[i]=s.size();
dp[now]=min(dp[now],1ll*len[i]);
}
queueque;
for(int i=0;i<mod;++i) if(dp[i]<1e18) que.push(i),vis[i]=1;
while(que.size()){
int now=que.front();que.pop();
vis[now]=0;
for(int i=1;idp[now]+len[i]){
dp[ne]=dp[now]+len[i];
if(vis[now]==0){
vis[ne]=1;
que.push(ne);
}
}
}
}
if(dp[0]==1e18+10)dp[0]=-1;
printf("%lld\n",dp[0]);
}
作者:ccsu_deer