如何使用R语言做逻辑回归详解
前言
首先加载需要用的包
接下来建模
最后我们可以根据模型来预测啦
总结
前言回归的本质是建立一个模型用来预测,而逻辑回归的独特性在于,预测的结果是只能有两种,true or false
在R里面做逻辑回归也很简单,只需要构造好数据集,然后用glm函数(广义线性模型(generalized linear model))建模即可,预测用predict函数。
我这里简单讲一个例子,来自于加州大学洛杉矶分校的课程
首先加载需要用的包library(ggplot2)
## Warning: package 'ggplot2' was built under R version 3.1.3
library(Rcpp)
## Warning: package 'Rcpp' was built under R version 3.2.2
然后加载测试数据
mydata <- read.csv("http://www.ats.ucla.edu/stat/data/binary.csv")
## 这里直接读取网络数据
head(mydata)
## admit gre gpa rank
## 1 0 380 3.61 3
## 2 1 660 3.67 3
## 3 1 800 4.00 1
## 4 1 640 3.19 4
## 5 0 520 2.93 4
## 6 1 760 3.00 2
#This dataset has a binary response (outcome, dependent) variable called admit.
#There are three predictor variables: gre, gpa and rank. We will treat the variables gre and gpa as continuous.
#The variable rank takes on the values 1 through 4.
summary(mydata)
## admit gre gpa rank
## Min. :0.0000 Min. :220.0 Min. :2.260 Min. :1.000
## 1st Qu.:0.0000 1st Qu.:520.0 1st Qu.:3.130 1st Qu.:2.000
## Median :0.0000 Median :580.0 Median :3.395 Median :2.000
## Mean :0.3175 Mean :587.7 Mean :3.390 Mean :2.485
## 3rd Qu.:1.0000 3rd Qu.:660.0 3rd Qu.:3.670 3rd Qu.:3.000
## Max. :1.0000 Max. :800.0 Max. :4.000 Max. :4.000
sapply(mydata, sd)
## admit gre gpa rank
## 0.4660867 115.5165364 0.3805668 0.9444602
xtabs(~ admit + rank, data = mydata) ##保证结果变量只能是录取与否,不能有其它!!!
## rank
## admit 1 2 3 4
## 0 28 97 93 55
## 1 33 54 28 12
可以看到这个数据集是关于申请学校是否被录取的,根据学生的GRE成绩,GPA和排名来预测该学生是否被录取。
其中GRE成绩是连续性的变量,学生可以考取任意正常分数。
而GPA也是连续性的变量,任意正常GPA均可。
最后的排名虽然也是连续性变量,但是一般前几名才有资格申请,所以这里把它当做因子,只考虑前四名!
而我们想做这个逻辑回归分析的目的也很简单,就是想根据学生的成绩排名,绩点信息,托福或者GRE成绩来预测它被录取的概率是多少!
接下来建模mydata$rank <- factor(mydata$rank)
mylogit <- glm(admit ~ gre + gpa + rank, data = mydata, family = "binomial")
summary(mylogit)
##
## Call:
## glm(formula = admit ~ gre + gpa + rank, family = "binomial",
## data = mydata)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.6268 -0.8662 -0.6388 1.1490 2.0790
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -3.989979 1.139951 -3.500 0.000465 ***
## gre 0.002264 0.001094 2.070 0.038465 *
## gpa 0.804038 0.331819 2.423 0.015388 *
## rank2 -0.675443 0.316490 -2.134 0.032829 *
## rank3 -1.340204 0.345306 -3.881 0.000104 ***
## rank4 -1.551464 0.417832 -3.713 0.000205 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 499.98 on 399 degrees of freedom
## Residual deviance: 458.52 on 394 degrees of freedom
## AIC: 470.52
##
## Number of Fisher Scoring iterations: 4
根据对这个模型的summary结果可知:
GRE成绩每增加1分,被录取的优势对数(log odds)增加0.002
而GPA每增加1单位,被录取的优势对数(log odds)增加0.804,不过一般GPA相差都是零点几。
最后第二名的同学比第一名同学在其它同等条件下被录取的优势对数(log odds)小了0.675,看来排名非常重要啊!!!
这里必须解释一下这个优势对数(log odds)是什么意思了,如果预测这个学生被录取的概率是p,那么优势对数(log odds)就是log2(p/(1-p)),一般是以自然对数为底
最后我们可以根据模型来预测啦## 重点是predict函数,type参数
newdata1 <- with(mydata,
data.frame(gre = mean(gre), gpa = mean(gpa), rank = factor(1:4)))
newdata1
## gre gpa rank
## 1 587.7 3.3899 1
## 2 587.7 3.3899 2
## 3 587.7 3.3899 3
## 4 587.7 3.3899 4
## 这里构造一个需要预测的矩阵,4个学生,除了排名不一样,GRE和GPA都一样
newdata1$rankP <- predict(mylogit, newdata = newdata1, type = "response")
newdata1
## gre gpa rank rankP
## 1 587.7 3.3899 1 0.5166016
## 2 587.7 3.3899 2 0.3522846
## 3 587.7 3.3899 3 0.2186120
## 4 587.7 3.3899 4 0.1846684
## type = "response" 直接返回预测的概率值0~1之间
可以看到,排名越高,被录取的概率越大!!!
log(0.5166016/(1-0.5166016)) ## 第一名的优势对数0.06643082
log((0.3522846/(1-0.3522846))) ##第二名的优势对数-0.609012
两者的差值正好是0.675,就是模型里面预测的!
newdata2 <- with(mydata,
data.frame(gre = rep(seq(from = 200, to = 800, length.out = 100), 4),
gpa = mean(gpa), rank = factor(rep(1:4, each = 100))))
##newdata2
##这个数据集也是构造出来,需要用模型来预测的!
newdata3 <- cbind(newdata2, predict(mylogit, newdata = newdata2, type="link", se=TRUE))
## type="link" 返回fit值,需要进一步用plogis处理成概率值
## ?plogis The Logistic Distribution
newdata3 <- within(newdata3, {
PredictedProb <- plogis(fit)
LL <- plogis(fit - (1.96 * se.fit))
UL <- plogis(fit + (1.96 * se.fit))
})
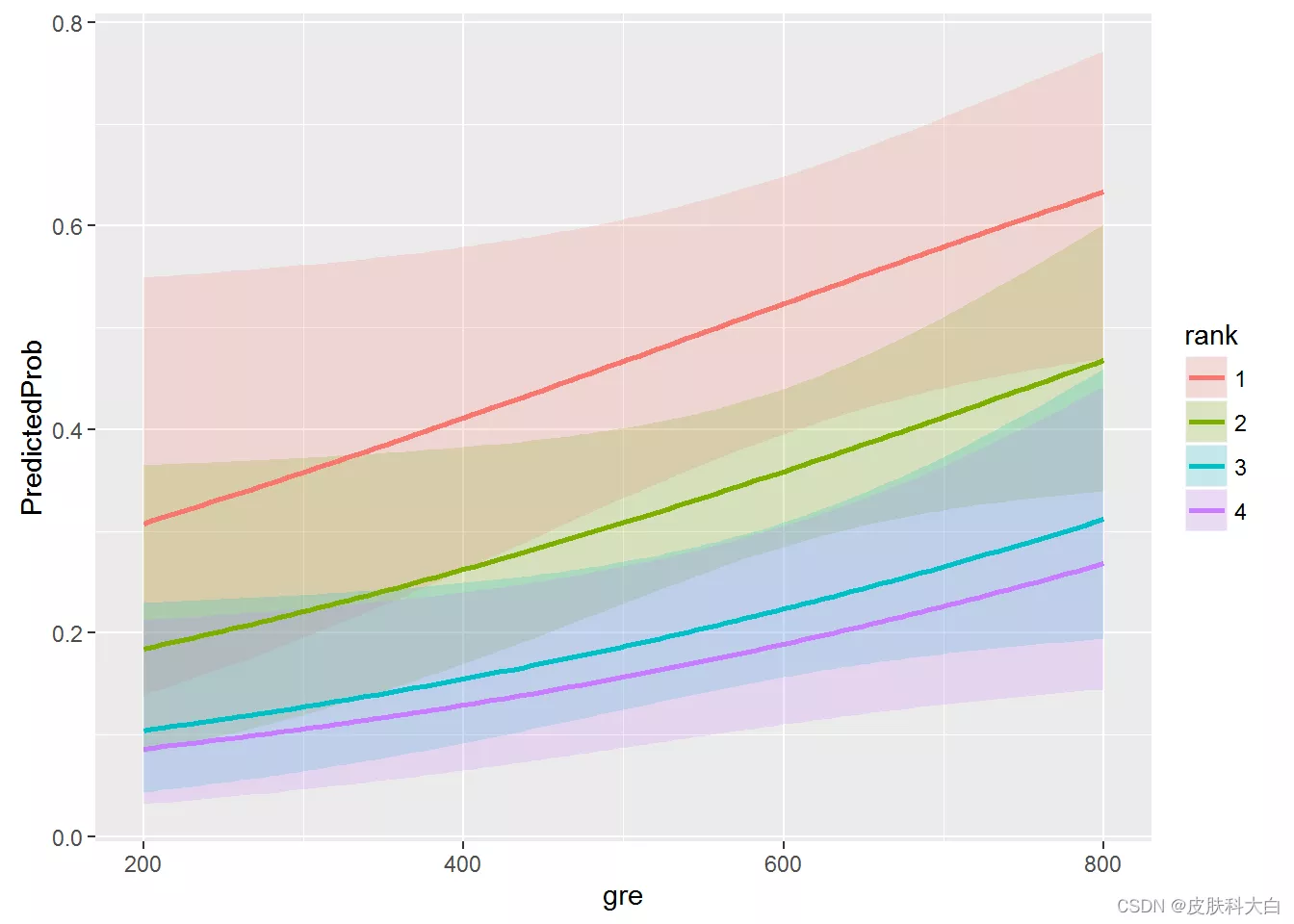
最后可以做一些简单的可视化
head(newdata3)
## gre gpa rank fit se.fit residual.scale UL
## 1 200.0000 3.3899 1 -0.8114870 0.5147714 1 0.5492064
## 2 206.0606 3.3899 1 -0.7977632 0.5090986 1 0.5498513
## 3 212.1212 3.3899 1 -0.7840394 0.5034491 1 0.5505074
## 4 218.1818 3.3899 1 -0.7703156 0.4978239 1 0.5511750
## 5 224.2424 3.3899 1 -0.7565919 0.4922237 1 0.5518545
## 6 230.3030 3.3899 1 -0.7428681 0.4866494 1 0.5525464
## LL PredictedProb
## 1 0.1393812 0.3075737
## 2 0.1423880 0.3105042
## 3 0.1454429 0.3134499
## 4 0.1485460 0.3164108
## 5 0.1516973 0.3193867
## 6 0.1548966 0.3223773
ggplot(newdata3, aes(x = gre, y = PredictedProb)) +
geom_ribbon(aes(ymin = LL, ymax = UL, fill = rank), alpha = .2) +
geom_line(aes(colour = rank), size=1)
到此这篇关于如何使用R语言做逻辑回归的文章就介绍到这了,更多相关R语言逻辑回归内容请搜索软件开发网以前的文章或继续浏览下面的相关文章希望大家以后多多支持软件开发网!