手把手带你熟悉Dijkstra算法
伪代码
STEP2
STEP3
STEP4
STEP5
结果
编程实现
作者:进阶的JFarmer
//u是源节点
Initialization:
N' = {u}
for all nodes v
if v is a neighbor of u
then D(v) = c(u,v)
e1se D(v) =∞
Loop
find w not in N' such that D(w) is a minimum
add w to N'
update D(v) for each neighbor v of w and not in N':
D(v) = min(D(v) , D(w) + c(w,v))
//new cost to v is either old cost to v or known 1east path cost to w plus cost from w to v
until N'= N
例题
如下图,源点选为u。
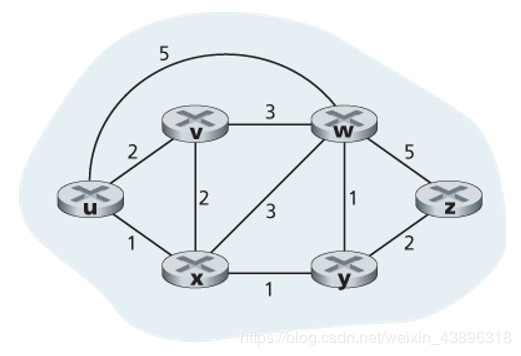
已并入结点:{u}
初始化列表:
| 结点 | 最短距离 | 路径 |
|---|---|---|
| v | 2 | {u, v} |
| w | 5 | {u, w} |
| x | 1 | {u, x} |
| y | ∞ | null |
| z | ∞ | null |
接下来,找距离u最近的一个结点,那就是x了!
已并入结点:{u, x}
| 结点 | 最短距离 | 路径 |
|---|---|---|
| x | 1 | {u, x} |
| v | 2 | min(d(u, v), d(u, x)+d(x, v)) = min(2, 3) => {u, v} |
| w | 4 | min(d(u, w), d(u, x)+d(x, w)) = min(5, 4) => {u, x, w} |
| y | 2 | {u, x, y} |
| z | ∞ | null |
接下来,找距离u最近的一个结点,那就是v了!
已并入结点:{u, x, v}
| 结点 | 最短距离 | 路径 |
|---|---|---|
| x | 1 | {u, x} |
| v | 2 | {u, v} |
| w | 4 | min(d(u, x, w), d(u, v)+d(v, w)) = min(4, 5) => {u, x, w} |
| y | 2 | {u, x, y} |
| z | ∞ | null |
接下来,找距离u最近的一个结点,那就是y了!
已并入结点:{u, x, v, y}
| 结点 | 最短距离 | 路径 |
|---|---|---|
| x | 1 | {u, x} |
| v | 2 | {u, v} |
| y | 2 | {u, x, y} |
| w | 3 | min(d(u, x, w), d(u, x, y)+d(y, w)) = min(4, 3) => {u, x, y, w} |
| z | 4 | {u, x, y, z} |
接下来,找距离u最近的一个结点,那就是w了!
已并入结点:{u, x, v, y, w}
| 结点 | 最短距离 | 路径 |
|---|---|---|
| x | 1 | {u, x} |
| v | 2 | {u, v} |
| y | 2 | {u, x, y} |
| w | 3 | {u, x, y, w} |
| z | 4 | min(d(u, x, y, z), d(u, x, y, w)+d(w, z)) = min(4, 8) => {u, x, y, z} |
以u为单源节点,到达其他各个结点的最短路径及其代价是:
| 结点 | 最短距离 | 路径 |
|---|---|---|
| v | 2 | {u, v} |
| w | 3 | {u, x, y, w} |
| x | 1 | {u, x} |
| y | 2 | {u, x, y} |
| z | 4 | {u, x, y, z} |
《实现图论的Dijkstra算法和Prim算法(Python语言描述)》
实践性实验《Dijkstra算法解决欧洲旅行问题(Java语言描述)》
作者:进阶的JFarmer