机器智能-高频问题:博弈
1、博弈:竞争环境中多个agent之间的目标是有冲突的,称为对抗搜索问题,也称为博弈。
2、特点:问题复杂,注重时间效率(时间要求高),实时性强;
3、博弈一般都是有完整信息的,确定的,轮流行动的,两个游戏者的零和游戏(利弊等值,结果加起来等于0)
4、零和游戏:在严格竞争下,一方的收益必然意味着另一方的损失,博弈各方的收益和损失相加总和永远为“零”,双方不存在合作的可能
5、博弈游戏,目的是寻找最优的方案使得自己能够利益最大化
6、效用值:表示状态好坏,效用值越大对max选手有利;越小对min选手有利
7、极小极大算法:
a、博弈树的最优策略通过检查每个节点的极大极小值来决定。max走有极大值的节点,min走极小值的节点
b、从一开始,就已经得到了所有的可能的下棋方式和可能的结果并记录了所有的方式的效用值,在分出胜负之后才进行回溯。
c、举例:注意注意注意!!!
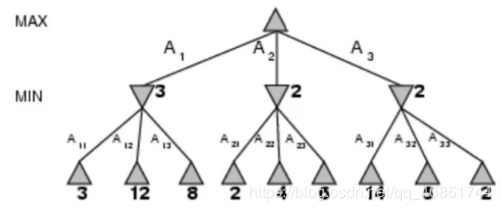
以上图为例,上图中的叶子节点是遍历一遍树到底的时候得到的结果,而中间节点的值是通过回溯的时候得到的。
| 叶子节点 | 产生影响 |
|---|---|
| A11-3 | 这个时候min会让max走这条支路最大能拿到3(当前情况),所以中间节点A1为<=3 |
| A12-12 | 这个时候会进行判断12与3的大小,因为如果走了这条支路,min不可能让max拿到12,所以对于A1节点不影响,仍旧为<=3 |
| A13-8 | 这个时候判断8与3的大小,还是比3大,所以min也不可能让max拿到,也就是说,如果max选择了支路A1,那么min必定会选择支路A11,所以中间节点A1的值为3(此时支路A1的子节点已经遍历完全,所以值可以确定) |
A2支路和A3支路同理,所以得到上面的图,也就是说,如果max走了A1支路,那么min能够让他拿到的最大值是3,如果走了A2支路,那么min能够让他拿到的最大值是2,A3同理
从上图可以看出,B总是选择候选方案中的最小值,而A总是选择候选方案中的最大值,极小极大的名字也就源于此。该算法使用深度优先搜索遍历决策树来填充树中间节点的利益值,叶子节点的利益值通常是通过一个利益评估函数算。
注意,在不是自己的选择中填充的数字(即上图中的圆将会填充的数字)是选择了该条分支后对手做出反应后我能得到的实际的结果。
d、时间复杂度:bn,空间复杂度:bn,和深度优先类似。
e、搜索深度有限时是完备的,深度无限不完备
f、极大极小值是一个最优算法,因为遍历了所有的可能。
g、是一个嵌套递归(有一个max选手函数和一个min选手函数,直到游戏结束才终止递归)
8、多人博弈:存在一个联盟与破坏联盟的问题,所以不能简单地考虑让自己的值最大。用向量值取代单一值,通常选择使自己效用值最大的行为。
9、α-β剪枝:通过剪枝消除对部分状态的搜索
a、从一开始,就已经得到了所有的可能的下棋方式和可能的结果并记录了所有的方式的效用值,在分出胜负之后才进行回溯。
b、游戏状态数目的增长是指数级的
c、是否剪枝与分支排列顺序有关
d、if(u>b)then return u;a<–max(a,u)发生剪枝的部分
e、相当于极小极大法的升级
f、假设α为下界,β为上界,对于α ≤ N ≤ β: 若 α ≤ β 则N有解;若 α > β 则N无解。
g、还是以下图为例:注意注意注意!!!

以上图为例,上图中的叶子节点是遍历一遍树到底的时候得到的结果,而中间节点的值是通过回溯的时候得到的,只不过他在回溯的过程中会进行判断,这条支路有没有可能性,从而发生剪枝来减少这棵树。
| 叶子节点 | 产生影响 |
|---|---|
| A11-3 | 这个时候min会让max走这条支路最大能拿到3(当前情况),所以中间节点A1为<=3 |
| A12-12 | 这个时候会进行判断12与3的大小,因为如果走了这条支路,min不可能让max拿到12,所以对于A1节点不影响,仍旧为<=3 |
| A13-8 | 这个时候判断8与3的大小,还是比3大,所以min也不可能让max拿到,也就是说,如果max选择了支路A1,那么min必定会选择支路A11,所以中间节点A1的值为3(此时支路A1的子节点已经遍历完全,所以值可以确定) |
| A21-2 | 这个时候min会让max走支路A2所能得到的最大值为2,而由于第一条支路的值已经为3大于2,所以max绝对不会走A2支路,那么A2支路剩余的子节点就不需要在进行考虑了 |
| A31-14 | 这个时候得到的值为14,即目前如果max走A3支路,min可能让max拿到的值<=14,继续探索 |
| A31-5 | 14比5小,所以min能让max拿到的值<=5 |
| A31-2 | 2比5小,所以min能让max拿到的值<=2 |
h、时空复杂度理论上与极小极大相同,可能在过程上有剪枝会有一点减小
i、执行结果是最优的
j、资源限制(阶段回溯):当遇到大的问题时搜索空间非常大,解决方法如下:
①、评估函数:在中间节点的执行结果与真实情况相同。反映出的优势大小应该与取胜的概率成正比。计算时间不能太长。如国际象棋(特征加权法):未考虑时间因素对棋子数量差产生的局势差异的影响以及棋子位置。
②、截断测试:限制搜索深度或搜索时间;效用值替换为评估值
作者:HNU君陌