2020编译原理练习记录------40分大题揭幕(3)
经过两周的学习,我们知道了如何用NFA转化为DFA,今天带来的是一道比较综合的大题,涵盖了学过的正规文法,NFA,DFA…
作者:每天精彩多一点
题目是这样描述的:有一个正规文法G[S]:S→aA|bQ, A→aA|bB|b, B→bD|aQ, Q→aQ|bD|b, D→bB|aA, E→aB|bF, F→bD|aE|b, 求此文法构造的最小化DFA。
这里的新颖的地方就是怎么把正规文法转化为NFA,下面就分步骤回顾一下(^_−)☆
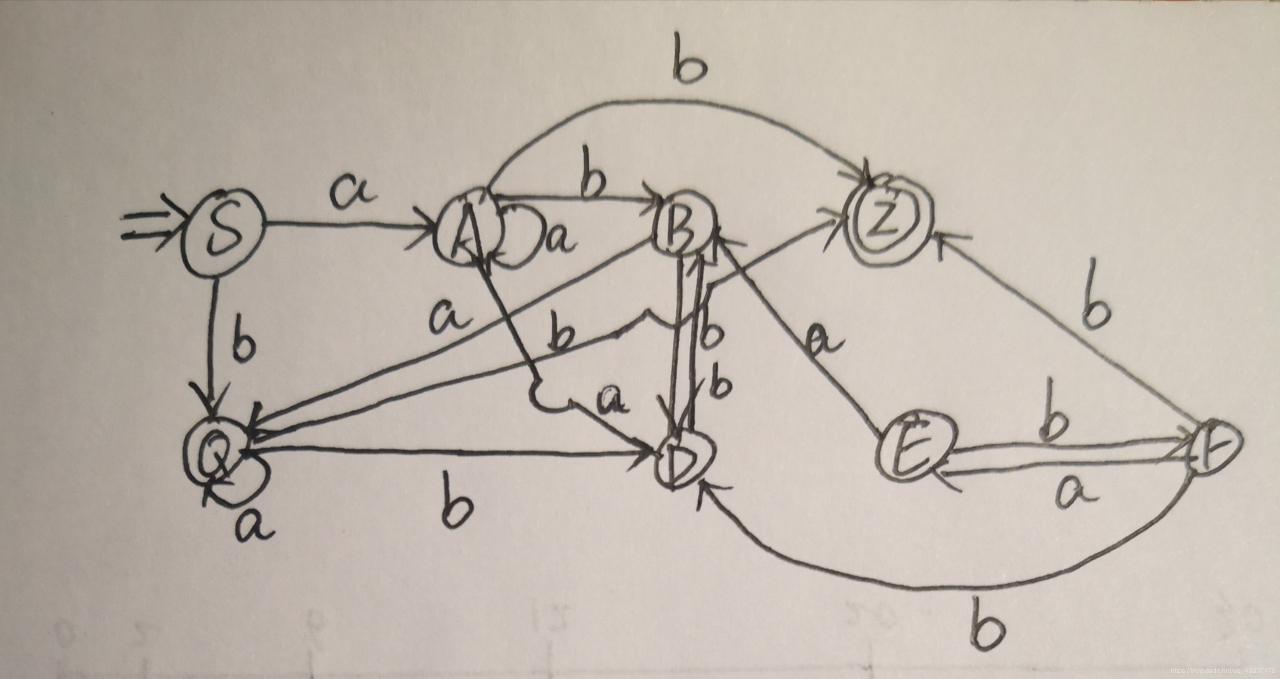
1.将正规文法转化为NFA
根据第一个S→aA|bQ,我们得出的是S可以作为一个起始符,S经过a到达A,S经过b到达Q,下面的例子都是相同的,我们只需要将完整的图画出来,这里可能有的人还有疑问,比方说Q→b这个怎么画呀?所以这里我们的处理方法就是Q经过b到达一个自己构造的终态Z。剩下的就轻而易举的,画好的图如下所示,这就是第一步NFA:
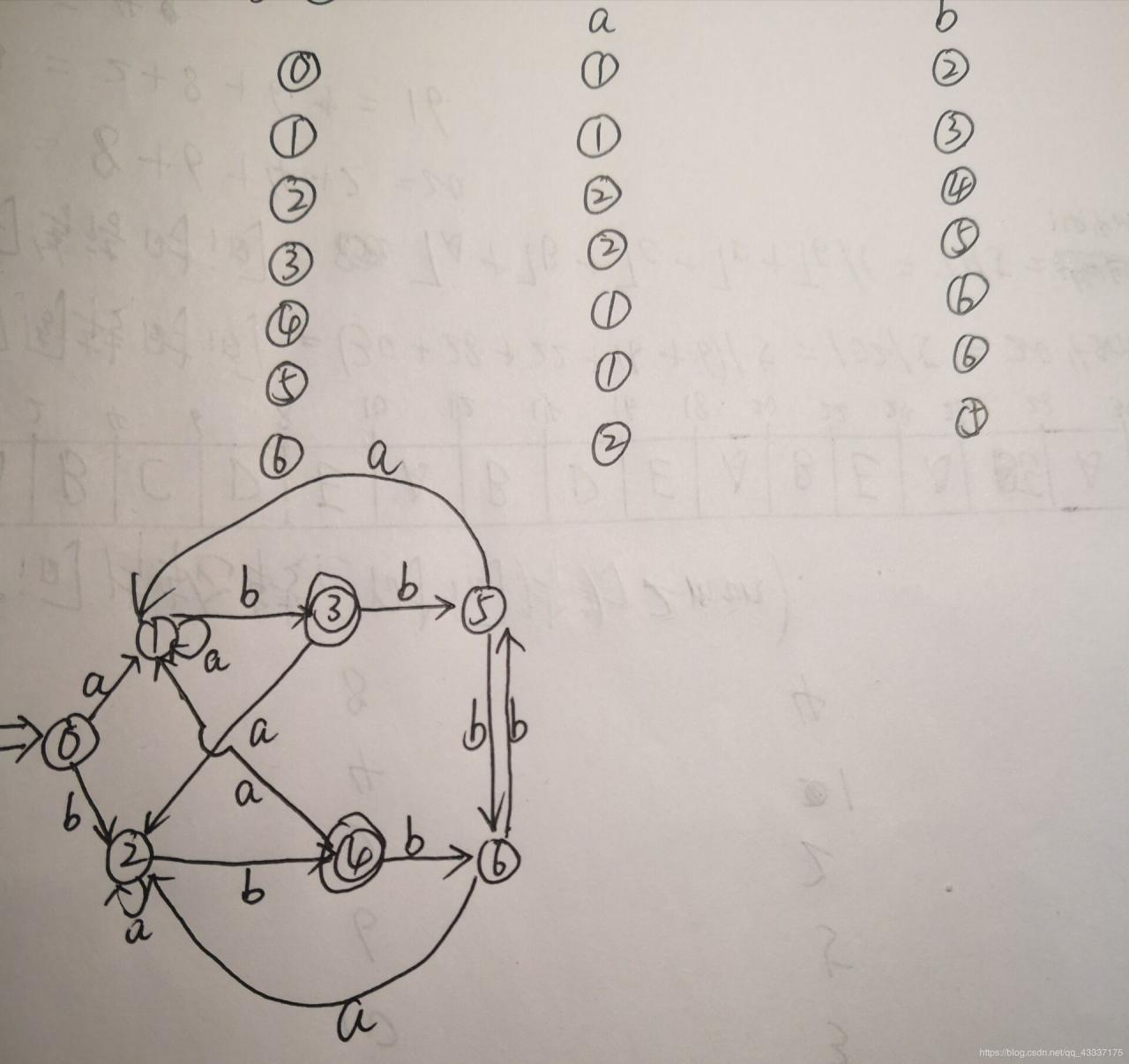
2.用子集法将NFA转化为DFA
由初始态S开始走,每次经过的再进行比较,如果左面没有就写到左面继续比较。
然后用新标的号码将这些关系连接起来就是我们所求的DFA了:
3.最后一步,也就是将求得的DFA最小化:
首先将终态和非终态分开:
然后看他们经过a,b都经过什么再进行进一步判断,直到不能再分。
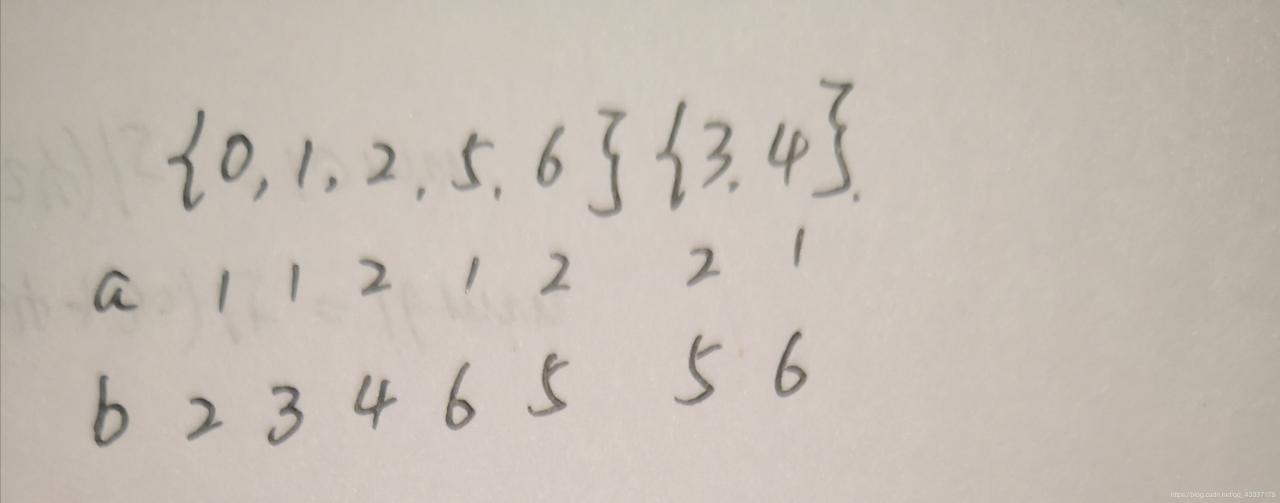
第一步可以看出1和2经过b到达了终态,所以将1和2分出来:

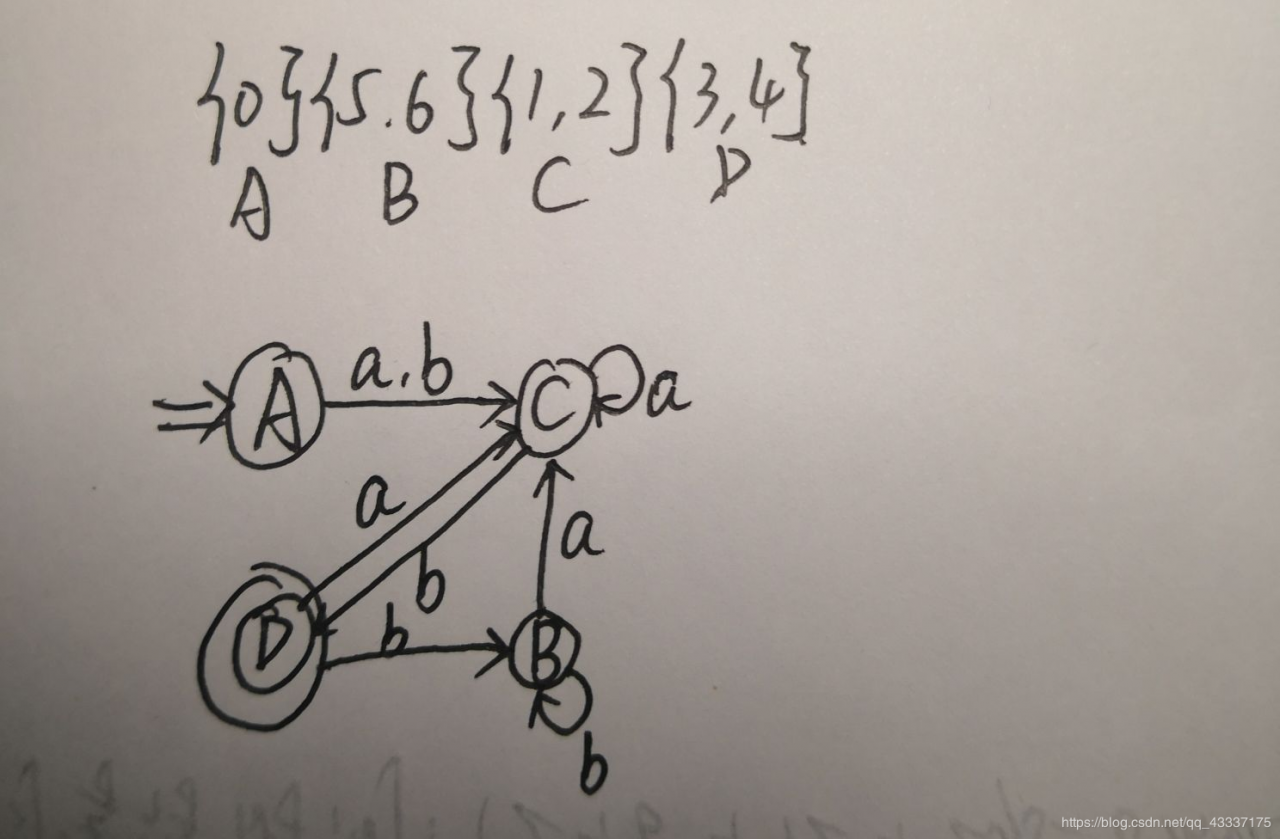
作者:每天精彩多一点