多元回归-最小二乘法-残差分析

我们需要进行以下六个假设，这些假设是经典的多元线性回归模型有效的前提：

1、因变量Y和自变量X1，X2，…，Xk之间的关系是线性的。

2、自变量（X1，X2，…，Xk）不是随机的。而且，两个或多个自变量之间不存在精确的线性关系。

3、以自变量为条件的残差的期望值为0：E（ε|X1，X2，…，Xk）=0。

4、残差项的方差对于所有观察值都是相同的：E（εi2）=σε2。

5、残差项在各个观测值之间是不相关的：E（εiεj）=0，j≠i。

6、残差项是正态分布的。

1、解释变量是确定变量，不是随机变量。
2、随机误差项具有零均值、同方差何不序列相关性。
3、随机误差项与解释变量之间不相关。
4、随机误差项服从零均值、同方差、零协方差的正态分布。

在回归模型中，假定残差的期望值为0，方差相等且服从正态分布的一个随机变量。但是，若关于残差的假定不成立，此时所做的检验以及估计和预测也许站不住脚。确定有关残差的假定是否成立的方法之一是进行残差分析（residual analysis）.

回归模型下的预测值和观测值之间的差异必须是随机不可预测的。
换句话说，在误差(error)中不应该含有任何可解释、可预测的信息。

①残差是否服从均值为零的正态分布；

②残差是否为等方差的正态分布；

③残差序列是否独立；

④借助残差探测样本中的异常值。

看分布-绘制残差图
看独立-DW检验

1-1残差图的定义：是指以某种残差为纵坐标，以其他适宜的量为横坐标的散点图。
这里横坐标有多种选择，最常见的选择是：
1.因变量的拟合值；
2. 某自变量的观察值；
3.在因变量的观察值Y1，…，Yn为一时间序列时， 横坐标可取为观察时间或观察序号。

1-2最常见的残差图——回归值与残差的残差图

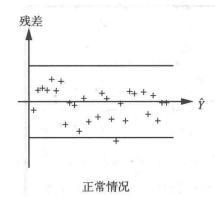
不论回归值的大小，而残差(或)具有相同的分布，并满足模型的各假设条件；

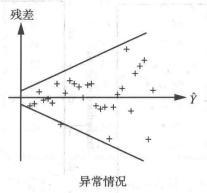
表示回归值的大小与残差的波动大小有关系，即等方差性的假设有问题；

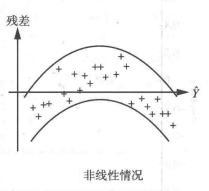
表示线性模型不合适的样本，可能有异常值存在。

参考链接：
https://baike.sogou.com/v7666692.htm?fromTitle=%E6%AE%8B%E5%B7%AE%E5%9B%BE

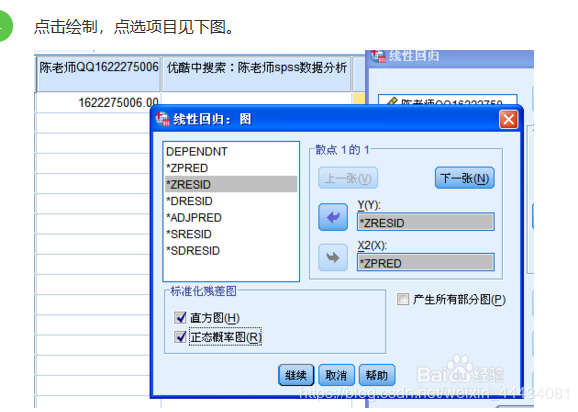
1-3在“绘制”那个窗口中的含义：

“DEPENDNT”：因变量
“ZPRED”：标准化预测值
“ZRESID”：标准化残差
“DRESID”：删除残差
“ADJPRED”：调节预测值
“SRESID”：学生化残差
“SDRESID”：学生化删除残差

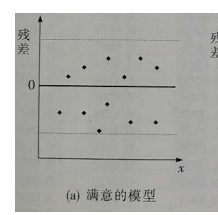
–检定回归模型中残差独立的假设
–如果相邻残差项间是相关，则其总差异必小或大
•若残差项间是正相关，则其差异必小
•若残差项间是负相关，则其差异必大
–当DW值愈接近2时，残差项间愈无相关
–当DW值愈接近0时，残差项间正相关愈强
–当DW值愈接近4时，残差项间负相关愈强

参考链接：https://jingyan.baidu.com/article/cbcede0715078502f40b4d05.html

多元回归 残差分析 残差 最小二乘法 回归