（三）【矩阵论】（子空间）常见子空间|基扩张定理|和空间与交空间|直和

Gaia ·

更新时间:2024-11-11

· 556 次阅读

【矩阵论专栏】

文章目录A 子空间定义B 常见的子空间C 基扩张定理D 和空间与交空间E 直和 A 子空间定义

定义1（子空间）：设VVV是数域FFF上的线性空间，WWW是VVV的子集，若对WWW中的任意元素α\alphaα,β\betaβ,及数k∈Fk\in Fk∈F,按VVV中的加法和数乘有：1)α+β∈W1)\alpha+\beta\in W1)α+β∈W2)kα∈W2)k\alpha\in W2)kα∈W则WWW也是数域FFF上的线性空间，称WWW为VVV的线性子空间，简称子空间

注：

由单个零元素组成的子集{0}\{0\}{0}是线性子空间；线性空间VVV是线性子空间。
000与VVV是称为VVV的平凡子空间。 dim{0}=1 B 常见的子空间

设AAA是一给定的m∗nm * nm∗n实矩阵，记N(A)≜{x∈Rn∣Ax=0}N(A)\triangleq\{x\in \mathbb{R}^n| Ax=0\} N(A)≜{x∈Rn∣Ax=0}R(A)≜{Ax∣x∈Rn}R(A) \triangleq\{Ax|x\in\mathbb{R}^n\}R(A)≜{Ax∣x∈Rn}则称N(A)N(A)N(A)是Rn\mathbb{R}^nRn的子空间，称为AAA的零空间。
则R(A)R(A)R(A)是Rn\mathbb{R}^nRn的子空间，称为A的列空间。dimN(A)=n−rankA=n−rdimN(A)=n-rankA=n-rdimN(A)=n−rankA=n−rAx=0Ax=0Ax=0基础解析的个数等于n−rn-rn−r
dimR(A)=rankA=rdimR(A)= rankA=rdimR(A)=rankA=rAX这个向量，可以看成A每一列的线性组合，所以A所有列的极大线性无关组就可以构成R(A)的基AX这个向量，可以看成A每一列的线性组合，所以A所有列的极大线性无关组就可以构成R(A)的基AX这个向量，可以看成A每一列的线性组合，所以A所有列的极大线性无关组就可以构成R(A)的基。

设{α1,α2,...,αr}\{\alpha_1,\alpha_2,...,\alpha_r\}{α1,α2,...,αr}是线性空间VVV的一向量组，记span{α1,α2,...,αr}={α=∑i=1rkiαi∣k1,k2,...,kr∈F}span\{\alpha_1,\alpha_2,...,\alpha_r\}=\{\alpha=\sum_{i=1}^rk_i\alpha_i|k_1,k_2,...,k_r\in F\}span{α1,α2,...,αr}={α=i=1∑rkiαi∣k1,k2,...,kr∈F}则span{α1,α2,...,αr}span\{\alpha_1,\alpha_2,...,\alpha_r\}span{α1,α2,...,αr}是VVV的子空间，称为由{α1,α2,...,αr}\{\alpha_1,\alpha_2,...,\alpha_r\}{α1,α2,...,αr}张成的子空间。
即把{α1,α2,...,αr}\{\alpha_1,\alpha_2,...,\alpha_r\}{α1,α2,...,αr}所有的线性组合形成的向量放在一起，形成的集合。解决了抽象线性空间中子集(即子空间)的描述。

注：

若{α1,α2,...,αm}\{\alpha_1,\alpha_2,...,\alpha_m\}{α1,α2,...,αm}是子空间WWW的基，则有W=span{α1,α2,...,αm}W=span\{\alpha_1,\alpha_2,...,\alpha_m\}W=span{α1,α2,...,αm} 设A∈Rm×nA\in \mathbb{R}^{m\times n}A∈Rm×n,记A=[A1,A−2,...,An]A=[A_1,A-2,...,A_n]A=[A1,A−2,...,An],其中Ai∈Rm,i=1,2,...,nA_i\in \mathbb{R}^m,i=1,2,...,nAi∈Rm,i=1,2,...,n.则有R(A)={Ax∣x∈Rn}=span{A1,A2,...,An}R(A)=\{Ax|x\in\mathbb{R}^n\}=span\{A_1,A_2,...,A_n\}R(A)={Ax∣x∈Rn}=span{A1,A2,...,An}

例题：

在这里插入图片描述

C 基扩张定理

定理1 设4{α1,α2,...,αr}\{\alpha_1,\alpha_2,...,\alpha_r\}{α1,α2,...,αr}是VnV^nVn中一组线性无关向量，则存在VnV^nVn中n−rn-rn−r个向量αr+1,αr+2,...,αn\alpha_{r+1},\alpha_{r+2},...,\alpha{n}αr+1,αr+2,...,αn,使得{α1,α2,...,αr,αr+1,αr+2,...,αn}\{\alpha_1,\alpha_2,...,\alpha_r,\alpha_{r+1},\alpha_{r+2},...,\alpha_n\}{α1,α2,...,αr,αr+1,αr+2,...,αn}构成VnV^nVn的基。
在这里插入图片描述

D 和空间与交空间

设W1W_1W1和W2W_2W2均是线性空间VnV^nVn的子空间

W1⋃W2W_1\bigcup W_2W1⋃W2不是线性空间VnV^nVn的子空间。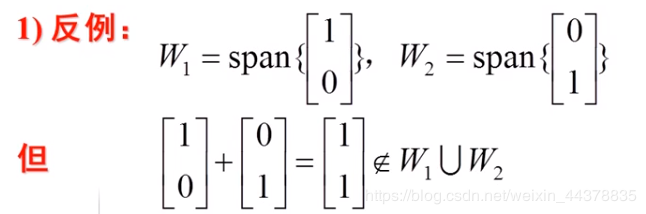
在这里插入图片描述

由定义1，对加法不封闭。

W1⋂W2W_1\bigcap W_2W1⋂W2是仍然是线性空间VnV^nVn的子空间。
在这里插入图片描述

定义2（和空间和交空间）：设W1W_1W1与W2W_2W2是线性空间VVV的两个子空间，令W1⋂W2={α∈V∣α∈W1且α∈W2}W_1\bigcap W_2=\{\alpha \in V | \alpha\in W_1且 \alpha\in W_2\}W1⋂W2={α∈V∣α∈W1且α∈W2} W1+W2={α∈V∣α=α1+α2,α1∈W1,α2∈W2}W_1+W_2=\{\alpha\in V| \alpha=\alpha_1+\alpha_2, \alpha_1\in W_1,\alpha_2\in W_2\}W1+W2={α∈V∣α=α1+α2,α1∈W1,α2∈W2}
称W1⋂W2W_1\bigcap W_2W1⋂W2为W1W_1W1与W2W_2W2的交空间。
称W1+W2W_1+W_2W1+W2为W1W_1W1与W2W_2W2的和空间。

注：

W1+W2是V的子空间W_1+W_2是V的子空间W1+W2是V的子空间；设W1=span{α1,...,αr,β1,...,βm}W_1=span\{\alpha_1,...,\alpha_r,\beta_1,...,\beta_m\}W1=span{α1,...,αr,β1,...,βm}

定理2（维数公式)设W1W_1W1与W2W_2W2是线性空间VVV的两个子空间，则有：dim(W1+W2)+dim(W1⋂W2)=dim(W1)+dim(W2)dim(W_1+W_2)+dim(W_1\bigcap W_2) =dim(W_1)+dim(W_2)dim(W1+W2)+dim(W1⋂W2)=dim(W1)+dim(W2)
在这里插入图片描述

例题：
在这里插入图片描述修改：[−5,2,3,7]>>[−5,2,3,4]T[-5,2,3,7]>>[-5,2,3,4]^T[−5,2,3,7]>>[−5,2,3,4]T

和空间W1+W2W_1+W_2W1+W2中的向量一定可以分解成两个向量之和，其中一个向量属于W1W_1W1,另一个输入W2W_2W2,即∀ξ∈W1+W2,∃α1∈W1，α2∈W1\forall\xi\in W_1+W_2,\exists \alpha_1\in W_1，\alpha_2\in W_1∀ξ∈W1+W2,∃α1∈W1，α2∈W1s.t.ξ=α1+α2s.t. \xi=\alpha_1+\alpha_2s.t.ξ=α1+α2

例子：

E 直和

定义3（直和）设W1+W2W_1+W_2W1+W2中的任一向量只能唯一地分解为W1W_1W1中的一个向量与W2W_2W2中的一个向量之和，则称W1+W2W_1+W_2W1+W2为W1W_1W1与W2W_2W2的直和，记为：W1⊕W2W_1\oplus W_2W1⊕W2.

定理3（直和等价条件）：

1)W1+W2=W1⊕W2W_1+W_2=W_1\oplus W_2W1+W2=W1⊕W2 2)W1⋂W2={0}W_1\bigcap W_2=\{0\}W1⋂W2={0} 3)dim(W1+W2)=dim(W1)+dim(W2)dim(W_1+W_2)=dim(W_1)+dim(W_2)dim(W1+W2)=dim(W1)+dim(W2) 4)0=α1+α2,α1∈W1,α2∈W2,则有α1=0,α2=00=\alpha_1 + \alpha_2,\alpha_1\in W_1,\alpha_2\in W_2,则有\alpha_1=0,\alpha_2=00=α1+α2,α1∈W1,α2∈W2,则有α1=0,α2=0.
在这里插入图片描述