Python用scipy生成特殊矩阵
目录
循环矩阵
汉克尔矩阵
费德勒矩阵
阿达马矩阵
莱斯利矩阵
希尔伯特及其逆矩阵
帕斯卡及其逆矩阵
scipy.linalg中提供了一系列特殊矩阵的生成方法,包括循环矩阵、汉克尔矩阵、费德勒矩阵、阿达马矩阵、莱斯利矩阵、希尔伯特及其逆矩阵、帕斯卡及其逆矩阵等。

A = circulant([1,2,3])
print(A)
'''
[[1 3 2]
[2 1 3]
[3 2 1]]
'''
汉克尔矩阵
汉克尔矩阵和循环矩阵十分相似,不过在向左移位的过程中,hankel(c, r=None)在末尾直接赋0。若r不为None,则通过r对末位进行赋值
print(hankel([1,2,3,4], [0,7,7,8,9]))
'''
[[1 2 3 4 7]
[2 3 4 7 7]
[3 4 7 7 8]
[4 7 7 8 9]]
'''
费德勒矩阵

阿达马矩阵的每个元素都是± 1 \pm1±1,每行都互相正交,常用于纠错码。在scipy.linalg中,hadamard(n, dtype)根据n来生成标准的n × n n\times nn×n阿达马矩阵,需要注意n nn必须为偶数,dtype为可选参数,用于指明矩阵的数据类型。
print(hadamard(4))
'''
[[ 1 1 1 1]
[ 1 -1 1 -1]
[ 1 1 -1 -1]
[ 1 -1 -1 1]]
'''
莱斯利矩阵
leslie(f, s),其输入f ff和s ss两个向量,输出矩阵的形式为

print(leslie([0.1, 2.0, 1.0, 0.1], [0.2, 0.8, 0.7]))
'''
[[0.1 2. 1. 0.1]
[0.2 0. 0. 0. ]
[0. 0.8 0. 0. ]
[0. 0. 0.7 0. ]]
'''
希尔伯特及其逆矩阵
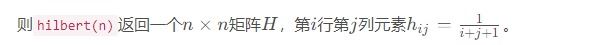
print(hilbert(3))
'''
[[1. 0.5 0.33333333]
[0.5 0.33333333 0.25 ]
[0.33333333 0.25 0.2 ]]
'''
invhilbert(n, exact=False)可生成n × n n\times nn×n希尔伯特矩阵的逆矩阵,当exact为False时,返回np.float64类型矩阵;否则返回np.int64类型。
帕斯卡及其逆矩阵
print(pascal(4))
'''
[[ 1 1 1 1]
[ 1 2 3 4]
[ 1 3 6 10]
[ 1 4 10 20]]
'''
invpascal可生成逆帕斯卡矩阵,其参数与pascal相同。
到此这篇关于Python用scipy生成特殊矩阵的文章就介绍到这了,更多相关Python scipy生成矩阵内容请搜索软件开发网以前的文章或继续浏览下面的相关文章希望大家以后多多支持软件开发网!