子空间的投影矩阵推导过程及其性质

一维投影

设向量 bbb 在子空间 aaa 上的投影为 向量 p=xap = xap=xa，则向量b 与 向量p 之间的最小误差 e=b−pe=b-pe=b−p与子空间aaa正交。

由正交的定义有： aT(b−p)=0→aT(b−xa)=0a^T(b-p)=0 \rightarrow a^T(b-xa)=0aT(b−p)=0→aT(b−xa)=0

所以：aTax=aTba^Tax=a^TbaTax=aTb

所以：x=aTbaTa=a⋅ba⋅ax = \frac{a^Tb}{a^Ta} = \frac{a \cdot b}{a \cdot a}x=aTaaTb​=a⋅aa⋅b​

向量b 在子空间 a上的投影 p=ax=aaTbaTap=ax =a\frac{a^Tb}{a^Ta}p=ax=aaTaaTb​

上式也可写成：p=aaTaTabp=\frac{aa^T}{a^Ta}bp=aTaaaT​b

其中 aaTaTa\frac{aa^T}{a^Ta}aTaaaT​ 称为子空间 a 的投影矩阵 PPP。

注意到 aaTaa^TaaT 是一个矩阵，aTaa^TaaTa 是一个数字，所以两者相除，得到的是一个矩阵

投影矩阵 PPP 的性质：

PPP 是对称矩阵，即 PT=PP^T =PPT=P 投影两次，不会改变投影结果，即 P2=PP^2=PP2=P 二维投影 投影的意义：对于方程组 Ax=bAx =bAx=b，如果 bbb 不在 矩阵AAA 的列空间中，则方程组无精确解，这时可以通过将 b 投影到AAA的列空间C(A)C(A)C(A)得到 ppp，然后求解 Ax^=pA\hat{x}=pAx^=p 来得到近似解。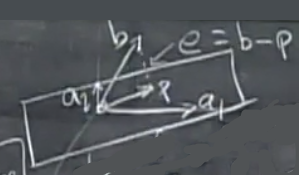

a1a_1a1​和 a2a_2a2​ 是矩阵 A 的列空间的基，ppp 是 bbb 在 A的列空间的投影，eee 是 bbb 垂直于A的列空间的分量。

所以 p=x1^a1+x2^a2=Ax^p=\hat{x_1}a_1+\hat{x_2}a_2 = A\hat{x}p=x1​^​a1​+x2​^​a2​=Ax^， x^\hat{x}x^ 是我们需要求的目标。

e=b−pe=b-pe=b−p，表示bbb的实际值与近似值ppp之间的误差，当 eee 垂直于AAA的列空间时，这个误差最小，此时求解得到的解即为最优解

因为 e=b−p=b−Ax^e = b - p = b - A\hat{x}e=b−p=b−Ax^ 垂直于 A的列空间，所以 eee 分别与 A 的基 a1a_1a1​ 和 a2a_2a2​ 垂直

所以有 a1Te=0a_1^Te=0a1T​e=0，a2Te=0a_2^Te=0a2T​e=0

即：[a1Ta2T]e=AT(b−Ax^)=ATb−ATAx^=0→ATAx^=ATb\begin{bmatrix}a_1^T \\a_2^T \end{bmatrix}e=A^T(b-A\hat{x})=A^Tb-A^TA\hat{x}=0 \rightarrow A^TA\hat{x}=A^Tb[a1T​a2T​​]e=AT(b−Ax^)=ATb−ATAx^=0→ATAx^=ATb

所以 x^=(ATA)−1ATb\hat{x}=(A^TA)^{-1}A^Tbx^=(ATA)−1ATb

又因为 p=Ax^=A(ATA)−1ATbp=A\hat{x}=A(A^TA)^{-1}A^Tbp=Ax^=A(ATA)−1ATb

ppp 是 bbb 在 A的列空间上的投影，所以A 的投影矩阵为 P=A(ATA)−1ATP=A(A^TA)^{-1}A^TP=A(ATA)−1AT

如果 A 是可逆矩阵，则有P=AA−1(AT)−1AT=IP=AA^{-1}(A^T)^{-1}A^T = IP=AA−1(AT)−1AT=I，此时 b 在 A的列空间中，b 的投影还是它自身，所以投影矩阵为 单位矩阵 III

nnn 维的投影矩阵 PPP 的性质：

PPP 是对称矩阵，即 PT=PP^T=PPT=P P2=PP^2=PP2=P

由以上讨论可得到：b=Pb+PNbb = Pb + P_Nbb=Pb+PN​b，其中 PNP_NPN​ 是垂直于矩阵 A 的法向量，于是有 Ib=Pb+Pnb→I=P+PN→P=I−PNIb = Pb + P_nb \rightarrow I = P+P_N \rightarrow P=I-P_NIb=Pb+Pn​b→I=P+PN​→P=I−PN​。所以可以通过求解法向量的投影矩阵，间接得到 矩阵A 的投影矩阵。

作者：Linky1990

子空间 矩阵